概率分佈一覽

以下係常用嘅概率分佈同相關概念一覽。

概率分佈（probability distribution）係指一個表明某個變數每個可能數值出現嘅機會率嘅函數，

\Pr(X=x)=f(x)

當中 $f$ 就係個概率分佈；呢個函數可以畫做一個表，X 軸代表個目標變數嘅數值，Y 軸代表嗰個目標變數嘅每個數值出現嘅機率；是但搵個變數 $X$ ， $X$ 喺總體當中有一個概率分佈，表示 $X$ 每個可能數值 $x$ 出現嘅機率，呢個分佈喺實際上係不可知嘅，研究者淨係有得攞樣本，量度樣本當中嘅概率分佈（喺個樣本入面， $X$ 嘅每個可能數值出現嘅機率大約係幾多），靠噉嚟估計個總體嘅分佈^[1]。

喺廿一世紀統計學上，比較常用嘅概率分佈有以下呢啲：

離散概率分佈

離散概率分佈（discrete probability distribution）：指所描述嘅變數 $X$ 嘅可能數值係離散嘅概率分佈^[2]。

概率質量函數（probability mass function，PMF）：描述一個離散概率分佈嘅函數；一個離散概率分佈嘅 PMF 會講明嗰個概率分佈嘅每一個離散可能數值出現嘅機會率^[2]：
$\sum p_{X}(x_{i})=1$ ，啲可能性嘅機率冚唪唥加埋係 1；

$p(x_{i})>0$ ，每個可能性嘅機率大過 0；

$p(x)=0{\text{ for all other x}}$ ，啲可能性以外嘅數值出現嘅機會率係 0。

一個概率質量函數； $X$ 嘅可能數值得三個（1、3 同 7），每個數值都掕住咗個「出現嘅機率」，而呢啲機率加埋係 1。

離散均勻分佈（discrete uniform distribution）：每個可能離散數值出現嘅機率都一樣，概率質量函數係^[2]：
$f(x)={\frac {1}{n}}$ ，當中 $n$ 係 $X$ 有幾多個可能數值。
伯努利分佈（Bernoulli distribution）：描述嘅變數 $k$ $k$ 得兩個可能數值，數值係 1 嘅機會率係 $p$ $p$ ，數值係 0 嘅機會率係 $q=(1-p)$ $q=(1-p)$ ，概率質量函數 $f(k;p)$ $f(k;p)$ 係^[3]：
$f(k;p)={\begin{cases}p&{\text{if }}k=1,\\q=1-p&{\text{if }}k=0.\end{cases}}$
- 廣義伯努利分佈（generalized Bernoulli distribution / multinoulli distribution）：描述嘅變數 $k$ 有 $n$ 個離散可能數值，概率質量函數係^[4]：
  $f(i)={\begin{cases}p_{1}&{\text{if }}i=1,\\p_{2}&{\text{if }}i=2,\\p_{3}&{\text{if }}i=3,\\...\end{cases}}$

二項分佈（binomial distribution）：描述 $n$ $n$ 次結果二元嘅試驗；想像有個結果係二元－得兩個可能結果（1 同 0）－嘅試驗，例如掟銀仔，做 $n$ $n$ 咁多次，每次試驗嘅結果都有 $p$ $p$ 咁多機會率係 1， $q=(1-p)$ $q=(1-p)$ 咁多機會率係 0，而每次試驗嘅結果都係獨立嘅（一次試驗嘅結果唔受其他試驗嘅結果影響）。概率質量函數 $f(k,n,p)$ $f(k,n,p)$ ，即係得出 $k$ $k$ 咁多個 1 嘅機會率係^[3]：
$f(k,n,p)=\Pr(k;n,p)=\Pr(X=k)={\binom {n}{k}}p^{k}(1-p)^{n-k}$
- 多項分佈（multinomial distribution）：係二項分佈嘅廣義化，描述嘅試驗有 $k$ 個可能結果，做 $n$ 咁多次（想像掟一粒 $k$ 面嘅骰仔掟 $n$ 咁多次）。概率質量函數係^[5]：
  $f(k,n,p)={\frac {n!}{x_{1}!\cdots x_{k}!}}p_{1}^{x_{1}}\cdots p_{k}^{x_{k}}$

幾何分佈（geometric distribution）：可以指兩個唔同嘅概率分佈，兩者都涉及一個結果二元嘅試驗^[6]：
- 做咗個試驗 $k$ 次，終於得到 1 次陽性結果，而之前嗰啲試驗結果冚唪唥都係陰性：
  $\Pr(X=k)=(1-p)^{k-1}p$
  
  ${\text{for }}k=1,2,3,...$
- $k$ 代表要做幾多次陰性試驗，先可以得到一次陽性結果：
  $\Pr(Y=k)=(1-p)^{k}p$
  
  ${\text{for }}k=0,1,2,3,...$

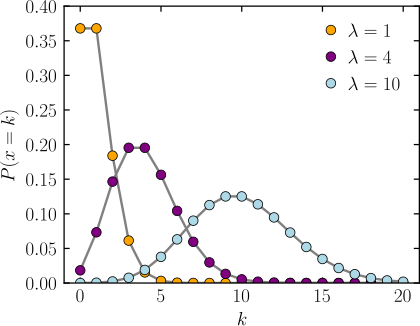
撥桑分佈（Poisson distribution）：模擬嘅事件有已知嘅平均發生率，而每件事件嘅發生彼此之間獨立，發生嘅次數設做 $k$ ，概率質量函數係^[7]：
$\!f(k;\lambda )=\Pr(X=k)={\frac {\lambda ^{k}e^{-\lambda }}{k!}}$ ，當中 $\lambda$ 係預期會發生嘅次數（唔一定係整數）。

連續概率分佈

連續概率分佈（continuous probability distribution）：指所描述嘅變數 $X$ 嘅可能數值係連續嘅^[2]。

概率密度函數（probability density function，PDF）：描述一個連續概率分佈嘅函數；一個連續概率分佈嘅 PDF 會講明嗰個概率分佈嘅每一個可能數值出現嘅機會率大約係幾多^[2]，
$\Pr(X=x)=f(x)$ 。
均勻分佈（continuous uniform distribution，簡稱 uniform distribution）：喺 $a$ （最細可能數值）同 $b$ （最大可能數值）之間嘅每個可能數值 $x$ 出現嘅機會率都一樣，概率密度函數係^[2]：
${\begin{cases}{\frac {1}{b-a}}&{\text{for}}\ a\leq x\leq b,\\0&{\text{otherwise}}.\end{cases}}$
常態分佈（normal distribution）：統計分析上最常用嘅概率分佈之一；喺常態分佈下，出現得最頻密嘅數值會係個平均數 $\mu$ ，而離平均數愈遠嘅數值就愈少會出現，畫做圖嘅話會出一條鐘形線（bell curve）；常見可以用常態分佈模擬嘅變數有人類嘅智商－多數人嘅智商數值都傾向於平均數，愈極端嘅數值愈少出現，即係話好少有智商極高或者極低嘅人。常態分佈個概率密度函數係（ $\sigma$ 係個分佈嘅標準差）^[1]：
$f(x)={\frac {1}{\sigma {\sqrt {2\pi }}}}e^{-{\frac {1}{2}}\left({\frac {x-\mu }{\sigma }}\right)^{2}}$

常態分佈畫做圖嘅樣；x 軸代表目標變數嘅數值，y 軸代表目標變數嘅每個數值出現嘅機會率 $f(x)$ 。

對數正態分佈（log-normal distribution）：指一個隨機變數嘅對數呈常態分佈；如果話 $X$ 呢個隨機變數呈對數正態分佈嘅話，噉 $Y=\ln(X)$ 呈常態分佈^[8]。
$\ln(X)\sim {\mathcal {N}}(\mu ,\sigma ^{2})$ ；當中 $\mu$ 係個常態分佈嘅平均值，而 $\sigma$ 係個常態分佈嘅標準差。

其概率密度函數係： $f(x)={\frac {1}{x\sigma {\sqrt {2\pi }}}}\ \exp \left(-{\frac {\left(\ln x-\mu \right)^{2}}{2\sigma ^{2}}}\right)$ ^[8]
柏里圖分佈（Pareto distribution）：常用嚟模擬人口隨時間增長嘅一個概率分佈^[9]，概率密度函數如下^[10]：
$f_{X}(x)={\begin{cases}{\frac {\alpha x_{\mathrm {m} }^{\alpha }}{x^{\alpha +1}}}&x\geq x_{\mathrm {m} },\\0&x<x_{\mathrm {m} }.\end{cases}}$

當中 $x_{\mathrm {m} }$ 係指 $X$ 嘅最細可能數值，而 $\alpha$ 係一個正嘅參數。

柏里圖分佈嘅 PDF 畫做圖嘅樣；當中 $x_{\mathrm {m} }=1$ ，而圖入面唔同嘅線代表唔同 $\alpha$ 數值下嘅 PDF。

指數分佈（exponential distribution）：喺物理學上係常用嚟模擬一啲慢慢衰減嘅物理量嘅函數，例如係核衰變噉；喺統計學上，呢個函數可以用嚟模擬一啲機會率（ $\Pr(X=x)$ ）會隨住時間（ $t$ ）過去慢慢下降嘅事件，指數分佈嘅概率密度函數如下^[11]：
$f(x;\lambda )={\begin{cases}\lambda e^{-\lambda x}&x\geq 0,\\0&x<0.\end{cases}}$

指數分佈嘅 PDF 畫做圖嘅樣；圖入面唔同嘅線代表唔同 $\lambda$ 數值下嘅 PDF。

分佈概念

頻率分佈（frequency distribution）：描述一個樣本入面每個可能數值出現咗幾多次嘅表^[12]。例：

身高間距	頻率	累計頻率
< 5.0 呎	25	25
5.0 - 5.5 呎	35	60
5.5 - 6.0 呎	20	80
6.0 - 6.5 呎	20	100

累計函數（cumulative distribution function）：描述一個概率分佈之下 $X$ $X$ 嘅累計值會點隨 $x$ $x$ 變化嘅函數 $c(x)$ $c(x)$ ； $c(x_{0})$ $c(x_{0})$ 表示「由個樣本嗰度隨機抽一個個體，個個體嘅 $x$ $x$ （叫呢個值做 $x_{d}$ $x_{d}$ ）細過或者等如 $x_{0}$ $x_{0}$ 」嘅機會率，
$c(x_{0})=\Pr(x_{d}\leq x_{0})$
- 無論連續定離散嘅概率分佈都可以有相應嘅累計函數^[13]。

對稱度（symmetry）：一個概率分佈可以有嘅一個屬性，攞個概率分佈當中嘅一個 $x$ $x$ 值，個分佈喺 $x$ $x$ 左邊嗰部份同個分佈喺 $x$ $x$ 右邊嗰部份形狀上愈相似，個概率分佈以 $x$ $x$ 為中心嘅對稱度就愈高；喺實際應用上，量度一個概率分佈嘅對稱度嗰陣會用嘅 $x$ $x$ 值通常會係個分佈嘅平均值^[14]。
- 對稱概率分佈（symmetric probability distribution）：一個對稱概率分佈定義上係指符合下面呢條式嘅概率分佈，當中 $x_{m}$ 係個分佈上嘅一點^[14]：
  $f(x_{m}-\delta )=f(x_{m}+\delta )$ ${\text{for}}$ 所有實數 $\delta$
動差（moment）：泛指描述一個函數（例如概率分佈）嘅形狀嘅指標數值^[15]。
- 偏度（skewness）：指個分佈有幾「歪埋一邊」；要評估一個分佈嘅偏度，一條可能嘅式如下：
  ${\tilde {\mu }}_{3}=\operatorname {E} \left[\left({\frac {X_{i}-\mu }{\sigma }}\right)^{3}\right]$ ；
  - 當中 $X$ 係第 $i$ 個個案嘅 $x$ 值， $\mu$ 係個分佈嘅平均值，而 $\sigma$ 係個分佈嘅標準差；呢個數值愈大，表示個分佈偏度愈高^[16]。
- 峰度（kurtosis）：指個分佈有幾「扁」；要評估一個分佈嘅偏度，一條可能嘅式如下：
  $\operatorname {Kurt} [X]=\operatorname {E} \left[\left({\frac {X-\mu }{\sigma }}\right)^{4}\right]$ ；
  - 當中 $X$ 係第 $i$ 個個案嘅 $x$ 值， $\mu$ 係個分佈嘅平均值，而 $\sigma$ 係個分佈嘅標準差；呢個數值愈大，表示個分佈愈扁，（如果係常態分佈）比例上有愈多嘅個案處於極端值^[16]。

抽樣分佈（sampling distribution）：攞一個基於隨機抽樣嘅統計量，個統計量嘅概率分佈就係佢個抽樣分佈^[17]。
- 標準誤差（standard error）：一個統計量嘅標準誤差係指佢抽樣分佈嘅標準差（SD）^[17]。
聯合概率分佈（joint probability distribution）：一個聯合概率分佈同時描述緊多過一個變數嘅分佈；一個兩變數聯合概率分佈會有打橫嘅 X 軸 Y 軸以及打戙嘅 Z 軸，總共三條軸，X 軸 Y 軸分別描述嗰兩個變數 $X$ 同 $Y$ 嘅數值，而 X 軸同 Y 軸成嘅平面當中每一點嘅高度（Z 值）反映咗「 $X$ 係呢個數值而且同時 $Y$ 係呢個數值」嘅機會率。當變數有多過兩個嗰陣同一道理^[18]。

獨立同分佈（independent and identically distributed，iid）：係概率論同統計學上嘅一個概念；如果話一柞隨機性變數（或者事件）係「獨立同分佈」嘅話，意思係佢哋嘅概率分佈完全一樣（每次抽嗰陣個結果嘅概率分佈一樣），而且彼此之間獨立（抽一次嘅結果唔會受打前抽到嘅數值影響）^[19]。
中央極限定理（central limit theorem，CLT）：概率論同統計學上最重要嘅定理之一；根據 CLT，想像有個變數 $x$ $x$ ，只要三條條件成立：
1. 個總體喺 $x$ 上嘅變異數係有限，
2. 每次抽樣都係獨立同分佈（iid）嘅，
3. 而且個樣本夠大，
- 如果呢三條條件成立，噉無論個總體喺 $x$ 上嘅概率分佈係點嘅樣，而家做抽樣，個樣本喺 $x$ 上嘅平均值嘅分佈會接近一個常態分佈^[19]。

唔同 $n$ 同 $p$ ^{[註 1]}值嘅二項分佈出嘅樣本平均值嘅分佈；
綠線：理論上嘅常態分佈（用嚟做對照）；
紅線：嗰個 $n$ 同 $p$ 值組合出嘅樣本平均值分佈。

註釋

↑ $p$ 係二項分佈當中有嘅一個參數。

睇埋

概率同統計學詞彙表

攷

↑ ^1.0 ^1.1 Ash, Robert B. (2008). Basic probability theory (Dover ed.). Mineola, N.Y.: Dover Publications. pp. 66–69.
↑ ^2.0 ^2.1 ^2.2 ^2.3 ^2.4 ^2.5 1941-, Çınlar, E. (Erhan) (2011). Probability and stochastics. New York: Springer. p. 51.
↑ ^3.0 ^3.1 Bertsekas, Dimitri P. (2002). Introduction to Probability. Tsitsiklis, John N., Τσιτσικλής, Γιάννης Ν. Belmont, Mass.: Athena Scientific.
↑ Murphy, K. P. (2012). Machine learning: a probabilistic perspective, p. 35. MIT press.
↑ Ostrovski, Vladimir (May 2017). "Testing equivalence of multinomial distributions". Statistics & Probability Letters. 124: 77–82.
↑ Gallager, R.; van Voorhis, D. (March 1975). "Optimal source codes for geometrically distributed integer alphabets (Corresp.)". IEEE Transactions on Information Theory. 21 (2): 228–230.
↑ Haight, Frank A. (1967), Handbook of the Poisson Distribution, New York, NY, USA: John Wiley & Sons.
↑ ^8.0 ^8.1 Johnson, Norman L.; Kotz, Samuel; Balakrishnan, N. (1994), "14: Lognormal Distributions", Continuous univariate distributions. Vol. 1, Wiley Series in Probability and Mathematical Statistics: Applied Probability and Statistics (2nd ed.), New York: John Wiley & Sons.
↑ Reed, William J.; et al. (2004). "The Double Pareto-Lognormal Distribution – A New Parametric Model for Size Distributions". Communications in Statistics – Theory and Methods. 33 (8): 1733–53.
↑ VAN MONTFORT, M.A.J. (1986). "The Generalized Pareto distribution applied to rainfall depths". Hydrological Sciences Journal. 31 (2): 151–162.
↑ Elfessi, Abdulaziz; Reineke, David M. (2001). "A Bayesian Look at Classical Estimation: The Exponential Distribution". Journal of Statistics Education. 9 (1).
↑ Manikandan, S (1 January 2011). "Frequency distribution". Journal of Pharmacology & Pharmacotherapeutics. 2 (1): 54–55.
↑ Deisenroth,Faisal,Ong, Marc Peter,A Aldo, Cheng Soon (2019). Mathematics for Machine Learning. Cambridge University Press. p. 181.
↑ ^14.0 ^14.1 Ali, Mir M. (1980). "Characterization of the Normal Distribution Among the Continuous Symmetric Spherical Class". Journal of the Royal Statistical Society. Series B (Methodological). 42 (2): 162–164.
↑ Spanos, Aris (1999). Probability Theory and Statistical Inference. New York: Cambridge University Press. pp. 109–130.
↑ ^16.0 ^16.1 MacGillivray, HL (1992). "Shape properties of the g- and h- and Johnson families". Communications in Statistics - Theory and Methods. 21: 1244–1250.
↑ ^17.0 ^17.1 Altman, Douglas G; Bland, J Martin (2005-10-15). "Standard deviations and standard errors". BMJ: British Medical Journal. 331 (7521): 903.
↑ Hazewinkel, Michiel, ed. (2001) [1994], "Joint distribution", Encyclopedia of Mathematics, Springer Science+Business Media B.V. / Kluwer Academic Publishers.
↑ ^19.0 ^19.1 Dinov, Ivo; Christou, Nicolas; Sanchez, Juana (2008). "Central Limit Theorem: New SOCR Applet and Demonstration Activity". Journal of Statistics Education. ASA. 16 (2).

[20] $p$ 係二項分佈當中有嘅一個參數。

[robert2008-1] 1.0 ^1.1 Ash, Robert B. (2008). Basic probability theory (Dover ed.). Mineola, N.Y.: Dover Publications. pp. 66–69.

[1941cnlar-2] 2.0 ^2.1 ^2.2 ^2.3 ^2.4 ^2.5 1941-, Çınlar, E. (Erhan) (2011). Probability and stochastics. New York: Springer. p. 51.

[bertsekas2002-3] 3.0 ^3.1 Bertsekas, Dimitri P. (2002). Introduction to Probability. Tsitsiklis, John N., Τσιτσικλής, Γιάννης Ν. Belmont, Mass.: Athena Scientific.

[4] Murphy, K. P. (2012). Machine learning: a probabilistic perspective, p. 35. MIT press.

[5] Ostrovski, Vladimir (May 2017). "Testing equivalence of multinomial distributions". Statistics & Probability Letters. 124: 77–82.

[6] Gallager, R.; van Voorhis, D. (March 1975). "Optimal source codes for geometrically distributed integer alphabets (Corresp.)". IEEE Transactions on Information Theory. 21 (2): 228–230.

[7] Haight, Frank A. (1967), Handbook of the Poisson Distribution, New York, NY, USA: John Wiley & Sons.

[johnson1994-8] 8.0 ^8.1 Johnson, Norman L.; Kotz, Samuel; Balakrishnan, N. (1994), "14: Lognormal Distributions", Continuous univariate distributions. Vol. 1, Wiley Series in Probability and Mathematical Statistics: Applied Probability and Statistics (2nd ed.), New York: John Wiley & Sons.

[9] Reed, William J.; et al. (2004). "The Double Pareto-Lognormal Distribution – A New Parametric Model for Size Distributions". Communications in Statistics – Theory and Methods. 33 (8): 1733–53.

[10] VAN MONTFORT, M.A.J. (1986). "The Generalized Pareto distribution applied to rainfall depths". Hydrological Sciences Journal. 31 (2): 151–162.

[11] Elfessi, Abdulaziz; Reineke, David M. (2001). "A Bayesian Look at Classical Estimation: The Exponential Distribution". Journal of Statistics Education. 9 (1).

[12] Manikandan, S (1 January 2011). "Frequency distribution". Journal of Pharmacology & Pharmacotherapeutics. 2 (1): 54–55.

[13] Deisenroth,Faisal,Ong, Marc Peter,A Aldo, Cheng Soon (2019). Mathematics for Machine Learning. Cambridge University Press. p. 181.

[ali1980-14] 14.0 ^14.1 Ali, Mir M. (1980). "Characterization of the Normal Distribution Among the Continuous Symmetric Spherical Class". Journal of the Royal Statistical Society. Series B (Methodological). 42 (2): 162–164.

[15] Spanos, Aris (1999). Probability Theory and Statistical Inference. New York: Cambridge University Press. pp. 109–130.

[macgill1992-16] 16.0 ^16.1 MacGillivray, HL (1992). "Shape properties of the g- and h- and Johnson families". Communications in Statistics - Theory and Methods. 21: 1244–1250.

[altman2005-17] 17.0 ^17.1 Altman, Douglas G; Bland, J Martin (2005-10-15). "Standard deviations and standard errors". BMJ: British Medical Journal. 331 (7521): 903.

[18] Hazewinkel, Michiel, ed. (2001) [1994], "Joint distribution", Encyclopedia of Mathematics, Springer Science+Business Media B.V. / Kluwer Academic Publishers.

[dinov2008-19] 19.0 ^19.1 Dinov, Ivo; Christou, Nicolas; Sanchez, Juana (2008). "Central Limit Theorem: New SOCR Applet and Demonstration Activity". Journal of Statistics Education. ASA. 16 (2).

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[註 1]