Палярная сістэма каардынат

Палярная сістэма каардынат — двухмерная сістэма каардынат, у якой кожны пункт на плоскасці вызначаецца двума лікамі — палярным вуглом і палярным радыусам. Палярная сістэма каардынат асабліва карысная ў выпадках, калі адносіны паміж пунктамі прасцей адлюстраваць у выглядзе радыусаў і вуглоў; ў больш распаўсюджанай, дэкартавай або прамавугольнай сістэме каардынат, такія адносіны можна ўсталяваць толькі шляхам прымянення трыганаметрычных ураўненняў.
Палярная сістэма каардынат задаецца прамянём, які называюць нулявым або палярнай воссю. Пункт, з якога выходзіць гэты прамень, называецца пачаткам каардынат альбо полюсам. Любы пункт на плоскасці вызначаецца двума палярнымі каардынатамі: радыяльнай і вуглавой. Радыяльная каардыната (звычайна пазначаецца ) адпавядае адлегласці ад пункта да пачатку каардынат. Вуглавая каардыната таксама называецца палярным вуглом або азімутам і пазначаецца , роўная куце, на які трэба павярнуць супраць гадзінны стрэлкі палярную вось для таго, каб патрапіць у гэты пункт.[1]
Вызначаная такім чынам радыяльная каардыната можа прымаць значэнні ад нуля да бясконцасці, а вуглавая каардыната змяняецца ў межах ад 0° да 360°. Аднак, для зручнасці вобласць значэнняў палярнай каардынаты можна пашырыць за межы поўнага вугла, а таксама дазволіць ёй прымаць адмоўныя значэння, што адказвае павароту палярнай восі па гадзіннікавай стрэлцы.
Графічнае прадстаўленне
[правіць | правіць зыходнік]
Кожны пункт у палярнай сістэме каардынат можа быць вызначана двума палярнымі каардынатамі, што звычайна называюцца (радыяльная каардыната, вуглавая адлегласць, сустракаецца варыянт ) і (вуглавая каардыната, палярны вугал, азімут, пазіцыйны вугал, часам пішуць альбо ). Каардыната адпавядай адлегласці да полюса, а каардыната роўная куце ў напрамку супраць гадзінны стрэлкі ад прамяня праз 0° (часам называецца палярнай воссю)[1].
Палярны радыус вызначаны для любога пункта плоскасці і прымае неадмоўныя значэння . Палярны вугал вызначаны для любога пункта плоскасці, за выключэннем полюса , і прымае значэння . Палярны вугал вымяраецца ў радыянах і адлічваецца ад палярнай восі:
- ў дадатным напрамку (супраць напрамкі руху гадзінны стрэлкі), калі значэнне вугла станоўчае;
- у адмоўным кірунку (па кірунку руху гадзіннікавай стрэлкі), калі значэнне вугла адмоўнае.
Напрыклад, пункт з каардынатамі будзе выглядаць на графіку як пункт на промні, які ляжыць пад вуглом 60° да палярнай восі, на адлегласці 3 адзінкі ад полюса. Пункт з каардынатамі будзе намаляваная на тым жа месцы.
Камплексныя лікі
[правіць | правіць зыходнік]
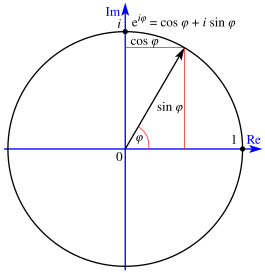
Кожны камплексны лік можа быць прадстаўлены пунктам на камплекснай плоскасці, і, адпаведна, гэты пункт можа вызначацца ў дэкартавых каардынатах (прамавугольная альбо дэкартавая форма), або ў палярных каардынатах (палярная форма). Камплексны лік z можа быць запісаны ў прамавугольнай форме як:
дзе i — уяўная адзінка, ці ў палярнай:
і адсюль, як:
дзе e — лік Эйлера. Дзякуючы формуле Эйлера, абодва прадстаўлення эквівалентныя.[2] (Варта адзначыць, што ў гэтай формуле, падобна астатнім формул, якія змяшчаюць узвядзенне ў ступень вуглоў, вугал φ зададзена ў радыянах.)
Для пераходу паміж прамавугольным і палярным прадстаўленнем камплексных лікаў, могуць выкарыстоўвацца прыведзеныя вышэй формулы пераўтварэння паміж сістэмамі каардынат.
Аперацыі множанне, дзяленне і узвядзенне ў ступень з камплекснымі лікамі, як правіла, прасцей праводзіць у палярнай форме. Згодна з правіламі ўзвядзення ў ступень:
- Множанне:
- Дзяленне:
- Узвядзенне ў ступень (формула Муавра):
Зноскі
- ↑ а б Brown, Richard G. (1997). Andrew M. Gleason (рэд.). Advanced Mathematics: Precalculus with Discrete Mathematics and Data Analysis. Evanston, Illinois: McDougal Littell. ISBN 0-395-77114-5.
- ↑
Smith, Julius O. (2003). "Euler's Identity". Mathematics of the Discrete Fourier Transform (DFT). W3K Publishing. ISBN 0-9745607-0-7.
{{cite book}}:|access-date=патрабуе|url=(даведка); Вонкавая спасылка ў|chapterurl=|chapterurl=ігнараваны (прапануецца|chapter-url=) (даведка)