Полярная система координат

Обзорная статья: Система координат

Полярные координаты

Поля́рная систе́ма координа́т (лат. polus — полюс, от др.-греч. πόλος — полюс, ось) — система координат на плоскости, определяющаяся двумя полярными координатами $\rho$ и $\varphi$, которые связаны с декартовыми прямоугольными координатами $x$ и $y$ следующими выражениями:

$x=\rho \cos \varphi ,\quad$ $y=\rho \sin \varphi ,$

где $\quad 0\leqslant \rho <+\infty ,\quad$ $0\leqslant \varphi <2\pi$.

Такие ограничения на значения полярных координат ставятся для того, чтобы соответствие между точками плоскости, отличными от полюса, и парами полярных координат $(\rho ,\varphi )$ получилось взаимно однозначным.

Полярные координаты точек плоскости

Полярные координаты — координаты произвольной точки $M$ плоскости в выбранной полярной системе координат в виде следующих двух чисел: полярный радиус $\rho$, — расстояние от полюса $O$ до точки $M$; полярный угол $\varphi$, — угол, на который поворачивается полярная ось до совмещения с точкой $M$.

В этих определениях предполагается, что полюс $O$ и точка $M$ не совпадают. Полюс $O$ находится на особом положении: его полярный радиус $\rho$ полагается равным нулю, а полярный угол $\varphi$ — неопределённым, то есть ему можно приписать любое значение (иногда приписывают значение $\varphi =0$).

Координатные линии полярной системы координат

Полярная система координат ортогональна. Ортогональные координатные линии полярной системы координат суть концентрические окружности при $\rho ={\text{const}}$ и лучи при $\varphi ={\text{const}}$.

Полярная система координат особенно проста и полезна в случаях, когда отношения между точками проще изобразить в виде радиусов и углов, тогда как в более распространённой декартовой, или прямоугольной, системе координат такие отношения можно установить только путём применения тригонометрических уравнений.

Пример 1. Как полярные координаты $\rho =3$, $\varphi =-{\frac {\pi }{2}}$, так и $\rho =3$, $\varphi ={\frac {3\pi }{2}}$ задают одну и ту же точку плоскости. Как полярные координаты $\rho =1$, $\varphi =0$, так и $\rho =1$, $\varphi =2\pi$ и $\rho =1$, $\varphi =-2\pi$ задают также одну и ту же точку плоскости.

Замечание. Часто требуется в ущерб однозначности поддерживать непрерывное изменение полярных координат точек (например, у уравнениях, описывающих кривые на плоскости). Тогда отказываются от приведённых ограничений для $\rho$ и $\varphi$. Закон изменения значений полярных координат $\rho$ и $\varphi$ выясняется в каждом конкретном случае. Обычно в качестве полярного угла берут величину $\varphi +k\pi$, где $k$ — произвольное целое число, а полярному радиусу приписывают знак плюс или минус, смотря по ситуации.

Обобщённая полярная система координат — система координат на плоскости, определяющаяся двумя обобщёнными полярными координатами $r$ и $\psi$, которые связаны с декартовыми прямоугольными координатами $x$ и $y$ следующими выражениями:

$x=ar\cos \psi ,\quad$ $y=br\sin \psi ,$

где $\quad 0\leqslant r<+\infty ,\quad$ $0\leqslant \psi <2\pi ,\quad$ $a,b>0,\quad$ $a\neq b$. Координатные линии суть эллипсы при $r={\text{const}}$ и лучи при $\psi ={\text{const}}$.

Полярную систему координат в трёхмерном пространстве представляют цилиндрическая система координат и сферическая система координат.

История

Понятие угла и радиуса были известны ещё в первом тысячелетии до нашей эры. Греческий астроном Гиппарх (190—120 до н. э.) создал таблицу, в которой для разных углов приводились длины хорд. Существуют свидетельства применения им полярных координат для определения положения небесных тел. Архимед в своём сочинении «Спирали» описывает так называемую спираль Архимеда, функцию, радиус которой зависит от угла. Работы греческих исследователей, однако, не развились в целостное определение системы координат.

В IX веке персидский математик Хаббаш аль-Хасиб (аль-Марвази́) применял методы картографических проекций и сферической тригонометрии для преобразования полярных координат в другую систему координат с центром в некоторой точке на сфере, в этом случае, для определения Киблы — направления на Мекку. Персидский астроном Абу Райхан Бируни (973—1048) выдвинул идеи, которые выглядят как описание полярной системы координат. Он был первым, кто, примерно в 1025 году, описал полярную экви-азимутальную равнопромежуточную проекцию небесной сферы.

Существуют разные версии о введении полярных координат в качестве формальной системы координат. Полная история возникновения и исследования описана в работе профессора из Гарварда Джулиан Лоувел Кулидж «Происхождение полярных координат». Грегуар де Сен-Венсан и Бонавентура Кавальери независимо друг от друга пришли к похожей концепции в середине XVII века. Сен-Венсан описал полярную систему в личных заметках в 1625 году, напечатав свои труды в 1647; а Кавальери напечатал свои труды в 1635 году, и исправленную версию в 1653 году. Кавальери применял полярные координаты для вычисления площади, ограниченной спиралью Архимеда. Блез Паскаль впоследствии использовал полярные координаты для вычисления длин параболических дуг.

В книге «Метод флюксий» (англ. Method of Fluxions, написана в 1671 году, напечатана в 1736 году) сэр Исаак Ньютон исследовал преобразование между полярными координатами, которые он обозначал как «Седьмой способ; Для спиралей» («англ. Seventh Manner; For Spirals»), и девятью другими системами координат. В статье, опубликованной в 1691 году в журнале Acta eruditorum, Якоб Бернулли использовал систему с точкой на прямой, которые он назвал полюсом и полярной осью соответственно. Координаты задавались как расстояние от полюса и угол от полярной оси. Работа Бернулли была посвящена проблеме нахождения радиуса кривизны кривых, определённых в этой системе координат.

Введение термина «полярные координаты» приписывают Грегорио Фонтана. В XVIII веке он входил в лексикон итальянских авторов. В английский язык термин попал через перевод трактата Сильвестра Лакруа «Дифференциальное и интегральное исчисление», выполненного в 1816 году Джорджем Пикоком Для трёхмерного пространства полярные координаты впервые предложил Алекси Клеро, а Леонард Эйлер был первым, кто разработал соответствующую систему.

Определение полярной системы координат

Полярная система координат

Поля́рная систе́ма координа́т (лат. polus — полюс, от др.-греч. πόλος — полюс, ось) — система координат на плоскости, которую определяют следующие пять объектоа:

• масштаб, то есть единица измерения длины;
• единица измерения плоских углов (обычно радиан);
• ориентация плоскости, то есть направление её вращения, которое выбрано положительным (обычно против часовой стрелки);
• фиксированная точка плоскости $O$. Эта точка называется началом, или полюсом, системы координат;
• луч $Ox$, исходящий из точки $O$ и от неё направленный (обычно горизонтальный). Этот луч называется полярной осью.

Полярные координаты точек плоскости

Полярные координаты — координаты произвольной точки $M$ плоскости в выбранной полярной системе координат в виде следующих двух чисел:

• первая полярная координата, или полярный радиус $\rho$, — расстояние от полюса $O$ до точки $M$;
• вторая полярная координата, или полярный угол $\varphi$, — угол, на который поворачивается полярная ось до совмещения с точкой $M$.

Точка $M$, имеющая полярные координаты, обозначаемые греческими буквами $\rho$ и $\varphi$, записываетсчя символом $M(\rho ,\varphi )$ (иногда $M\langle \varphi ,r\rangle$).

В этих определениях предполагается, что полюс $O$ и точка $M$ не совпадают. Полюс $O$ находится на особом положении: его полярный радиус $\rho$ полагается равным нулю, а полярный угол $\varphi$ — неопределённым, то есть ему можно приписать любое значение (иногда приписывают значение $\varphi =0$).

Замечание. Раньше первой полярной координатой могли называть полярный угол $\varphi$, а второй — полярный радиус $\rho$. Полярный радиус также могут обозначать латинской буквой $r$, а полярный угол $\varphi$ могут называть амплитудой, или фазой, и обозначать $\theta$.

Координатные линии полярной системы координат

Полярная система координат ортогональна. Ортогональные координатные линии полярной системы координат суть концентрические окружности при $\rho ={\text{const}}$ и лучи при $\varphi ={\text{const}}$.

Полярная система координат особенно проста и полезна в случаях, когда отношения между точками проще изобразить в виде радиусов и углов, тогда как в более распространённой декартовой, или прямоугольной, системе координат такие отношения можно установить только путём применения тригонометрических уравнений.

Пример 1. Как полярные координаты $\rho =3$, $\varphi =-{\frac {\pi }{2}}$, так и $\rho =3$, $\varphi ={\frac {3\pi }{2}}$ задают одну и ту же точку плоскости. Как полярные координаты $\rho =1$, $\varphi =0$, так и $\rho =1$, $\varphi =2\pi$ и $\rho =1$, $\varphi =-2\pi$ задают также одну и ту же точку плоскости.

Каждой паре значений полярных координат $\rho$ и $\varphi$ соответствует только одна точка плоскости, но одной и той же точке плоскости $M$ соответствует бесконечное множество значений полярного угла $\varphi$, отличающихся друг от друга на число, кратное $2\pi$ (см. пример 1).

Как правило, полагают, что значения полярных координат $\rho$ и $\varphi$ точек плоскости, отличных от полюса, лежат в следующих границах:

$0<\rho <+\infty ,\quad$ $0\leqslant \varphi <2\pi$

(иногда $\quad 0<\rho <+\infty ,\quad$ $-\pi <\varphi \leqslant \pi$).

Такие ограничения на значения полярных координат ставятся для того, чтобы соответствие между точками плоскости, отличными от полюса, и парами полярных координат $(\rho ,\varphi )$ получилось взаимно однозначным.

Главное значение полярного угла — значение полярного угла $\varphi$, при котором получается взаимно-однозначное соответствие между точками плоскости, отличными от полюса, и парами полярных координат. Как правило, это значения $0\leqslant \varphi <2\pi$ (иногда используются значения $-\pi <\varphi \leqslant \pi$).

Замечание. Часто требуется в ущерб однозначности поддерживать непрерывное изменение полярных координат точек (например, у уравнениях, описывающих кривые на плоскости). Тогда отказываются от приведённых ограничений для $\rho$ и $\varphi$. Закон изменения значений полярных координат $\rho$ и $\varphi$ выясняется в каждом конкретном случае. Например:

• при вращении некоторой точки по окружности в обе стороны (когда $\rho ={\text{const}}$) естественно считать, что полярный угол этой точки может принимать значения, большие $2\pi$ или меньшие нуля;
• при движении точки по прямой, проходящей через полюс (когда $\varphi ={\text{const}}$), естественно считать, что при переходе через полюс полярный радиус точки меняет знак.

Обобщённая полярная система координат — система координат на плоскости, определяющаяся двумя обобщёнными полярными координатами $r$ и $\psi$, которые связаны с декартовыми прямоугольными координатами $x$ и $y$ следующими выражениями:

$x=ar\cos \psi ,\quad$ $y=br\sin \psi ,$

где $\quad 0\leqslant r<+\infty ,\quad$ $0\leqslant \psi <2\pi ,\quad$ $a,b>0,\quad$ $a\neq b$. Координатные линии суть эллипсы при $r={\text{const}}$ и лучи при $\psi ={\text{const}}$.

Полярную систему координат в трёхмерном пространстве представляют цилиндрическая система координат и сферическая система координат.

Связь декартовых координат с полярными

Иногда приходится одновременно использовать и полярную и декартову системы координат. в такой ситуации появляются две задачи: по полярным координата некоторой точки определить её декартовы координаты, и наоборот. Решим эти две задачи в частном случае, когда полярная и декартова системы координат связаны определённым образом.

Если на плоскости задана некоторая полярная система координат, то тем самым задана и следующая строго определённая декартова система координат, и наоборот.

Декартова система координат, определённая данной полярной — система координат, определённая следующим образом:

• масштаб декартовой системы равен масштабу полярной;
• начало декартовой системы $O$ совпадает с началом полярной $O$;
• положительная полуось абсцисс $Ox$ декартовой системы совпадает с полярной осью $Ox$;
• ориентация декартовой системы совпадает с ориентацией полярной;
• ось ординат $Oy$ декартовой системы совпадает с её осью абсцисс $Ox$, повёрнутой на угол $\varphi ={\frac {\pi }{2}}$ в положительном направлении.

Полярная система координат, определённая данной декартовой — система координат, определённая следующим образом:

• масштаб полярной системы равен масштабу декартовой;
• начало полярной системы $O$ совпадает с началом декартовой $O$;
• полярная ось $Ox$ совпадает с положительной полуосью абсцисс $Ox$ декартовой системы;
• ориентация полярной системы совпадает с ориентацией декартовой;
• полярная ось $Ox$, повёрнутая на угол $\varphi ={\frac {\pi }{2}}$ в положительном направлении, совпадает с положительной полуосью ординат $Oy$ декартовой системы.

Если для данной декартовой системы координат построить определённую ею полярную, а потом для этой полярной системы координат построить определённую ею декартову, то получится исходная декартова система координат. И наоборот.

Теорема 1. Каждой декартовой системы координат соответствует строго определённая полярная, и наоборот.

Полярные и декартовы координаты

Теорема 2. Формулы, выражающие декартовы координаты через полярные, имеют следующий вид:

$x=\rho \cos \varphi ,\quad$ $y=\rho \sin \varphi .$

Две декартовы координаты $x$ и $y$ могут быть переведены в полярную координату $r$:

$r^{2}=y^{2}+x^{2}$ (по теореме Пифагора).

Для определения угловой координаты $\varphi$ следует принять во внимание два следующих соображения:

• Для ${r\equiv 0}$, $\varphi$ может быть произвольным действительным числом.
• Для $r\neq 0$, чтобы получить уникальное значение $\varphi$, следует ограничиться интервалом в $2\pi$. Обычно выбирают интервал $[0,\;2\pi )$ или $(-\pi ,\;\pi ]$.

Для вычисления $\varphi$ в интервале $[0,\;2\pi )$, можно воспользоваться такими уравнениями ($\mathrm {arctg}$ обозначает обратную функцию к тангенсу):

$\varphi ={\begin{cases}\operatorname {arctg} ({\frac {y}{x}}),&x>0,y\geq 0\\\operatorname {arctg} ({\frac {y}{x}})+2\pi ,&x>0,y<0\\\operatorname {arctg} ({\frac {y}{x}})+\pi ,&x<0\\{\frac {\pi }{2}},&x=0,y>0\\{\frac {3\pi }{2}},&x=0,y<0\\-&x=0,y=0\end{cases}}$.

Для вычисления $\varphi$ в интервале $(-\pi ,\;\pi ]$, можно воспользоваться такими уравнениями:

$\varphi ={\begin{cases}\operatorname {arctg} ({\frac {y}{x}}),&x>0\\\operatorname {arctg} ({\frac {y}{x}})+\pi ,&x<0,y\geq 0\\\operatorname {arctg} ({\frac {y}{x}})-\pi ,&x<0,y<0\\{\frac {\pi }{2}},&x=0,y>0\\-{\frac {\pi }{2}},&x=0,y<0\\-&x=0,y=0\end{cases}}$.

Учитывая, что для вычисления полярного угла недостаточно знать отношение $y$ к $x$, а ещё нужны знаки одного из этих чисел, многие из современных языков программирования имеют среди своих функций помимо функции atan, определяющей арктангенс числа, ещё и дополнительную функцию atan2, которая имеет отдельные аргументы для числителя и знаменателя. В языках программирования, поддерживающих необязательные аргументы (например, в Common Lisp), функция atan может получать значение координаты $x$. Однако можно заметить, что независимо от знаков декартовых координат, частные производные угла по ним вычисляются довольно просто, благодаря чему получаем удобные матрицы Якоби:

$J=\det {\frac {\partial (x,\;y)}{\partial (r,\;\varphi )}}={\begin{vmatrix}{\dfrac {\partial x}{\partial r}}&{\dfrac {\partial x}{\partial \varphi }}\\{\dfrac {\partial y}{\partial r}}&{\dfrac {\partial y}{\partial \varphi }}\end{vmatrix}}={\begin{vmatrix}\cos(\varphi )&-r\sin(\varphi )\\\sin(\varphi )&r\cos(\varphi )\end{vmatrix}}.$

$J^{-1}=\det {\frac {\partial (r,\;\varphi )}{\partial (x,\;y)}}={\begin{vmatrix}{\dfrac {\partial r}{\partial x}}&{\dfrac {\partial r}{\partial y}}\\{\dfrac {\partial \varphi }{\partial x}}&{\dfrac {\partial \varphi }{\partial y}}\end{vmatrix}}={\begin{vmatrix}\cos(\varphi )&\sin(\varphi )\\-{\dfrac {1}{r}}\sin(\varphi )&{\dfrac {1}{r}}\cos(\varphi )\end{vmatrix}}.$

Уравнение кривых в полярных координатах

Благодаря радиальной природе полярной системы координат, некоторые кривые могут быть достаточно просто описаны полярным уравнением, тогда как уравнение в прямоугольной системе координат было бы намного сложнее. Среди самых известных кривых: полярная роза, архимедова спираль, Лемниската, улитка Паскаля и кардиоида.

Окружность

Окружность, заданная уравнением $\scriptstyle {r(\varphi )=1}$

Общее уравнение окружности с центром в ($r_{0},\;\theta$) и радиусом $a$ имеет вид:

$r^{2}-2rr_{0}\cos(\varphi -\theta )+r_{0}^{2}=a^{2}.$

Это уравнение может быть упрощено для частных случаев, например

$r(\varphi )=a$

является уравнением, определяющим окружность с центром в полюсе и радиусом $a$.

Прямая

Радиальные прямые (те, которые проходят через полюс) определяются уравнением

$\varphi =\theta$,

где $\theta$ — угол, на который прямая отклоняется от полярной оси, то есть, $\theta =\mathrm {arctg} \,m$, где $m$ — наклон прямой в прямоугольной системе координат. Нерадиальная прямая, перпендикулярно пересекает радиальную прямую $\varphi =\theta$ в точке $(r_{0},\;\theta )$ определяется уравнением

$r(\varphi )=r_{0}\sec(\varphi -\theta ).$

Полярная роза

Полярная роза задана уравнением $\scriptstyle {r(\varphi )=2\sin 4\varphi }$

Полярная роза — известная математическая кривая, похожая на цветок с лепестками. Она может быть определена простым уравнением в полярных координатах:

$r(\varphi )=a\cos(k\varphi +\theta _{0})$

для произвольной постоянной $\theta _{0}$ (включая 0). Если $k$ — целое число, то это уравнение будет определять розу с $k$ лепестками для нечётных $k$, либо с $2k$ лепестками для чётных $k$. Если $k$ — рациональное, но не целое, график, заданный уравнением, образует фигуру, подобную розе, но лепестки будут перекрываться. Если $k$ — иррациональное, то роза состоит из бесконечного множества частично накладывающихся друг на друга лепестков. Розы с 2, 6, 10, 14 и т. д. лепестками этим уравнением определить невозможно. Переменная $a$ определяет длину лепестков.

Если считать, что радиус не может быть отрицательным, то при любом натуральном $k$ мы будем иметь $k$-лепестковую розу. Таким образом, уравнение $r(\varphi )=\cos(2\varphi )$ будет определять розу с двумя лепестками. С геометрической точки зрения радиус — это расстояние от полюса до точки и он не может быть отрицательным.

Спираль Архимеда

Одна из ветвей спирали Архимеда, задаваемая уравнением $\scriptstyle {r(\varphi )=\varphi }$ для $\scriptstyle {0<\theta <6\pi }$

Архимедова спираль названа в честь её изобретателя, древнегреческого математика Архимеда. Эту спираль можно определить с помощью простого полярного уравнения:

$r(\varphi )=a+b\varphi .$

Изменения параметра $a$ приводят к повороту спирали, а параметра $b$ — расстояния между витками, которое является константой для конкретной спирали. Спираль Архимеда имеет две ветви, одну для $\varphi >0$ а другую для $\varphi <0$. Две ветви плавно соединяются в полюсе. Зеркальное отображение одной ветви относительно прямой, проходящей через угол 90°/270°, даст другую ветвь. Эта кривая интересна тем, что была описана в математической литературе одной из первых, после конического сечения, и лучше других определяется именно полярным уравнением.

Конические сечения

Эллипс

Коническое сечение, один из фокусов которого находится в полюсе, а другой где-то на полярной оси (так, что большая полуось лежит вдоль полярной оси) задаётся уравнением:

$r={\frac {\ell }{1-e\cos \varphi }}$,

где $e$ — эксцентриситет, а $\ell$ — фокальный параметр. Если $e>1$, это уравнение определяет гиперболу; если $e=1$, то параболу; если $e<1$, то эллипс. Отдельным случаем является $e=0$, определяющее окружность с радиусом $\ell$.

Комплексные числа

Пример комплексного числа $\scriptstyle {z}$, нанесённого на комплексную плоскость

Пример комплексного числа, нанесённого на график, с использованием формулы Эйлера

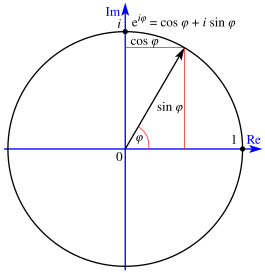
Каждое комплексное число может быть представлено точкой на комплексной плоскости, и, соответственно, эта точка может определяться в декартовых координатах (прямоугольная или декартова форма), либо в полярных координатах (полярная форма). Комплексное число $z$ может быть записано в прямоугольной форме так:

$z=x+iy$,

где $i$ — мнимая единица, или в полярной (см. формулы преобразования между системами координат выше):

$z=r\cdot (\cos \varphi +i\sin \varphi )$

и отсюда:

$z=re^{i\varphi }$,

где $e$ — число Эйлера. Благодаря формуле Эйлера, оба представления эквивалентны (В этой формуле, подобно остальным формулам, содержащим возведения в степень углов, угол $\varphi$ задан в радианах)

Для перехода между прямоугольным и полярным представлением комплексных чисел, могут использоваться указанные выше формулы преобразования между системами координат.

Операции умножения, деления и возведения в степень с комплексными числами, как правило, проще проводить в полярной форме. Согласно правилам возведения в степень:

• Умножение:

$r_{0}e^{i\varphi _{0}}\cdot r_{1}e^{i\varphi _{1}}=r_{0}r_{1}e^{i(\varphi _{0}+\varphi _{1})}.$

• Деление:

${\frac {r_{0}e^{i\varphi _{0}}}{r_{1}e^{i\varphi _{1}}}}={\frac {r_{0}}{r_{1}}}e^{i(\varphi _{0}-\varphi _{1})}.$

• Возведение в степень (формула Муавра):

$(re^{i\varphi })^{n}=r^{n}e^{in\varphi }.$

В математическом анализе

Операции математического анализа тоже можно сформулировать, используя полярные координаты.

Дифференциальное исчисление

Справедливы следующие формулы:

$r{\frac {\partial }{\partial r}}=x{\frac {\partial }{\partial x}}+y{\frac {\partial }{\partial y}},$

${\frac {\partial }{\partial \varphi }}=-y{\frac {\partial }{\partial x}}+x{\frac {\partial }{\partial y}}.$

Чтобы найти тангенс угла наклона касательной к любой данной точке полярной кривой $r(\varphi )$ в декартовых координатах, выразим их через систему уравнений в параметрическом виде:

$x=r(\varphi )\cos \varphi ,$

$y=r(\varphi )\sin \varphi .$

Дифференцируя оба уравнения по $\varphi$ получим:

${\frac {dx}{d\varphi }}=r'(\varphi )\cos \varphi -r(\varphi )\sin \varphi ,$

${\frac {dy}{d\varphi }}=r'(\varphi )\sin \varphi +r(\varphi )\cos \varphi .$

Разделив эти уравнения (второе на первое), получим искомый тангенс угла наклона касательной в декартовой системе координат в точке $(r,\;r(\varphi ))$:

${\frac {dy}{dx}}={\frac {r'(\varphi )\sin \varphi +r(\varphi )\cos \varphi }{r'(\varphi )\cos \varphi -r(\varphi )\sin \varphi }}.$

Интегральное исчисление

Область $\scriptstyle {R}$, которая образована полярной кривой $\scriptstyle {r(\varphi )}$ и лучами $\scriptstyle {\varphi =a}$ и $\scriptstyle {\varphi =b}$

Пусть $R$ — область, которую образуют полярная кривая $r(\varphi )$ и лучи $\varphi =a$ и $\varphi =b$, где $0<b-a<2\pi$. Тогда площадь этой области находится определённым интегралом:

${\frac {1}{2}}\int \limits _{a}^{b}[r(\varphi )]^{2}\,d\varphi .$

Область $\scriptstyle {R}$ образована из $n$ секторов (тут $\scriptstyle {n=5}$)

Такой результат можно получить следующим образом. Сначала разобьём интервал $[a,\;b]$ на произвольное число подынтервалов $n$. Таким образом, длина такого подынтервала $\Delta \varphi$ равна $b-a$ (полная длина интервала), разделённая на $n$ (число подынтервалов). Пусть для каждого подынтервала $i=1,\;2,\;\ldots ,\;n$ $\varphi _{i}$ — средняя точка. Построим секторы с центром в полюсе, радиусами $r(\varphi _{i})$, центральными углами $\Delta \varphi$ и длиной дуги $r(\varphi _{i})\Delta \varphi$. Поэтому площадь каждого такого сектора будет ${\frac {1}{2}}r(\varphi _{i})^{2}\Delta \varphi$. Отсюда, полная площадь всех секторов:

$\sum _{i=1}^{n}{\frac {1}{2}}r(\varphi _{i})^{2}\,\Delta \varphi .$

Если число подынтервалов $n$ увеличивать, то погрешность такого приближенного выражения будет уменьшаться. Положив $n\to \infty$, полученная сумма станет интегральной. Предел этой суммы при $\Delta \varphi \to 0$ определяет вышеописанный интеграл:

$\lim _{\Delta \varphi \to 0}\sum _{i=1}^{\infty }{\frac {1}{2}}r(\varphi _{i})^{2}\,\Delta \varphi ={\frac {1}{2}}\int \limits _{a}^{b}[r(\varphi )]^{2}\,d\varphi .$

Обобщение

Используя декартовы координаты, площадь бесконечно малого элемента может быть вычислена как $dA=dx\,dy$. При переходе к другой системе координат в многократных интегралах необходимо использовать определитель Якоби:

$J=\det {\frac {\partial (x,\;y)}{\partial (r,\;\varphi )}}={\begin{vmatrix}{\dfrac {\partial x}{\partial r}}&{\dfrac {\partial x}{\partial \varphi }}\\{\dfrac {\partial y}{\partial r}}&{\dfrac {\partial y}{\partial \varphi }}\end{vmatrix}}.$

Для полярной системы координат, определитель матрицы Якоби равен $r$:

$J={\begin{vmatrix}\cos \varphi &-r\sin \varphi \\\sin \varphi &r\cos \varphi \end{vmatrix}}=r\cos ^{2}\varphi +r\sin ^{2}\varphi =r.$

Следовательно, площадь элемента в полярных координатах можно записать так:

$dA=J\,dr\,d\varphi =r\,dr\,d\varphi .$

Теперь, функция, записанная в полярных координатах, может быть интегрирована следующим образом:

$\iint \limits _{R}f(r,\;\varphi )\,dA=\int \limits _{a}^{b}\int \limits _{0}^{r(\varphi )}f(r,\;\varphi )\,r\,dr\,d\varphi .$

Здесь область $R$, как и в предыдущем разделе, такая, которую образуют полярная кривая $r(\varphi )$ и лучи $\varphi =a$ и $\varphi =b$.

Формула для вычисления площади, описанная в предыдущем разделе, получена в случае $f=1$. Интересным результатом применения формулы для многократных интегралов является Интеграл Эйлера — Пуассона:

$\int \limits _{-\infty }^{\infty }e^{-x^{2}}\,dx={\sqrt {\pi }}.$

Векторный анализ

Для полярных координат можно применить элементы векторного анализа. Любое векторное поле $\mathbf {F}$ на двумерном пространстве (плоскости) можно записать в полярной системе координат, используя единичные векторы:

$\mathbf {e} _{r}=(\cos \varphi ,\;\sin \varphi )$

в направлении $\mathbf {r}$, и

$\mathbf {e} _{\varphi }=(-\sin \varphi ,\;\cos \varphi );$

$\mathbf {F} =F_{r}\mathbf {e} _{r}+F_{\varphi }\mathbf {e} _{\varphi }.$

Связь между декартовыми компонентами поля $F_{x}$ и $F_{y}$ и его компонентами в полярной системе координат задаётся уравнениями:

$F_{x}=F_{r}\cos \varphi -F_{\varphi }\sin \varphi ;$

$F_{y}=F_{r}\sin \varphi +F_{\varphi }\cos \varphi .$

Соответствующим образом в полярной системе координат определяются операторы векторного анализа. Например, градиент скалярного поля $\Phi (r,\;\varphi )$ записывается:

$\mathrm {grad} \,\Phi ={\frac {\partial \Phi }{\partial r}}\mathbf {e} _{r}+{\frac {1}{r}}{\frac {\partial \Phi }{\partial \varphi }}\mathbf {e} _{\varphi }.$

Всё это работает за исключением одной особой точки — полюса, для которой $\varphi$ не определено, и векторный базис, описанный выше, построить таким образом в данной точке нельзя. Это надо иметь в виду, хотя на практике векторные поля, исследуемые с помощью полярных координат, часто или сами имеют особенность в этой точке, или равны в ней нулю, что несколько облегчает дело. Кроме того, использование полярных координат никак не затрудняет выражение произвольного векторного поля сколь угодно близко к этой точке.

Трёхмерное расширение

Полярная система координат распространяется в третье измерение двумя системами: цилиндрической и сферической, обе содержат двумерную полярную систему координат как подмножество. По сути, цилиндрическая система расширяет полярную добавлением ещё одной координаты расстояния, а сферическая — ещё одной угловой координаты.

Цилиндрические координаты

Точка $\scriptstyle {P}$ начертана в цилиндрической системе координат

Основная статья: Цилиндрическая система координат

Цилиндрическая система координат, грубо говоря, расширяет плоскую полярную систему добавлением третьей линейной координаты, называемой «высотой» и равной высоте точки над нулевой плоскостью подобно тому, как декартова система расширяется на случай трёх измерений. Третья координата обычно обозначается как $z$, образуя тройку координат $(\rho ,\;\varphi ,\;z)$.

Тройку цилиндрических координат можно перевести в декартову систему следующими преобразованиями:

${\begin{cases}x=\rho \cos \varphi ;\\y=\rho \sin \varphi ;\\z=z.\end{cases}}$

Сферические координаты

Точка начертана в сферической системе координат

Основная статья: Сферическая система координат

Также полярные координаты можно расширить на случай трёх измерений путём добавления угловой координаты $\theta$, равным углу поворота от вертикальной оси $z$ (называется зенитом или широтой, значения находятся в интервале от 0 до 180°). То есть, сферические координаты, это тройка $(r,\;\varphi ,\;\theta )$, где $r$ — расстояние от центра координат, $\varphi$ — угол от оси $x$ (как и в плоских полярных координатах), $\theta$ — широта. Сферическая система координат подобна географической системе координат для определения места на поверхности Земли, где начало координат совпадает с центром Земли, широта $\delta$ является дополнением $\theta$ и равна $\delta =90^{\circ }-\theta$, а долгота $l$ вычисляется по формуле $l=\varphi -180^{\circ }$.

Тройку сферических координат можно перевести в декартову систему следующими преобразованиями:

${\begin{cases}x=r\sin \theta \cos \varphi ;\\y=r\sin \theta \sin \varphi ;\\z=r\cos \theta .\end{cases}}$

Обобщение на n измерений

Полярную систему координат можно расширить на случай $n$-мерного пространства. Пусть $x_{i}\in \mathbb {R}$, $i=1,\;\ldots ,\;n$ — координатные векторы $n$-мерной прямоугольной системе координат. Необходимые координаты в $n$-мерный полярной системе можно вводить как угол отклонения вектора $x\in \mathbb {R} ^{n}$ от координатной оси $x_{i+2}$.

Для перевода обобщённых $n$-мерных полярных координат в декартовы можно воспользоваться следующими формулами:

${\begin{array}{lcr}x_{1}&=&r\cos \varphi \sin \vartheta _{1}\sin \vartheta _{2}\ldots \sin \vartheta _{n-3}\sin \vartheta _{n-2};\\x_{2}&=&r\sin \varphi \sin \vartheta _{1}\sin \vartheta _{2}\ldots \sin \vartheta _{n-3}\sin \vartheta _{n-2};\\x_{3}&=&r\cos \vartheta _{1}\sin \vartheta _{2}\ldots \sin \vartheta _{n-3}\sin \vartheta _{n-2};\\x_{4}&=&r\cos \vartheta _{2}\ldots \sin \vartheta _{n-3}\sin \vartheta _{n-2};\\\ldots &\ldots &\ldots \qquad \qquad \qquad \\x_{n-1}&=&r\cos \vartheta _{n-3}\sin \vartheta _{n-2};\\x_{n}&=&r\cos \vartheta _{n-2}.\end{array}}$

Как можно показать, случай $n=2$ соответствует обычной полярной системе координат на плоскости, а $n=3$ — обычной сферической системе координат.

Якобиан преобразования полярных координат в декартовы даётся формулой:

$\det {\frac {\partial (x_{1},\;\ldots ,\;x_{n})}{\partial (r,\;\varphi ,\;\vartheta _{1},\;\ldots ,\;\vartheta _{n-2})}}=r^{n-1}\sin \vartheta _{1}(\sin \vartheta _{2})^{2}\ldots (\sin \vartheta _{n-2})^{n-2}$,

где $n$-мерный элемент объёма имеет вид:

$dV=r^{n-1}\sin \vartheta _{1}(\sin \vartheta _{2})^{2}\ldots (\sin \vartheta _{n-2})^{n-2}\,dr\,d\varphi \,d\vartheta _{1}\ldots d\vartheta _{n-2}=$

$=r^{n-1}\,dr\,d\varphi \prod \limits _{j=1}^{n-2}(\sin \vartheta _{j})^{j}\,d\vartheta _{j}.$

Применение

Полярная система координат двумерная и поэтому может применяться только в тех случаях, когда местонахождение точки определяется на плоскости, или для случая однородности свойств системы в третьем измерении, например, при рассмотрении течения в круглой трубе. Лучшим контекстом применения полярных координат являются случаи, тесно связанные с направлением и расстоянием от некоторого центра. Например, в приведённых выше примерах видно, что простых уравнений в полярных координатах достаточно для определения таких кривых как спираль Архимеда, уравнения которых в прямоугольной системе координат гораздо сложнее. Кроме того, многие физические системы — такие, которые содержат тела, движущиеся вокруг центра, либо явления, распространяющиеся из некоторого центра — гораздо проще моделировать в полярных координатах. Поводом создания полярной системы координат было исследование орбитального и движения по кругу, впоследствии оказалось, что она крайне удобна иногда и для исследования некругового движения (см. Кеплерова задача).

Позиционирование и навигация

Полярную систему координат часто применяют в навигации, поскольку пункт назначения можно задать как расстояние и направление движения от отправной точки. Например, в авиации, для навигации применяют несколько изменённую версию полярных координат. В этой системе, обычно используемой для навигации, луч 0° называют направлением 360, а углы отсчитываются в направлении по часовой стрелке. Направление 360 соответствует магнитному северу, а направления 90, 180, и 270 соответствуют магнитным востоку, югу и западу. Так, самолёт, летящий 5 морских миль на восток можно описать как самолёт, летящий 5 единиц в направлении 90 (центр управления полётами назовёт его найн-зиро).

Применение в физике

Cечение комптоновского рассеяния от угла рассеяния (для разной энергии фотона)

Системы с радиальной симметрией очень хорошо подходят для описания в радиальных координатах, где полюс системы координат совпадает с центром симметрии. В качестве примера можно привести уравнение тока грунтовых вод в случае радиально симметричных колодцев. Системы с центральными силами также подходят для моделирования в полярных координатах. К таким системам относятся гравитационные поля, подчиняющиеся закону обратно-квадратичной зависимости, и вообще центральные силы. Также существенное удобство полярные координаты предоставляют при работе с системами, имеющими точечные (или приближенно точечные) источники энергии, такие как радиоантенны — при исследовании их излучения на сравнительно больших расстояниях от антенны, распространение звука или света — в особенности (но не обязательно) сферически- или цилиндрически-симметричное. В определённых задачах, в том числе из числа упомянутых выше, использование сферических или цилиндрических координат (являющихся для этих задач естественными) по сути сводится к использованию просто двумерных полярных координат.

Полярные координаты как для вычислений, так и для наглядного изображения их результатов, бывают достаточно полезны не только в случаях, когда симметрия задачи близка в целом к осевой или сферической, но и в случаях, когда симметрия явно далека от таковой, например, для вычисления поля диполя. В этом случае применение полярных координат имеет мотивировку в малом размере источника поля (заряды диполя расположены очень близко друг к другу), к тому же поле каждого такого заряда просто выражается в полярных координатах, особенно если поместить полюс в один из этих зарядов (поле второго будет отличаться, кроме знака, лишь на малую поправку).

В квантовой механике и химии полярные координаты (наряду со сферическими для более сложных случаев) используются для изображения угловой зависимости волновой функции электрона в атоме, в том числе в целях качественного анализа и наглядности при преподавании.

Применение в прикладных целях, диаграммы направленности

Диаграмма направленности (азимутальная) типичной направленной антенны

Фронт мощности звуковой волны промышленного громкоговорителя показан в сферических координатах при шести частотах

В разных прикладных областях, полярные координаты применяются как способами, близкими к применяемым в соответствующих областям фундаментальной физики, так и самостоятельным образом.

Трёхмерное моделирование звука динамиков может использоваться для прогнозирования их эффективности. Необходимо сделать несколько диаграмм в полярных координатах для широкого диапазона частот, поскольку фронт существенно меняется в зависимости от частоты звука. Полярные диаграммы помогают увидеть, что многие громкоговорители с понижением частоты звука теряют направленность. В случае излучателя, имеющего строгую осевую симметрию или слабо от неё отклоняющегося, достаточно использовать не сферические, а обычные (двумерные) полярные координаты, так как во всех плоскостях, проходящих через ось симметрии, зависимость будет одинаковой или почти одинаковой. Если такой симметрии нет, то какое-то представление о звуковом потоке в разных направлениях может дать пара (для каждой частоты) полярных диаграмм в перпендикулярных плоскостях, для эллиптического или прямоугольного излучателя — связанного с его главными осями.

В полярных координатах также принято представлять характеристику направленности микрофонов, определяемую отношением чувствительности при падении звуковой волны под углом относительно акустической оси микрофона к его осевой чувствительности.

В принципе, полярные диаграммы могут использоваться для представления практически любых зависимостей. Но на практике обычно этот вид представления выбирается в случаях, когда речь идет от зависимости от реального геометрического направления (см. например Роза ветров, Диаграмма рассеяния, зависимость отраженного светового потока от угла в фотометрии, диаграмма направленности антенн, светодиодов и других светоизлучателей, фотодатчиков, акустических систем итп). Также довольно нередко можно встретиться с применением полярных координат в случаях, когда одна из переменных имеет циклический характер (в полярных координатах её довольно естественно представлять углом).

Могут применяться и областях, не связанных прямо с физикой (хотя иногда можно проследить более или менее прямую аналогию в этом плане), например, можно использовать полярные диаграммы, аналогичные розе ветров, например, для изучения направлений миграций животных. Такое использование достаточно удобно и наглядно.

Источники

• Александров П. С. Лекции по аналитической геометрии, пополненные необходимыми сведениями из алгебры с приложением собрания задач, снабжённых решениями, составленного А. С, Пархоменко. 2-е изд. М.: «Наука», 1968. 912 с., ил.
• Выгодский М. Я. Справочник по высшей математике. Изд-е 12-е, стереотип. М.: «Наука», 1977. 871 с., ил.
• Гельфанд И. М., Глаголева Е. Г., Кириллов А. А. Метод координат. 5-е изд., стереот. М.: «Наука», 1973. 87 с., ил. (Серия «Математика. Библиотечка физико-математической школы» под ред. И. М. Гельфанда.)
• Ефимов Н. В. Краткий курс аналитической геометрии: Учебное пособие. 13-е изд., стереот. М.: Физматлит, 2005. 238 с. ISBN 5-9221-0252-4.
• Ильин В. А., Позняк Э. Г. Аналитическая геометрия: Учебник для университетов. 4-е изд., доп. М.: «Наука», 1988. 223 с. (Курс высшей математики и математической физики. Выпуск 5 / Под ред. А. Н. Тихонова, В. А. Ильина, А. Г. Свешникова).
• Полюс // Математический энциклопедический словарь / Гл. ред. Ю. В. Прохоров; Ред. Кол.: С. И. Адян, Н. С. Бахвалов, В. И. Битюцков, А. П. Ершов, Л. Д. Кудрявцев, А. Л. Онищик, А. П. Юшкевич. М.: «Советская энциклопедия», 1988. 847 с., ил. С. 474.
• Полярная система координат // Воднев В. Т., Наумович А. Ф., Наумович Н. Ф. Математический словарь высшей школы: Общая часть / Под. ред. Ю. С. Богданова. Минск: «Высшая школа», 1984. 527 с., ил. С. 320—321.
• Полярные координаты // Большая советская энциклопедия. (В 30 томах) Гл. ред. А. М. Прохоров. Изд. 3-е. М.: «Советская энциклопедия», 1975. Т. 20. Плата — Проб. 1975. 608 с. с илл., 17 л. илл., 4 л. карт. С. 338. Полярные координаты // БСЭ 3-е издание. Основной вариант Архивная копия от 7 апреля 2023 на Wayback Machine
• Полярные координаты // Математический энциклопедический словарь / Гл. ред. Ю. В. Прохоров; Ред. Кол.: С. И. Адян, Н. С. Бахвалов, В. И. Битюцков, А. П. Ершов, Л. Д. Кудрявцев, А. Л. Онищик, А. П. Юшкевич. М.: «Советская энциклопедия», 1988. 847 с., ил. С. 475.
• Соколов Д. Д. Полярные координаты // Математическая энциклопедия: Гл. ред. И. М. Виноградов, т. 4 Ок—Сло. М.: «Советская Энциклопедия», 1984. 1216 стб., ил. Стб. 480—481.

Ссылки

• Программы для рисования графиков в каталоге ссылок Curlie (dmoz)