Przejdź do zawartości

Moc testu

Z Wikipedii, wolnej encyklopedii
Przy niskiej mocy rozkłady prawdopodobieństwa dla statystyki testowej w hipotezie zerowej i alternatywnej znacząco się pokrywają, więc test nie rozróżnia ich rzetelnie
Rozkłady prawdopodobieństwa dla statystyki testowej w hipotezie zerowej i alternatywnej, w teście t dla dwóch grup niezależnych, przy N=60, d=0,2 co oznacza poziom mocy statystycznej ok. 12%
Przy mocy ok. 70% rozkłady prawdopodobieństwa dla statystyki testowej w hipotezie zerowej i alternatywnej w znacznej części nie pokrywają się
Rozkłady prawdopodobieństwa dla statystyki testowej w hipotezie zerowej i alternatywnej, w teście t dla dwóch grup niezależnych, przy N=100, d=0,5 co oznacza poziom mocy statystycznej ok. 70%
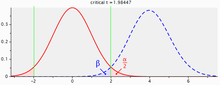
Przy bardzo wysokiej mocy rozkłady prawdopodobieństwa statystyki testowej w hipotezie zerowej i alternatywnej pokrywają się w bardzo małym stopniu, i test z wysokim prawdopodobieństwem dobrze je rozróżni
Rozkłady prawdopodobieństwa dla statystyki testowej w hipotezie zerowej i alternatywnej, w teście t dla dwóch grup niezależnych, przy N=100, d=0,8 co oznacza poziom mocy statystycznej ok. 98%
Wizualny nomogram pozwalający oszacować moc testu dla określonej wielkości efektu.
Nomogram pozwalający oszacować moc statystyczną lub wielkość próby przy określonej wielkości efektu, dla prostych testów jak test t-Studenta.
Nawet przy mocy 80% i badaniu prawdziwego zjawiska, można się spodziewać, że tylko w 51,2% przypadków trzy na trzy replikacje badania przyniosą istotny wynik.
Nawet przy mocy 80% i badaniu prawdziwego zjawiska, można się spodziewać, że tylko w 51,2% przypadków trzy na trzy replikacje badania przyniosą istotny wynik.

Moc testu (moc statystyczna) to prawdopodobieństwo uniknięcia błędu drugiego rodzaju – przyjęcia hipotezy zerowej, gdy w rzeczywistości jest ona fałszywa. Im większe jest to prawdopodobieństwo, tym lepszy jest dany test jako narzędzie do różnicowania między hipotezą prawdziwą i fałszywą. Moc można wyrazić jako dopełnienie prawdopodobieństwa popełnienia błędu drugiego rodzaju (β), czyli 1-β. Pojęcie to wywodzi się z podejścia częstościowego w metodologii weryfikacji hipotez statystycznych[1].

Moc zależy bezpośrednio i przede wszystkim od poniższych czynników:

Testy różnią się ponadto mocą pomiędzy sobą, w zależności od tego na ile są stratne informacyjne, oraz w jakim stopniu leżący u ich podłoża model statystyczny jest w konkretnej sytuacji dostosowany do problemu badawczego i charakteru danych[1][2].

Wysoka moc statystyczna w projektowanych badaniach zwiększa precyzję i wiarygodność oszacowań. Realizowanie badań o niskiej mocy może być marnotrawstwem zasobów, ponieważ już na wstępie nie mają szans uzyskać konkluzywnych rezultatów. Niska moc w połączeniu z efektem szuflady zaburza proporcje pomiędzy błędami I i II rodzaju oraz prawidłowymi rozpoznaniami w publikacjach, i zniekształca naukowy obraz rzeczywistości. Statystyk Jacob Cohen zalecił badaczom i wydawcom publikacji naukowych dążenie do przyjęcia konwencjonalnego poziomu mocy co najmniej 0,8 – analogicznie do używania konwencjonalnego poziomu istotności α=0,05[1][3][4][5].

Zastrzeżenia interpretacyjne

[edytuj | edytuj kod]

Moc odnosi się zawsze do konkretnego testu. Nawet jeśli ogólna próba w badaniu liczy znacznie więcej uczestników, pojedynczy test ma tylko taką moc, na jaką pozwala wielkość konkretnego efektu i liczebność określonych porównywanych podgrup. W przypadku testów interakcji, których wielkość jest dodatkowo ograniczona przez efekty główne, Gelman uznaje za realistyczną możliwość aż 16-krotnie niższej mocy w porównaniu do testu ogólnego[6].

Moc statystyczna jest w praktyce zmienną losową, która jest funkcją wielu nieznanych parametrów populacji i próby. Można ją oszacować, stosując odpowiednie założenia dotyczące tych zmiennych lub ich szacunki, lecz jak podkreślają m.in. Wagenmakers i in., jest to zawsze tylko zawodne oszacowanie jej wartości oczekiwanej lub rozkładu[7][8]. Interpretacja oszacowań mocy zależy zatem od wiarygodności założeń badaczy, przede wszystkim dotyczących wielkości efektu w populacji i trafności modelu. Gelman i Carlin zaproponowali, aby rozważanie mocy zastąpić dokładniejszymi pytaniami, dotyczącymi tego, na jaką precyzję i wiarygodność oszacowań pozwala badanie o danym charakterze. Ci i inni autorzy zademonstrowali przy pomocy symulacji, że niska moc zwiększa ryzyko, że wyniki „istotne statystycznie” będą miały skrajnie błędne wartości[5][9].

Określenie wielkości efektu w analizie mocy

[edytuj | edytuj kod]

Historycznie popularnym sposobem przyjęcia wielkości efektu używanego do oszacowania mocy było odwołanie się do istniejących badań. Lakens sugeruje, by zamiast tego naukowcy wyznaczali po prostu najmniejszy poziom efektu, jaki uznaliby za interesujący[10][11][12]. Hoenig i Heisey przestrzegają szczególnie przed wyznaczaniem mocy testu na podstawie obserwowanej w próbie wielkości efektu, zaznaczając, że tworzy to błędne koło i prowadzi do niewiarygodnych wniosków[13].

Metody zwiększania mocy badań

[edytuj | edytuj kod]

Zabiegi jakie umożliwiają naukowcom zwiększenie mocy statystycznej badań to np. [1]:

  • zwiększenie próby badawczej – szczególnie przez określenie z wyprzedzeniem oczekiwanej wielkości efektu, np. na podstawie badań innych autorów, lub własnych badań pilotażowych, i wykonanie analizy mocy a priori w celu ustalenia wielkości próby zapewniającej testom pożądany poziom oczekiwanej mocy[14]; rekomenduje się przy tym, aby traktować oszacowania pochodzące z małych pilotaży konserwatywnie, i jedynie orientacyjnie[15] – względnie najwiarygodniejsze przybliżenia wielkości efektu zapewniają metaanalizy[16],
  • redukcja losowej zmienności obserwowanej w próbach, np. przez wykorzystanie statystyk odpornościowych[17], oraz metod pomiaru z mniejszym błędem pomiaru, a wyższą trafnością i rzetelnością[18],
  • wykorzystanie testów lub struktur badania, które mają z natury wyższą moc statystyczną, takich jak metody bayesowskie, testy parametryczne, prerejestrowane testy hipotez jednostronnych, oraz badania w schemacie wewnątrzgrupowym (pomiary powtarzane; Rouder i Haaf określili jednak, że generalnie lepiej zwiększać liczbę uczestników niż powtórzeń)[16][19].

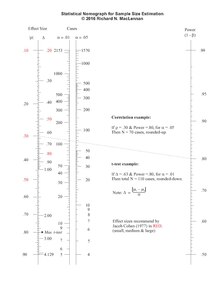
Narzędzia do obliczania

[edytuj | edytuj kod]

Większość pakietów statystycznych, takich jak SPSS lub darmowe i otwarte oprogramowanie R posiada funkcje obliczania mocy. Przykładowym, najczęściej spotykanym narzędziem służącym specjalnie do tego celu jest darmowy program G*Power[20]. Programy te pozwalają na obliczanie mocy przed badaniem (a priori), w celu określenia wielkości próby potrzebnej do osiągnięcia pożądanego poziomu mocy, jak również po badaniu (post hoc), np. na potrzeby kontroli jakości.

Przeglądy mocy statystycznej dziedzin nauki

[edytuj | edytuj kod]

Statystycy regularnie publikują rezultaty badań przeglądowych dla różnych dziedzin nauki, z których wynika że przeciętna moc badań jest dużo niższa niż rekomendowany poziom 0,8. Przykładowo, w przeglądzie dla neuronauki z 2013 r. obejmującym 49 meta-analiz i 730 osobnych badań, mediana mocy dla obserwowanych efektów wyniosła zaledwie 21%[21]. W przeglądzie badań psychologicznych z 1990 r., moc wyniosła 17% dla małych, i 57% dla średnich efektów[22] – a takie wielkości efektu najczęściej spotyka się w tej dziedzinie[23][24]. Analiza z 2006 r. obejmująca publikacje informatyczne wykazała moc 11% dla małych, i 36% dla średnich efektów[25]. Meta-przegląd 8 tysięcy badań psychologicznych z 2018 określił medianę ich mocy na poziomie 36%; tylko 8% badań osiągnęło rekomendowaną moc 0,8[26].

Konsekwencje niskiej mocy badań

[edytuj | edytuj kod]

Nawet jeśli badacz projektuje badanie o mocy na rekomendowanym poziomie 0,8, powinien spodziewać się, że badając rzeczywiście występujące zjawisko, spotka się z nieudanymi replikacjami. Przykładowo, przy tej mocy, prawdopodobieństwo przyjęcia hipotezy alternatywnej za każdym razem w trzech replikacjach wynosi bowiem tylko 0,8³ ≈ 51,2%. W sytuacji w której moc badań jest bliższa poziomu α=0,05 niż 0,8, należy się spodziewać, że znaczna część wyników istotnych statystycznie jest fałszywa, natomiast nieznana część wyników nieistotnych to odrzucone pochopnie prawidłowe hipotezy. Oznacza to zniekształcenie obrazu rzeczywistości, jaki sugeruje treść opublikowanych badań, zwłaszcza w połączeniu z „efektem szuflady”.

Testy o niskiej mocy przeszacowują ponadto obserwowaną wielkość efektu prawdziwych zjawisk, ponieważ istotność statystyczną jest częściej osiągana w próbach, w których z naturalnej wariancji zjawisko występuje z większą siłą[27]. Istotność osiągają częściej nawet oszacowania o przeciwnym znaku niż realny efekt[5].

W świetle m.in. powyższych problemów, Ioannidis zadeklarował w publikacji z 2005 r., że większość publikacji naukowych może być błędna[28]. W ostatnich latach statystycy, wydawcy czasopism naukowych oraz towarzystwa zawodowe, takie jak Amerykańskie Towarzystwo Psychologiczne, rekomendują, a w niektórych wypadkach nawet wymagają od badaczy dokumentowania decyzji dotyczących wielkości próby, ze względu na systematyczny problem z niewystarczającą mocą badań[29]. Zaleca się też używanie przedziałów ufności, raportowanie wielkości efektów, prerejestrację planów badawczych, przeprowadzanie replikacji naukowych, stosowanie technik metaanalitycznych, oraz innych metod zwiększających jakość nauki[30][31][32].

Zobacz też

[edytuj | edytuj kod]

Przypisy

[edytuj | edytuj kod]
  1. ↑ a b c d Cohen, Jacob, 1923-1998., Statistical power analysis for the behavioral sciences, L. Erlbaum Associates, 1988, ISBN 0-8058-0283-5, OCLC 17877467.
  2. ↑ David Colquhoun, Lectures on Biostatistics An Introduction to Statistics with Applications in Biology and Medicine, Oxford University Press, 1971, s. 96-97 [dostęp 2017-01-09].
  3. ↑ Jacob Cohen, A power primer., „Psychological Bulletin”, 112 (1), 1992, s. 155–159, DOI: 10.1037/0033-2909.112.1.155, ISSN 1939-1455 [dostęp 2017-01-31] (ang.).
  4. ↑ Marcus R. Munafò i inni, Power failure: why small sample size undermines the reliability of neuroscience, „Nature Reviews Neuroscience”, 14 (5), 2013, s. 365–376, DOI: 10.1038/nrn3475, ISSN 1471-0048 [dostęp 2019-03-31] (ang.).
  5. ↑ a b c Andrew Gelman, John Carlin, Beyond Power Calculations: Assessing Type S (Sign) and Type M (Magnitude) Errors, „Perspectives on Psychological Science”, 9 (6), 2014, s. 641–651, DOI: 10.1177/1745691614551642, ISSN 1745-6916 [dostęp 2019-03-31] (ang.).
  6. ↑ Andrew Gelman, You need 16 times the sample size to estimate an interaction than to estimate a main effect « Statistical Modeling, Causal Inference, and Social Science [online], statmodeling.stat.columbia.edu [dostęp 2019-03-31].
  7. ↑ Eric-Jan Wagenmakers i inni, A power fallacy, „Behavior Research Methods”, 47 (4), 2015, s. 913–917, DOI: 10.3758/s13428-014-0517-4, ISSN 1554-3528 [dostęp 2019-03-31] (ang.).
  8. ↑ Why you should think of statistical power as a curve [online], PsychBrief, 14 grudnia 2017 [dostęp 2019-03-31] (ang.).
  9. ↑ Felix D. Schönbrodt, Marco Perugini, At what sample size do correlations stabilize?, „Journal of Research in Personality”, 47 (5), 2013, s. 609–612, DOI: 10.1016/j.jrp.2013.05.009 [dostęp 2019-03-31] (ang.).
  10. ↑ Daniël Lakens, Equivalence Tests: A Practical Primer for t Tests, Correlations, and Meta-Analyses, „Social Psychological and Personality Science”, 8 (4), 2017, s. 355–362, DOI: 10.1177/1948550617697177, ISSN 1948-5506, PMID: 28736600, PMCID: PMC5502906 [dostęp 2019-03-31] (ang.).
  11. ↑ Farid Anvari, Daniel Lakens, Using Anchor-Based Methods to Determine the Smallest Effect Size of Interest, DOI: 10.31234/osf.io/syp5a [dostęp 2019-03-31].
  12. ↑ Casper Albers, Daniël Lakens, When power analyses based on pilot data are biased: Inaccurate effect size estimators and follow-up bias, „Journal of Experimental Social Psychology”, 74, 2018, s. 187–195, DOI: 10.1016/j.jesp.2017.09.004 [dostęp 2019-03-31] (ang.).
  13. ↑ John M Hoenig, Dennis M Heisey, The Abuse of Power: The Pervasive Fallacy of Power Calculations for Data Analysis, „The American Statistician”, 55 (1), 2001, s. 19–24, DOI: 10.1198/000313001300339897, ISSN 0003-1305 [dostęp 2019-03-31] (ang.).
  14. ↑ Jeehyoung Kim, Bong Soo Seo, How to Calculate Sample Size and Why, „Clinics in Orthopedic Surgery”, 5 (3), 2017, s. 235–242, DOI: 10.4055/cios.2013.5.3.235, ISSN 2005-291X, PMID: 24009911, PMCID: PMC3758995 [dostęp 2017-01-31].
  15. ↑ Helena Chmura Kraemer i inni, Caution Regarding the Use of Pilot Studies to Guide Power Calculations for Study Proposals, „Archives of General Psychiatry”, 63 (5), 2006, DOI: 10.1001/archpsyc.63.5.484, ISSN 0003-990X [dostęp 2017-01-31] (ang.).
  16. ↑ a b Daniël Lakens, Calculating and reporting effect sizes to facilitate cumulative science: a practical primer for t-tests and ANOVAs, „Frontiers in Psychology”, 4, 2013, DOI: 10.3389/fpsyg.2013.00863, ISSN 1664-1078, PMID: 24324449, PMCID: PMC3840331 [dostęp 2017-01-31].
  17. ↑ David M. Erceg-Hurn, Vikki M. Mirosevich, Modern robust statistical methods: an easy way to maximize the accuracy and power of your research, „The American Psychologist”, 63 (7), 2008, s. 591–601, DOI: 10.1037/0003-066X.63.7.591, ISSN 0003-066X, PMID: 18855490 [dostęp 2017-02-01].
  18. ↑ Kanyongo i inni, Reliability and Statistical Power: How Measurement Fallibility Affects Power and Required Sample Sizes for Several Parametric and Nonparametric Statistics, „Journal of Modern Applied Statistical Methods”, 6 (1), 2007 [dostęp 2017-01-31] (ang.).
  19. ↑ Jeffrey N. Rouder, Julia M. Haaf, Power, Dominance, and Constraint: A Note on the Appeal of Different Design Traditions, „Advances in Methods and Practices in Psychological Science”, 1 (1), 2018, s. 19–26, DOI: 10.1177/2515245917745058, ISSN 2515-2459 [dostęp 2019-03-31] (ang.).
  20. ↑ Franz Faul i inni, Statistical power analyses using G*Power 3.1: Tests for correlation and regression analyses, „Behavior Research Methods”, 41 (4), 2009, s. 1149–1160, DOI: 10.3758/BRM.41.4.1149, ISSN 1554-3528 [dostęp 2019-03-31] (ang.).
  21. ↑ Katherine S. Button i inni, Power failure: why small sample size undermines the reliability of neuroscience, „Nature Reviews Neuroscience”, 5, 2013, s. 365–376, DOI: 10.1038/nrn3475, ISSN 1471-003X [dostęp 2017-01-06] (ang.).
  22. ↑ J.S. Rossi, Statistical power of psychological research: what have we gained in 20 years?, „Journal of Consulting and Clinical Psychology”, 5, 1990, s. 646–656, ISSN 0022-006X, PMID: 2254513 [dostęp 2017-01-06].
  23. ↑ Frank A. Bosco i inni, Correlational effect size benchmarks, „The Journal of Applied Psychology”, 2, 2015, s. 431–449, DOI: 10.1037/a0038047, ISSN 1939-1854, PMID: 25314367 [dostęp 2017-01-06].
  24. ↑ F.D. Richard, Charles F. Bond, Juli J. Stokes-Zoota, One Hundred Years of Social Psychology Quantitatively Described., „Review of General Psychology”, 4, 2003, s. 331–363, DOI: 10.1037/1089-2680.7.4.331, ISSN 1939-1552 [dostęp 2017-01-06].
  25. ↑ Tore Dybå, Vigdis By Kampenes, Dag I.K. Sjøberg, A systematic review of statistical power in software engineering experiments, „Information and Software Technology”, 8, 2006, s. 745–755, DOI: 10.1016/j.infsof.2005.08.009 [dostęp 2017-01-06].
  26. ↑ T.D. Stanley, Evan C. Carter, Hristos Doucouliagos, What meta-analyses reveal about the replicability of psychological research., „Psychological Bulletin”, 144 (12), 2018, s. 1325–1346, DOI: 10.1037/bul0000169, ISSN 1939-1455 [dostęp 2019-03-31] (ang.).
  27. ↑ John P.A. Ioannidis, Why most discovered true associations are inflated, „Epidemiology (Cambridge, Mass.)”, 5, 2008, s. 640–648, DOI: 10.1097/EDE.0b013e31818131e7, ISSN 1531-5487, PMID: 18633328 [dostęp 2017-01-06].
  28. ↑ John P.A. Ioannidis, Why Most Published Research Findings Are False, „PLOS Medicine”, 8, 2005, e124, DOI: 10.1371/journal.pmed.0020124, ISSN 1549-1676, PMID: 16060722, PMCID: PMC1182327 [dostęp 2017-01-06].
  29. ↑ Statistical methods in psychology journals: Guidelines and explanations., „American Psychologist”, 8, 1999, DOI: 10.1037/0003-066X.54.8.594, ISSN 1935-990X [dostęp 2017-01-06].
  30. ↑ D. Lakens, E.R.K. Evers, Sailing From the Seas of Chaos Into the Corridor of Stability: Practical Recommendations to Increase the Informational Value of Studies, „Perspectives on Psychological Science”, 3, 2014, s. 278–292, DOI: 10.1177/1745691614528520 [dostęp 2017-01-06] (ang.).
  31. ↑ Open Science Collaboration, An Open, Large-Scale, Collaborative Effort to Estimate the Reproducibility of Psychological Science, „Perspectives on Psychological Science”, 6, 2012, s. 657–660, DOI: 10.1177/1745691612462588 [dostęp 2017-01-06] (ang.).
  32. ↑ Daniel Lakens, Calculating and reporting effect sizes to facilitate cumulative science: a practical primer for t-tests and ANOVAs, „Cognition”, 4, 2013, s. 863, DOI: 10.3389/fpsyg.2013.00863, PMID: 24324449, PMCID: PMC3840331 [dostęp 2017-01-06].

Bibliografia

[edytuj | edytuj kod]
Źródło: „https://pl.wikipedia.org/w/index.php?title=Moc_testu&oldid=74795764”