Funzione φ di Eulero

I primi mille valori di $\varphi$

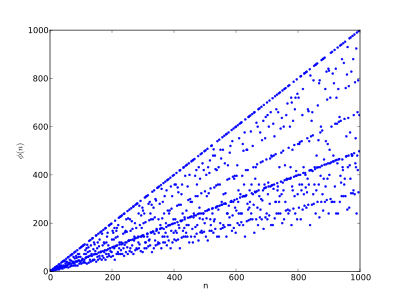
In matematica, la funzione φ di Eulero o semplicemente funzione di Eulero o toziente, è una funzione definita, per ogni intero positivo $n$, come il numero degli interi compresi tra $1$ e $n$ che sono coprimi con $n$. Ad esempio, $\varphi (8)=4$ poiché i numeri coprimi di 8 sono quattro: 1, 3, 5, 7. Deve il suo nome al matematico svizzero Eulero, che per primo la descrisse.

La funzione $\varphi (n)$ è una funzione molto importante nella teoria dei numeri, principalmente perché è la cardinalità del gruppo moltiplicativo degli interi modulo $n$, più precisamente è l'ordine del gruppo moltiplicativo dell'anello $\mathbb {Z} /n\mathbb {Z}$ (vedere aritmetica modulare). Questo fatto, unito con il teorema di Lagrange, dimostra il teorema di Eulero: se $a$ è un numero coprimo con $n$, allora:

$a^{\varphi (n)}\equiv 1\mod n$

Moltiplicatività

La funzione φ di Eulero è moltiplicativa: per ogni coppia di interi a e b tali che MCD(a, b)=1, si ha:

$\varphi (ab)=\varphi (a)\varphi (b)$

Questo fatto può essere dimostrato in molti modi: ad esempio, si può osservare che un numero è coprimo con ab se e solo se è coprimo sia con a sia con b. Infatti, dato un x coprimo con ab, questo non ha fattori in comune con ab, e quindi non ha fattori in comune né con a né con b; viceversa, se x è coprimo con a e con b, ed esistesse un primo p che divide sia ab sia x, p dovrebbe dividere, per il lemma di Euclide, almeno uno tra a e b, e quindi x non può esser coprimo con entrambi.

Una volta dimostrato questo, si osserva che ogni coppia (y, z), con $y\in \mathbb {Z} _{a}$ e $z\in \mathbb {Z} _{b}$ corrisponde a uno e un solo elemento $w\in \mathbb {Z} _{ab}$ (o, per essere più formali, che esiste un isomorfismo tra gli anelli $\mathbb {Z} _{a}\times \mathbb {Z} _{b}$ e $\mathbb {Z} _{ab}$). Quindi il numero di elementi coprimi con ab è uguale a quello delle coppie (y, z) dove y è coprimo con a e z con b.

Per definizione i primi sono $\varphi (a)$ e i secondi $\varphi (b)$, e quindi in definitiva ci sono $\varphi (a)\varphi (b)$ elementi coprimi con ab che è per definizione il valore $\varphi (ab)$

Calcolo della funzione

Un'espressione per la funzione è la seguente:

$\varphi (n)=n\cdot \left[\left(1-{\frac {1}{p_{1}}}\right)\left(1-{\frac {1}{p_{2}}}\right)\cdots \left(1-{\frac {1}{p_{r}}}\right)\right]=n\prod _{p\mid n}\left(1-{\frac {1}{p}}\right)$

dove i $p_{i}$ sono tutti i primi che compongono la fattorizzazione di n.

Dimostrazione

Mostriamo innanzitutto che, se p è un numero primo, allora $\varphi (p^{k})=(p-1)p^{k-1}$ per ogni $k>0$.

Per fare ciò, troviamo tutti i numeri m minori o uguali a $p^{k}$ per i quali $MCD(p^{k},m)\neq \ 1$. Ciò equivale a dire che m deve avere dei fattori in comune con $p^{k}$. Ma p è primo, quindi se m ha dei fattori in comune con p, questi devono essere multipli di una potenza di p. Quindi tutti i possibili valori di m sono $p,2p,3p,\ldots ,p^{k-1}\cdot p$. Questi numeri sono $p^{k-1}$, e sono tutti i numeri che non sono coprimi con $p^{k}$. Tutti i numeri minori o uguali a $p^{k}$ sono $p^{k}$, quindi i numeri primi con $p^{k}$ minori di $p^{k}$ sono i restanti $p^{k}-p^{k-1}$.

Quindi $\varphi (p^{k})=p^{k}-p^{k-1}=(p-1)p^{k-1}$

Utilizzando il teorema fondamentale dell'aritmetica possiamo fattorizzare qualsiasi numero $n$ in un prodotto di numeri primi elevati a una certa potenza:

$n=p_{1}^{k_{1}}p_{2}^{k_{2}}\ldots p_{r}^{k_{r}}$

dove i $p_{i}$ sono numeri primi distinti, e ogni $k_{i}>0$

Quindi $\varphi (n)=\varphi (p_{1}^{k_{1}}p_{2}^{k_{2}}\ldots p_{r}^{k_{r}})$

Ora, poiché $\varphi$ è moltiplicativa possiamo espandere la funzione:

$\varphi (n)=\varphi (p_{1}^{k_{1}})\varphi (p_{2}^{k_{2}})\ldots \varphi (p_{r}^{k_{r}})=p_{1}^{k_{1}-1}(p_{1}-1)\cdot p_{2}^{k_{2}-1}(p_{2}-1)\cdots p_{r}^{k_{r}-1}(p_{r}-1)$

(La funzione è moltiplicativa tra due numeri se e solo se essi sono primi tra loro. Nel nostro caso, i numeri $p_{i}$ sono tutti primi, e quindi primi tra loro)

La formula può essere riscritta in una forma più compatta:

$\varphi (n)=n\cdot \left[\left(1-{\frac {1}{p_{1}}}\right)\left(1-{\frac {1}{p_{2}}}\right)\cdots \left(1-{\frac {1}{p_{r}}}\right)\right]=n\prod _{p\mid n}\left(1-{\frac {1}{p}}\right)$

Andamento asintotico

La scrittura prima trovata permette inoltre di dimostrare che i valori della funzione φ possono essere arbitrariamente piccoli rispetto a n (cioè il rapporto $\varphi (n)/n$ è minore di qualunque $\epsilon$ per qualche valore di n): estendendo infatti il prodotto a tutti i primi, si ottiene

${\frac {p_{1}-1}{p_{1}}}{\frac {p_{2}-1}{p_{2}}}\cdots =\left[{\frac {p_{1}}{p_{1}-1}}\cdot {\frac {p_{2}}{p_{2}-1}}\cdots \right]^{-1}$

Quella tra parentesi è la scrittura del prodotto di Eulero della funzione zeta di Riemann per s=1, cioè la somma

${\frac {1}{1}}+{\frac {1}{2}}+{\frac {1}{3}}+\cdots$

ovvero la serie armonica, che diverge. Quindi il suo inverso è infinitesimale, e la successione

${\frac {\varphi (n)}{n}}$

diventa arbitrariamente vicina a 0.

Altre proprietà

• Il numero φ(n) è anche pari al numero di generatori del gruppo ciclico C_n. Da ciascun elemento di C_n si può generare un sottogruppo ciclico C_d dove d divide n (la notazione è d|n), ottenendo:

$\sum _{d\mid n}\varphi (d)=n$

dove la somma è estesa a tutti i divisori d di n.

Si può ora utilizzare la funzione di inversione di Möbius per invertire questa somma e ottenere un'altra formula per la φ(n):

$\varphi (n)=\sum _{d\mid n}d\cdot \mu \left({n \over d}\right)$

dove $\mu$ è l'usuale funzione di Möbius definita sugli interi positivi.

• Abbiamo inoltre che, se n è un numero primo:

$\varphi (n)=n-1$

Dato che, ovviamente, ogni numero minore di n gli è coprimo, essendo n primo.

• Esiste una sequenza di valori di n tale che

$\varphi (n)=\varphi (n+1)$

i primi sono 1, 3, 15, 104, 164, 194, 255, 495, 584, 975, ... (sequenza A001274 dell'OEIS).

• Esiste un solo numero $n<10^{10}$ tale che

$\varphi (n)=\varphi (n+1)=\varphi (n+2)$

e si tratta di 5186, per il quale si ha infatti

$\varphi (5186)=\varphi (5186+1)=\varphi (5186+2)=2^{5}\cdot 3^{4}$

• Esiste una progressione aritmetica di ragione 30 composta da sei numeri, che generano tutti lo stesso valore di φ  :

$\varphi (583200)=\varphi (583230)=\varphi (583260)=\,$

$\varphi (583290)=\varphi (583320)=\varphi (583350)=\,$

$=155520=2^{7}\cdot 3^{5}\cdot 5$

• $a\mid b$ implica $\varphi (a)\mid \varphi (b)$
• $\varphi (n)$ è pari per $n\geq 3$. Inoltre, se n ha r fattori primi distinti dispari, allora $2^{r}\mid \varphi (n)$

Funzione generatrice

Le due funzioni generatrici presentate qui sono entrambe conseguenze del fatto che

$\sum _{d|n}\varphi (d)=n.$

Una serie di Dirichlet che genera la φ(n) è

$\sum _{n=0}^{\infty }{\frac {\varphi (n)}{n^{s}}}={\frac {\zeta (s-1)}{\zeta (s)}}$

dove $\zeta$ è la funzione zeta di Riemann. Ciò deriva da quanto segue:

$\zeta (s)\sum _{f=1}^{\infty }{\frac {\varphi (f)}{f^{s}}}=\left(\sum _{g=1}^{\infty }{\frac {1}{g^{s}}}\right)\left(\sum _{f=1}^{\infty }{\frac {\varphi (f)}{f^{s}}}\right)$

$\left(\sum _{g=1}^{\infty }{\frac {1}{g^{s}}}\right)\left(\sum _{f=1}^{\infty }{\frac {\varphi (f)}{f^{s}}}\right)=\sum _{h=1}^{\infty }\left(\sum _{fg=h}1\cdot \varphi (g)\right){\frac {1}{h^{s}}}$

$\sum _{h=1}^{\infty }\left(\sum _{fg=h}\varphi (g)\right){\frac {1}{h^{s}}}=\sum _{h=1}^{\infty }\left(\sum _{d|h}\varphi (d)\right){\frac {1}{h^{s}}}$

$\sum _{h=1}^{\infty }\left(\sum _{d|h}\varphi (d)\right){\frac {1}{h^{s}}}=$$\sum _{h=1}^{\infty }{\frac {h}{h^{s}}}$

$\sum _{h=1}^{\infty }{\frac {h}{h^{s}}}=\zeta (s-1).$

La funzione generatrice di una serie di Lambert è

$\sum _{n=1}^{\infty }{\frac {\varphi (n)q^{n}}{1-q^{n}}}={\frac {q}{(1-q)^{2}}}$

che converge per |q| < 1. Ciò deriva da

$\sum _{n=1}^{\infty }{\frac {\varphi (n)q^{n}}{1-q^{n}}}=\sum _{n=1}^{\infty }\varphi (n)\sum _{r=1}^{\infty }q^{rn}$

che è

$\sum _{k=1}^{\infty }q^{k}\sum _{n|k}\varphi (n)=\sum _{k=1}^{\infty }kq^{k}={\frac {q}{(1-q)^{2}}}.$

Disuguaglianze

Alcune disuguaglianze riguardanti la funzione $\varphi$ sono:

$\varphi (n)>{\frac {n}{e^{\gamma }\;\log \log n+{\frac {3}{\log \log n}}}}$ per n > 2, dove γ è la costante di Eulero-Mascheroni,

$\varphi (n)\geq {\sqrt {\frac {n}{2}}}$ per n > 0,

e

$\varphi (n)\geq {\sqrt {n}}{\text{ per }}n>6.$

Se n è composto abbiamo

$\varphi (n)\leq n-{\sqrt {n}}$

Per ogni numero pari 2n, dove 2n non è della forma 2^k, abbiamo

$\varphi (2n)\leq n-1$

Se invece 2n è pari e della forma 2^k, abbiamo

$\varphi (2n)=n$

Per valori di n arbitrariamente grandi, si avrà

$\liminf {\frac {\varphi (n)}{n}}=0$ e $\limsup {\frac {\varphi (n)}{n}}=1.$

Un paio di disuguaglianze che combinano la funzione $\varphi$ con la funzione $\sigma$ sono:

${\frac {6n^{2}}{\pi ^{2}}}<\varphi (n)\sigma (n)<n^{2}{\mbox{ per }}n>1.$

Alcuni valori della funzione

$\varphi (n)$	0	1	2	3	4	5	6	7	8	9
0+		1	1	2	2	4	2	6	4	6
10+	4	10	4	12	6	8	8	16	6	18
20+	8	12	10	22	8	20	12	18	12	28
30+	8	30	16	20	16	24	12	36	18	24
40+	16	40	12	42	20	24	22	46	16	42
50+	20	32	24	52	18	40	24	36	28	58
60+	16	60	30	36	32	48	20	66	32	44
70+	24	70	24	72	36	40	36	60	24	78
80+	32	54	40	82	24	64	42	56	40	88
90+	24	72	44	60	46	72	32	96	42	60

Bibliografia

• Luca Barbieri Viale, Teorema 4.27, Che cos'è un numero ? Raffaello Cortina, 2013, ISBN 978-88-6030-604-3
• Tom M. Apostol (1976): Introduction to Analytic Number Theory, Springer-Verlag, New York. ISBN 0-387-90163-9, (Chapter 2)
• H. Davenport, Aritmetica superiore, Zanichelli, Bologna, 1994, ISBN 88-08-09154-6 - Capitolo II.4

Voci correlate

• Aritmetica modulare
• Interi coprimi
• Nontotiente
• Noncototiente
• Funzione aritmetica
• Teorema di Eulero (aritmetica modulare)
• Campo ciclotomico

Altri progetti

Altri progetti

• Wikimedia Commons

• Wikimedia Commons contiene immagini o altri file sulla funzione φ di Eulero

Collegamenti esterni

• Eulero, funzione toziente di, in Enciclopedia della Matematica, Istituto dell'Enciclopedia Italiana, 2013.
• (EN) Euler phi function, su Enciclopedia Britannica, Encyclopædia Britannica, Inc.
• (EN) Eric W. Weisstein, Totient Function, su MathWorld, Wolfram Research.
• (EN) Euler function, su Encyclopaedia of Mathematics, Springer e European Mathematical Society.
• (EN) Euler Totient Function, su functions.wolfram.com.
• Kirby Urner, Computing totient function in Python and scheme, (2003)
• JavaScript totient calculator, su www25.brinkster.com. URL consultato il 14 gennaio 2011 (archiviato dall'url originale il 15 giugno 2011).
• Miyata, Daisuke & Yamashita, Michinori, Derived logarithmic function of Euler's function
• Bordellès, Olivier, Numbers prime to q in $[1,n]$
• Plytage, Loomis, Polhill Summing Up The Euler Phi Function Archiviato il 23 luglio 2011 in Internet Archive.
• Fabrizio Romano, Python implementation