Eulerova funkcija je funkcija koja svakom prirodnom broju
n
{\displaystyle n}
relativno prostih brojeva s
n
{\displaystyle n}
n
{\displaystyle n}
n
=
1
{\displaystyle n=1}
φ
(
n
)
{\displaystyle \varphi {(n)}}
[ 1]
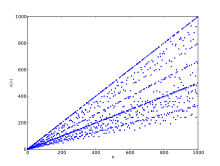
Prvih tisuću vrijednosti Eulerove funkcije. Točke na gornjoj liniji predstavljaju vrijednosti za proste brojeve. Primjerice, vrijedi
φ
(
2
)
=
1
,
φ
(
6
)
=
2
,
φ
(
11
)
=
10
,
{\displaystyle \varphi (2)=1,\varphi (6)=2,\varphi (11)=10,}
Uočimo da je
φ
(
1
)
=
1
,
φ
(
p
)
=
p
−
1
{\displaystyle \varphi (1)=1,\varphi (p)=p-1}
p
{\displaystyle p}
Skup relativno prostih brojeva s
n
{\displaystyle n}
{
1
,
2
,
.
.
.
n
}
{\displaystyle \{1,2,...n\}}
S
n
{\displaystyle S_{n}}
Ovu je funkciju 1763. uveo znameniti švicarski matematičar Leonhard Euler .
▪Eulerova funkcija je multiplikativna , odnosno vrijedi
φ
(
1
)
=
1
{\displaystyle \varphi {(1)}=1}
φ
(
m
n
)
=
φ
(
m
)
φ
(
n
)
{\displaystyle \varphi {(mn)}=\varphi (m)\varphi (n)}
[ 2]
▪
φ
(
p
α
)
=
p
α
−
p
α
−
1
,
{\displaystyle \varphi (p^{\alpha })=p^{\alpha }-p^{\alpha -1},}
▪ Vrijedi
φ
(
n
)
=
n
∏
p
∣
n
(
1
−
1
p
)
,
{\displaystyle \varphi (n)=n\prod _{p\mid n}\left(1-{\frac {1}{p}}\right),}
▪ Vrijedi
∑
d
∣
n
φ
(
d
)
=
n
{\displaystyle \sum _{d\mid n}\varphi (d)=n}
Gaussova lema o Eulerovoj funkciji ).
Uzmimo
n
=
20.
{\displaystyle n=20.}
S
20
{\displaystyle S_{20}}
S
20
=
{
1
,
3
,
7
,
9
,
11
,
13
,
17
,
19
}
.
{\displaystyle S_{20}=\{1,3,7,9,11,13,17,19\}.}
Uočimo da je
1
+
19
=
3
+
17
=
7
+
13
=
9
+
11
=
20.
{\displaystyle 1+19=3+17=7+13=9+11=20.}
Pretpostavljamo da struktura skupa
S
n
=
{
k
1
=
1
,
k
2
,
.
.
.
,
k
r
=
n
−
1
}
{\displaystyle S_{n}=\{k_{1}=1,k_{2},...,k_{r}=n-1\}}
k
i
+
k
n
−
i
=
n
,
∀
i
=
1
,
2
,
.
.
.
,
r
.
{\displaystyle k_{i}+k_{n-i}=n,\forall i=1,2,...,r.}
Sada ćemo tvrdnju ovog naslućivanja i dokazati. Neka je
k
∈
N
{\displaystyle k\in \mathbb {N} }
M
(
k
,
n
)
=
1.
{\displaystyle M(k,n)=1.}
M
(
n
−
k
,
n
)
=
1.
{\displaystyle M(n-k,n)=1.}
M
(
n
−
k
,
n
)
=
d
>
1.
{\displaystyle M(n-k,n)=d>1.}
d
|
n
,
d
|
n
−
k
.
{\displaystyle d|n,d|n-k.}
n
−
k
{\displaystyle n-k}
d
{\displaystyle d}
d
|
k
.
{\displaystyle d|k.}
d
=
1
,
{\displaystyle d=1,}
Zato je za
n
≥
3
{\displaystyle n\geq 3}
S
n
{\displaystyle S_{n}}
φ
(
1
)
=
φ
(
2
)
=
1.
{\displaystyle \varphi (1)=\varphi (2)=1.}
S
n
{\displaystyle S_{n}}
[ uredi | uredi kôd ] Isto tako, treba uočiti da vrijedi sljedeće.
Ako je dakle
n
=
2
k
{\displaystyle n=2k}
S
2
n
{\displaystyle S_{2n}}
S
2
n
{\displaystyle S_{2n}}
S
10
=
{
1
,
3
,
7
,
9
}
{\displaystyle S_{10}=\{1,3,7,9\}}
S
12
=
{
1
,
5
,
7
,
11
}
{\displaystyle S_{12}=\{1,5,7,11\}}
Ako je pak
n
=
2
k
+
1
{\displaystyle n=2k+1}
S
2
n
{\displaystyle S_{2n}}
k
,
k
+
1
{\displaystyle k,k+1}
S
2
n
{\displaystyle S_{2n}}
1
{\displaystyle 1}
M
(
2
k
+
1
,
k
)
=
M
(
2
k
+
1
,
k
+
1
)
=
1.
{\displaystyle M(2k+1,k)=M(2k+1,k+1)=1.}
M
(
k
+
(
k
+
1
)
,
k
)
=
d
{\displaystyle M(k+(k+1),k)=d}
d
|
k
+
1
{\displaystyle d|k+1}
d
|
k
,
d
|
k
+
1
{\displaystyle d|k,d|k+1}
d
=
1
{\displaystyle d=1}
M
(
k
,
k
+
1
)
=
1
{\displaystyle M(k,k+1)=1}
Svojstvo
M
(
2
k
+
1
,
k
+
1
)
=
1
{\displaystyle M(2k+1,k+1)=1}
M
(
2
k
+
1
,
2
k
+
1
−
k
)
=
1
{\displaystyle M(2k+1,2k+1-k)=1}
S
9
=
{
1
,
2
,
4
,
5
,
7
,
8
}
{\displaystyle S_{9}=\{1,2,4,5,7,8\}}
S
15
=
{
1
,
2
,
4
,
7
,
8
,
11
,
13
,
14
}
{\displaystyle S_{15}=\{1,2,4,7,8,11,13,14\}}
↑ Andrej Dujella, Teorija brojeva, Školska knjiga, Zagreb, 2019.
↑ Geometrijski dokaz se može naći na poveznici Eulerova funkcija