Arkhimédészi testek

Az arkhimédészi testek (Arkhimédész-féle poliéderek) sokszimmetriájú, félig szabályosnak is nevezett, konvex testek. Két- vagy többféle szabályos sokszög alkotja a lapjaikat, és csúcsalakzataik is egybevágók (de már nem mindig szabályosak, mint az fönnáll a szabályos testekre). Különböznek tehát a platóni vagy szabályos testektől. Nem soroljuk közéjük a prizmákat és az antiprizmákat sem, mert ezeknek kitüntetett forgástengelyük van.

Nevük eredete

Az arkhimédészi testek a nevüket Arkhimédészről kapták, aki részletesen tárgyalta őket egy elveszett munkájában. A reneszánszban kezdték a művészek ismét nagyra értékelni a tiszta formákat és újra fölfedezték őket. 1620-ban Johannes Kepler tette teljessé az ilyen testek körét, aki együtt tárgyalta őket a prizmákkal és az antiprizmákkal.

Osztályozásuk

13 arkhimédészi test van. (Illetve 15 akkor, ha a tükörképi változatokat is figyelembe vesszük az enantiomorf pároknál). Legegyszerűbb megadni őket a csúcsalakzataikkal: azokkal a szabályos sokszögekkel, amik találkoznak egy csúcsukban. Például a (4,6,8) csúcsalakzat azt jelenti, hogy egy csúcsban egy négyzet, egy szabályos hatszög és egy szabályos nyolcszög találkozik.

A test neve (Csúcsalakzat)	Áttetsző ábrája	Szilárd test ábrája	Kiteregetett hálózatos ábrája	Lapok	Lapok (típusuk szerint)	Élek	Csúcsok	A gömbi szimmetriacsoportok listája
csonkított tetraéder (3.6.6)	(Animation)			8	4 háromszög 4 hatszög	18	12	Td
kuboktaéder (3.4.3.4)	(Animation)			14	8 háromszög 6 négyzet	24	12	Oh
csonkított kocka vagy csonkított hexaéder (3.8.8)	(Animation)			14	8 háromszög 6 nyolcszög	36	24	Oh
csonkított oktaéder (4.6.6)	(Animation)			14	6 négyzet 8 hatszög	36	24	Oh
rombikuboktaéder vagy kis rombikuboktaéder (3.4.4.4)	(Animation)			26	8 háromszög 18 négyzet	48	24	Oh
csonkított kuboktaéder vagy nagy rombikuboktaéder (4.6.8)	(Animation)			26	12 négyzet 8 hatszög 6 nyolcszög	72	48	Oh
pisze kocka vagy pisze hexaéder vagy pisze kuboktaéder (2 királis alak) (3.3.3.3.4)	(Animation) (Animation)			38	32 háromszög 6 négyzet	60	24	O
ikozidodekaéder (3.5.3.5)	(Animation)			32	20 háromszög 12 ötszög	60	30	Ih
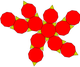
csonkított dodekaéder (3.10.10)	(Animation)			32	20 háromszög 12 tízszög	90	60	Ih
csonkított ikozaéder vagy Fullerén vagy Futball-labda/focilabda (5.6.6)	(Animation)			32	12 ötszög 20 hatszög	90	60	Ih
rombikozidodekaéder vagy kis rombikozidodekaéder (3.4.5.4)	(Animation)			62	20 háromszög 30 négyzet 12 ötszög	120	60	Ih
csonkított ikozidodekaéder vagy nagy rombikozidodekaéder (4.6.10)	(Animation)			62	30 négyzet 20 hatszög 12 tízszög	180	120	Ih
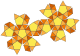
pisze dodekaéder vagy pisze ikozidodekaéder (2 királis alak) (3.3.3.3.5)	(Animation) (Animation)			92	80 háromszög 12 ötszög	150	60	I

A kuboktaéder és az ikozidodekaéder élei uniformok, ezért kváziszabályos testeknek is nevezik őket.

A pisze kockát és a pisze dodekaédert királis testeknek is nevezik, mert előállnak balkezes (latinul: laevo bal, levomorf) alakban is és jobbkezes (latinul: dextro jobb, dextromorf) alakban is. Ha egy háromdimenziós alakzat előáll úgy, mint két alakzat tükörképi párja, akkor ezeket a testeket enantiomorf pároknak nevezzük. Ezt a szakkifejezést főleg a kémiai vegyületekre használják.

Az arkhimédészi testek duális párját alkotó testeket Catalán-testeknek nevezik. Ezeknek a csúcsalakzataik a szabályosak, lapjaik pedig egybevágó, de nem szabályos lapok.

A platoni és arkhimédészi testek periódusos rendszere

Ha megengedjük, hogy a platoni és arkhimédészi testek több példányban is előforduljanak, akkor a duális platoni testek fölhasználásával a következő periodikus táblázatot állíthatjuk össze.

Kocka és oktaéder duális helyzete között három arkhimédészi testet találunk, ha csonkítással jutunk el egyiktől a másikig - itt éppen a kockától az oktaéderig. Hasonlítsuk össze ezt az ábrát a táblázat második sorával.

A platoni és arkhimédészi testek periódusos rendszere. A szabályos testek gömbre vetített változatukban vannak ábrázolva. A snub truncation a pisze testeket jelöli (truncation= csonkítás).

Középen állnak az egyszerű csonkítási sor tagjai. Például a kocka esetén ezek a következők: (A táblázatban is használt Steiner szimbólummal adjuk meg őket): (3,3,3,3), (4,6,6), (3,4,3,4), (3,8,8), (4,4,4). Vagyis az oktaéderrel kezdődő és a kockával végződő (az ábrán a középső) sort adtuk itt meg.

Megszoktuk, hogy az egyedi eseteket soroljuk föl egy-egy készlet megadásánál. Ezt tesszük a platoni testek és az arkhimédészi testek fölsorolásánál is. Azonban a rajtuk lévő sokféle szabályosság lehetővé teszi azt is, hogy tömörebben ábrázoljuk őket, táblázatosan. Ezért azonban árat kell fizetni. Ez az ár pedig az, hogy szerepköre, vagyis a csonkítás alapján, egyféle testnek a sorban többször is meg kell jelennie. Ezen az áron viszont egy szemléletes és jól áttekinthető táblázathoz jutunk és ez nem kis előny.

Kapcsolódó szócikkek

• Szabályos testek
• Szimmetria

Irodalom

• Coxeter, H. S. M. (1987): Geometriák alapjai. Műszaki Könyvkiadó, Budapest
• Coxeter, H. S. M. (1948): Regular Polytopes. Methuen and Co.,
• Coxeter, H. S. M. (1974): Regular Complex Polytopes. Cambridge University Press,
• Fejes Tóth L. (1964): Regular figures. Pergamon Press, 1964, xi+339 pp
• Lakatos I. (1988): Bizonyítások és cáfolatok. Typotex Könyvkiadó, Budapest
• Bérczi Sz. (1979): A szabályos és féligszabályos (platoni és archimedészi) testek és mozaikok periódusos rendszere. Középiskolai Matematikai Lapok. 59. 5. sz. 193-199. old.
• Bérczi Sz. (1990): Szimmetria és struktúraépítés. Egyetemi jegyzet. Tankönyvkiadó, Budapest
• Bérczi Sz. (1992): Sejtautomaták: platoni és archimedészi testeken át. Iskolakultúra. II. 22. sz. 30-43. . (HU ISSN 1215-5233)
• Bérczi Sz. (1993): Double Layered Equation of Motion: Platonic and Archimedean Cellular Automata in the Solution of the Indirect Von Neumann Problem on Sphere for Transformations of regular Tessellations. Acta Mineralogica et Petrographica, Szeged, XXXIX. p. 96-117. (HU ISSN 0365-8006)
• Bérczi Sz. (2003): From the Periodic System of Platonic and Archimedean Solids and Tessellations to the 4D Regular Polyhedra and Tessellations (with Extensions to Some 5D Polytopes). Symmetry: Culture and Science, 11. No. 1-4. p. 125-137. (ISSN 0865-4824)

További információk

• Hargittai István beszélgetése Fejes Tóth Lászlóval, Magyar Tudomány, 2005. március.
• Arkhimédeszi testek írta Eric W. Weisstein, A Wolfram Demonstrations Project egyik demonstrációja.
• Papírmodellek az arkhimédészi testekről és a katalán testekről
• Papírmodellek az Arkhimédeszi testekről
• Az uniform testekről írta Dr. R. Mäder
• Virtuális valóság testek, The Encyclopedia of Polyhedra George W. Hart honlapján.
• Penultimate Moduláris Origami írta James S. Plank
• Interaktív 3D poliéderek Java nyelven.
• Korunkbeli Arkhimédészi testfelületek Tervezte Tom Barber
• Stella: Poliéder Navigátor: Egy olyan szoftver, amelynek segítségével többet is elkészítettek az ezen az oldalon látható ábrákból.
• Kabai Sándor Wolfram Demonstrációs grafikái a féligszabályos testek gömböcös kialakításáról.
• Erdély Dániel spidronizált Arkhimédészi testjei
• Arkhimédészi testek interaktív 3D megjelenítése Archiválva 2013. április 11-i dátummal az Archive.is-en