In a fun experiment I used an Applicos ATX7006A 18 bit AWG to generate a 1 kHz sine wave and used an Analog Devices AD7671 16 bit ADC to digitize the waveform, then coherently captured the digital data and got a nice sine wave out of it. Then I used the Applicos to offset the sine wave by -1 volt forcing it to clip on the lower peak and got this wave and this spectrum.
So why did I get these humps? It's coherently sampled, so it can't be from windowing. Any ideas?
You added offset, signal clipped and now the clipped signal has these harmonics.
To put it in another way, since it's not a sine wave any more, as it has flat portions at the bottom, it can't be represented with a single spectral peak, like the original sine wave.
A clipped sine is a sine that has been multiplied with a rectangle wave, with some constants added:
clip = 0.8
sine = np.sin(wt)
rectangle = sine < clip
clipped = (sine-clip)*rectangle + clip
Visualization:
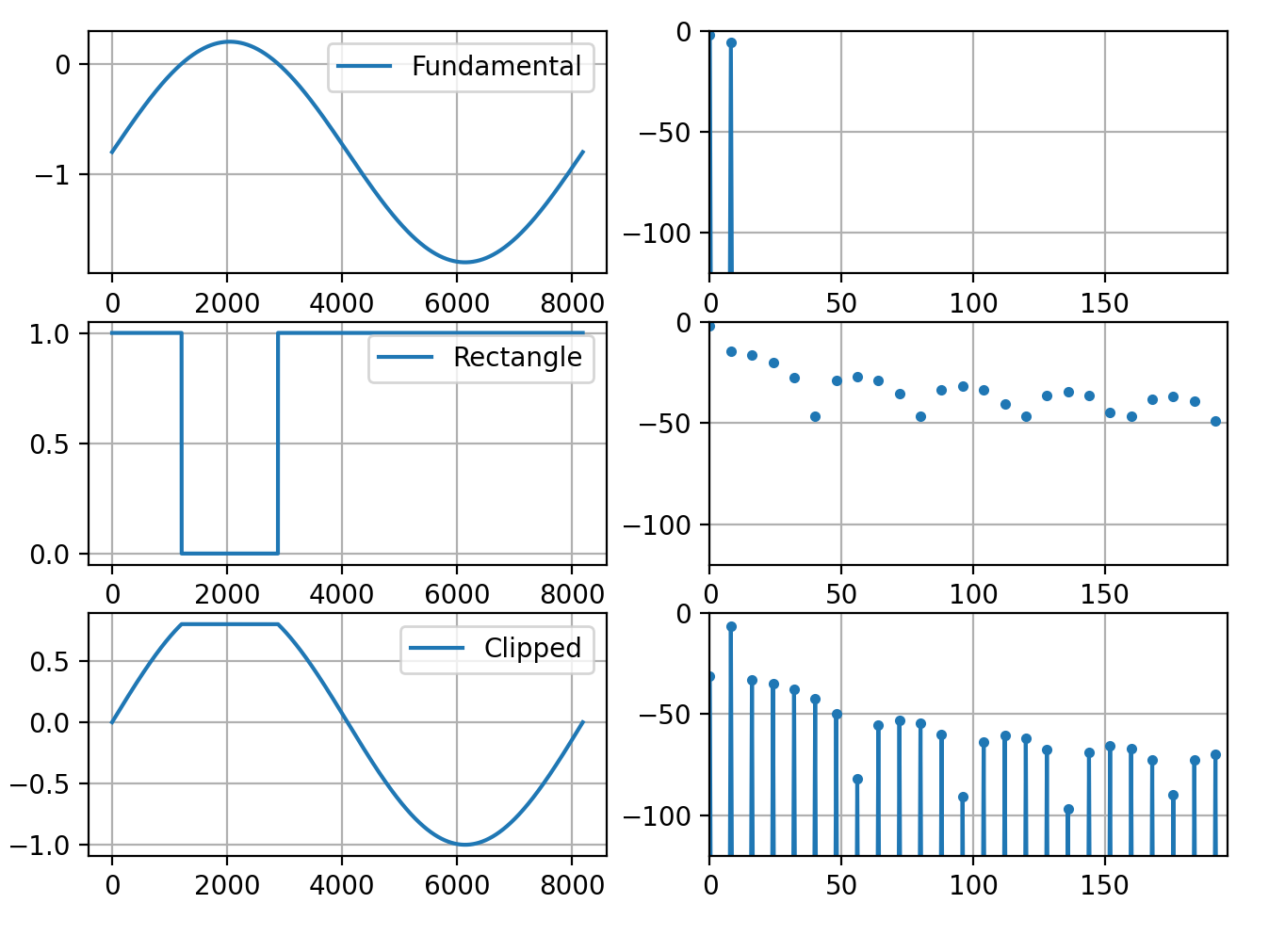
Multiplication in the time domain corresponds to correlation in the frequency domain. So to get the clipped spectrum we take the correlation of :
This means the final spectrum is the weighted sum of two instances of the spectrum of the rectangle wave, with one shifted in frequency.
If the rectangular wave is actually square, with a duty cycle of 50%, it will have smooth harmonic decay without humps. This is the case where the sine is clipped precisely in the center.
But if the rectangular wave is not square, its duty cycle is not 50% because the sine is clipped somewhere else, then its spectrum will have a series of humps, so the result has humps.
Now why does the spectrum of a rectangle wave have humps?
I'll spare the math, but basically a rectangle wave is the product of two square waves having signal values {0,1} with some phase shift applied on each:
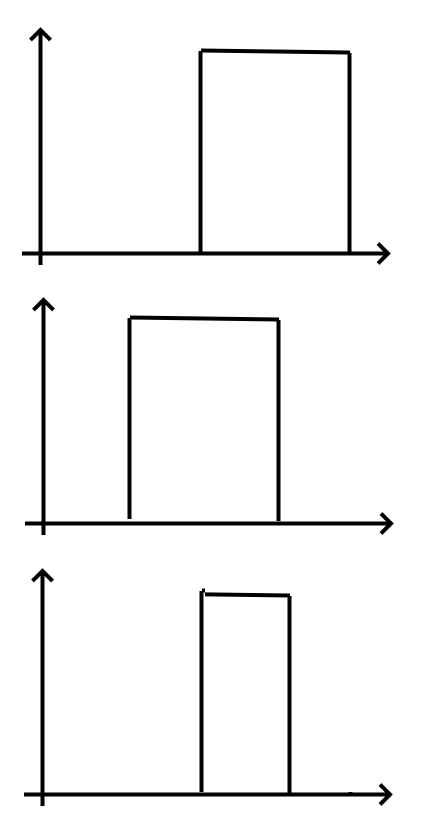
If you multiply the top and middle squares you get the rectangle wave on the bottom... So in the spectrum domain it's the correlation of the spectra of these two square waves, which are identical except for phase shift. The phase shift means harmonics add constructively or destructively depending on the harmonic number, so you get a spectrum with humps that looks like an interference pattern.
Distortion (clipping) produces harmonics but, let's get things into context here; the lowest frequency harmonic is about 35 dB lower than the fundamental and that's about 2% in real numbers magnitude. Anything 60 dB lower is at the 0.1% level or less. Anything 40 dB or lower is no more than the 1% level.
