ディー‐イー‐エー【DEA】
DEA
【英】:DEA (data envelopment analysis)
概要
事業体などの効率性を相対的に評価する手法として, 包絡分析法 (DEA) は1978年にチャーンズ・クーパー・ローズ (Charnes, Cooper and Rhodes) によって提案された. できるだけ少ない入力でできるだけ多くの出力を出す(出力/入力が大)ほど望ましいと考え, 多入力・多出力の場合にも出力の加重和(仮想的出力)と入力の加重和(仮想的入力)をとってそれらの比が大きいほど望ましいとしている. 線形計画法を用いた様々な定式化が提案されている.
詳説
事業体などの意思決定主体 (Decision Making Unit : 略してDMUと呼ばれる) の効率性を相対的に評価する手法として, 包絡分析法(Data Envelopment Analysis:略称DEA)は1978年にアメリカのテキサス大学のCharnes,Cooper and Rhodes [1] によって提案された. 支出と収入の比である収支率は経営効率性を見るための一つの尺度であり, 支出は収入を産み出すための入力, 収入はその結果としての出力とみるとき, 収入/支出(収支率の逆数)が大きい程, 効率が良いと言える. しかし, 入力や出力の数が増え, しかもそれらが必ずしも金額で計量できない場合には効率をどのように評価するか, 適切な尺度を考えなければならない. また, すべての項目 が金額で測れるとしても例えば入力個々の出力に与える影響は異なっており, 単純に(出力の和)/(入力の和)で効率を測ることは適切でないことも多い. そのような場合に仮想的出力として出力の加重和をとり, 仮想的入力として入力の加重和をとってそれらの比で比較することが考えられる. 加重和を取るときに用いるウェイトに説得力を持たせる必要がある. DEAでは評価対象DMUにとって最も有利になるようにウェイトを決めることにしている. しかし, その最も有利になるウェイトを用いても他のDMUよりも仮想的出力/仮想的入力の値が小さければ, そのDMUは効率的でないといわれても仕方がない. このような考え方に基づいて分数計画問題CCR-IR (Charnes, Cooper and Rhodes'Input-oriented Ratio form)モデルおよびそれを線形計画問題に変換したCCRモデル [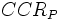 (主問題primal),
(主問題primal), 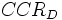 (双対問題dual)モデル]が提案された [1]. Farrellは効率的な生産関数を「入力の組合せが与えられたときに完全に効率的な企業であれば達成するであろう出力」と定義した [2]. その考え方から得られる効率性得点をFarrellは技術的効率性と呼んだ [2]が, それはCCRモデルから得られる効率性得点と一致し, 効率性得点はファレルの効率尺度とも呼ばれる.
(双対問題dual)モデル]が提案された [1]. Farrellは効率的な生産関数を「入力の組合せが与えられたときに完全に効率的な企業であれば達成するであろう出力」と定義した [2]. その考え方から得られる効率性得点をFarrellは技術的効率性と呼んだ [2]が, それはCCRモデルから得られる効率性得点と一致し, 効率性得点はファレルの効率尺度とも呼ばれる.
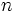 個の事業体(DMU)に関する
個の事業体(DMU)に関する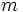 個の入力データ
個の入力データ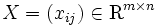 と
と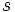 個の出力データ
個の出力データ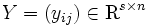 をもとに着目DMU
をもとに着目DMU 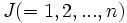 の効率性を測定する
の効率性を測定する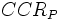 -I(入力指向)モデルは次のように定式化される(このほかの定式化についてはCCRモデルを参照).
-I(入力指向)モデルは次のように定式化される(このほかの定式化についてはCCRモデルを参照).
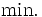 | 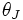 |
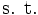 | 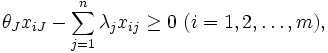 |
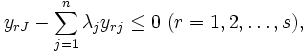 | |
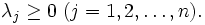 |
このモデルは入力に着目しており, DMU 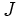 の入力が他と比べて大きく
の入力が他と比べて大きく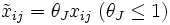 に縮小したいとすると, 制約条件で規定される生産可能集合(
に縮小したいとすると, 制約条件で規定される生産可能集合(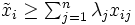 と
と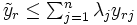 を満たす
を満たす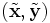 の集合)内でどこまで
の集合)内でどこまで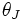 を小さくできるかということを考えている.
を小さくできるかということを考えている.
しかし, 包絡分析法で用いられる入力変数や出力変数の中にはDMUが努力しても改善できないものがある. そのようなDMU自身で制御できない変数を制御不能変数と呼び, それに対して努力により改善可能な変数を制御可能変数と呼ぶ. 制御不能変数が存在する場合には入力, 出力変数に関する制御可能変数番号の集合を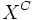 ,
, 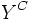 とし, 制御不能変数番号の集合を
とし, 制御不能変数番号の集合を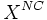 ,
, 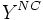 とすると,
とすると, 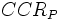 -Iモデルは次のように修正される.
-Iモデルは次のように修正される.
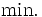 | 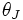 |
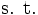 | 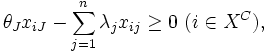 |
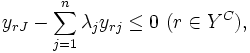 | |
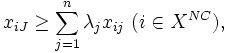 | |
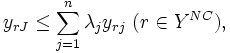 | |
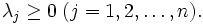 |
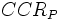 -Iモデルにおける解で
-Iモデルにおける解で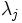 が正となるDMU
が正となるDMU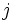 はDMU
はDMU 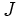 にとって見本とすべきDMUの集合であり, DMU
にとって見本とすべきDMUの集合であり, DMU 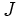 の参照集合と呼ばれる. DMU
の参照集合と呼ばれる. DMU 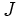 の参照集合の活動の張る凸集合をDMU
の参照集合の活動の張る凸集合をDMU 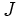 に関する効率的フロンティアと呼ぶ.
に関する効率的フロンティアと呼ぶ. 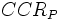 -Iモデルの制約は
-Iモデルの制約は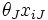 ,
, 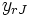 が効率的フロンティアに包みこまれることを意味し, これがData Envelopment Analysis(包絡分析法)の由来となっている(すなわち, [3]では
が効率的フロンティアに包みこまれることを意味し, これがData Envelopment Analysis(包絡分析法)の由来となっている(すなわち, [3]では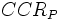 -Iモデルを主問題と捕らえている[
-Iモデルを主問題と捕らえている[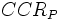 -I の下付きの
-I の下付きの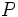 ]). またすべてのDMUの効率的フロンティアで形成される包絡面に包みこまれた領域が生産可能領域である. (包絡面全体を効率的フロンティアということもある. )
]). またすべてのDMUの効率的フロンティアで形成される包絡面に包みこまれた領域が生産可能領域である. (包絡面全体を効率的フロンティアということもある. )
DEAのモデルとしてはいろいろな拡張が試みられている. たとえば, 規模の収穫に着目したり, カテゴリ変数に対処できるモデル, コストを考慮したモデル, 仮想的入力・出力のウェイトに制約を付ける領域限定法, 時系列変化を扱うためのウィンドー分析などが提案されている [4, 5].
[1] A. Charnes, W. W. Cooper and E. Rhodes, "Measuring Efficiency of Decision Making Units," European Journal of Operational Research, 2 (1978), 429-444.
[2] M. J. Farrell, "The Measurement of Productive Efficiency," Journal of the Royal Statistical Society, 120 (1957), 253-281.
[3] A. Charnes, W. W. Cooper, A. Y. Lewin and L. M. Seiford, Data Envelopment Analysis, Theory, Methodology and Applications, Kluwer Academic Publishers, 1994. 刀根薫, 上田徹 監訳, 『経営効率評価ハンドブック』, 朝倉書店, 2000.
[4] 刀根薫, 『経営効率性の測定と改善―包絡分析法DEAによる』, 日科技連, 1993.
[5] W. W. Cooper, L. M. Seiford and K. Tone, Data Envelopment Analysis, A Comprehensive Text with Models, Applications, References and DEA-Solver Software, Kluwer Academic Publishers, 1999.
N,N‐ジエチルアニリン
Dea
DEA
出典: フリー百科事典『ウィキペディア(Wikipedia)』 (2017/05/09 17:45 UTC 版)
DEA
- 麻薬取締局 (Drug Enforcement Administration)
- Data Encryption Standard (DES)に用いられているアルゴリズムを Data Encryption Algorithm と呼称することがある
- デラ・ガージ・カーン空港のIATAコード
- デジタルエンタテインメントアカデミー
- フランスにかつて存在した学位の一種。 diplôme d’études approfondiesのこと。
- フランスの救急に関わる専門職学位。DEA (学位)を参照。
 | このページは曖昧さ回避のためのページです。一つの語句が複数の意味・職能を有する場合の水先案内のために、異なる用法を一覧にしてあります。お探しの用語に一番近い記事を選んで下さい。このページへリンクしているページを見つけたら、リンクを適切な項目に張り替えて下さい。 |
DEA
出典: フリー百科事典『ウィキペディア(Wikipedia)』 (2021/05/19 06:02 UTC 版)
エノラ・コープランド アメリカ人女性。DEA捜査官。堀田の元妻である。堀田がメキシコに雲隠れしてから3年近く彼を探していた。ようやく居場所を掴むと堀田捜索を手伝った人物の姪である恵那の捜索を彼にまかせる傍ら、ゴールドスミス一家のMOディスクを抑えるべくレヴェル達とWN銀行にいた際、襲撃事件に巻き込まれ、そこで芹間に出会う。事件後は芹間の足取りを追うべく捜査主任として捜査を開始。クリスをブロウトン一味との銃撃戦を経て、辛くも保護したのち、芹間を見たというローゼンマンと部下のジムと共にメキシコへ。アルバレスファミリーの殺し屋、ディエゴと協力し、命令を違反してまでも芹間たちの足取りを追い続ける。コルト・オフィサーズモデルを所持。 グレアム・レヴェル アメリカ人男性。DEA捜査官。エノラの現在の夫である。エノラが未だに前の夫である堀田のことを気にかけるのを快く思っていない。実際、堀田の元に恵那の捜査資料を届けたが彼自身は堀田の復帰に乗り気でなく、メキシコで彼に辛辣な言葉を投げかける。WN銀行襲撃後は本部で待機していたが、命令違反を犯しメキシコに残り続けるエノラに業を煮やした上司からメキシコに行くように命令を受ける。SIG SAUER P229を所持。 ジム アメリカ人男性。DEA捜査官でエノラの部下。サングラスをかけており、素顔は分からない。芹間の追跡のためにエノラ、ローゼンマンと共にメキシコへ入る。が、捜査の途中にエノラが恵那と知り合いだということを知ったローゼンマンによって証拠隠滅のために殺害されてしまう。殺害直前にローゼンマンの謀略に気がついたがエノラに知らせるには至らなかった。 アラン アメリカ人男性。DEA捜査官でエノラの部下。クリス保護の際にブロウトン一家の殺し屋と交戦した際に負傷。メキシコには行かず、本部で待機。連絡係として働く。
※この「DEA」の解説は、「ワイルダネス」の解説の一部です。
「DEA」を含む「ワイルダネス」の記事については、「ワイルダネス」の概要を参照ください。
「dea」の例文・使い方・用例・文例
- deaのページへのリンク



