極座標
極座標
出典: フリー百科事典『ウィキペディア（Wikipedia）』 (2021/07/06 14:23 UTC 版)
「ベルトラン・ダルブーの定理」の記事における「極座標」の解説
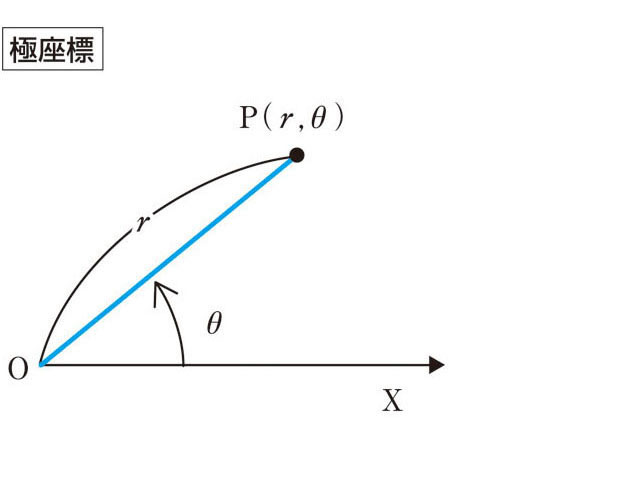
極座標 ( r , θ ) {\displaystyle (r,\theta )} は x = r cos θ {\displaystyle x=r\cos \theta } , y = r sin θ {\displaystyle y=r\sin \theta } により定義され、次の形のハミルトニアン H = 1 2 ( p r 2 + p θ 2 r 2 ) + U 1 ( r ) + U 2 ( θ ) r 2 {\displaystyle H={\frac {1}{2}}\left(p_{r}^{2}+{\frac {p_{\theta }^{2}}{r^{2}}}\right)+U_{1}(r)+{\frac {U_{2}(\theta )}{r^{2}}}} の場合に変数分離可能となる。独立な積分は Φ = 1 2 p θ 2 + U 2 ( θ ) {\displaystyle \Phi ={\frac {1}{2}}p_{\theta }^{2}+U_{2}(\theta )} である。
※この「極座標」の解説は、「ベルトラン・ダルブーの定理」の解説の一部です。
「極座標」を含む「ベルトラン・ダルブーの定理」の記事については、「ベルトラン・ダルブーの定理」の概要を参照ください。
ウィキペディア小見出し辞書の「極座標」の項目はプログラムで機械的に意味や本文を生成しているため、不適切な項目が含まれていることもあります。ご了承くださいませ。
お問い合わせ。
「極座標」の例文・使い方・用例・文例
極座標と同じ種類の言葉
- 極座標のページへのリンク
