Описане коло

Описане коло многокутника — коло, що містить всі вершини многокутника. Центром є точка (прийнято позначати O) перетину серединних перпендикулярів до сторін многокутника.
Центр описаного кола опуклого n-кутника лежить на точці перетину серединних перпендикулярів його сторін. Звідси випливає, що коли навколо n-кутника побудоване описане коло, то всі серединні перпендикуляри до його сторін перетинаються в одній точці (центрі кола).
Навколо будь-якого правильного многокутника можна описати коло.

- Навколо будь-якого трикутника можна описати коло, до того ж тільки одне. Його центром буде точка перетину серединних перпендикулярів.
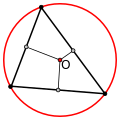
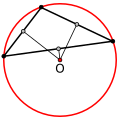
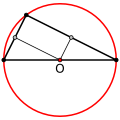
- У гострокутного трикутника центр описаного кола лежить всередині, у тупокутного — поза трикутником, у прямокутного — на середині гіпотенузи.
-
Гострокутний
-
Тупокутний
-
Прямокутний
Позначаємо літерою О точку перетину серединних перпендикулярів до його сторін та проведемо відрізки ОА, ОВ і ОС. Оскільки точка О рівновіддалена від вершин трикутника АВС, то ОА = OB = ОС. Тому коло з центром О радіусу ОА проходить через всі три вершини трикутника і, отже, є описаним навколо трикутника ABC.
- 3 4 кіл, описаних відносно серединних трикутників (утворених середніми лініями трикутника), перетинаються в одній точці всередині трикутника. Ця точка і є центром описаного кола основного трикутника.
- Центр описаного навколо трикутника кола служить ортоцентром трикутника з вершинами на серединах сторін даного трикутника. Ортоцентр трикутника — це точка перетину висот трикутника або їх продовжень.
- Відстань від вершини трикутника до ортоцентра вдвічі більше, ніж відстань від центра описаного кола до протилежної сторони.
- Радіус описаного кола можна знайти за формулами:
- Де:
- — сторони трикутника,
- — кут, що лежить навпроти сторони ,
- — півпериметр трикутника.
- — площа трикутника.
- — сторони трикутника,
- Положення центра описаного кола.
Нехай радіус-вектори вершин трикутника, — радіус-вектор центра описаного кола. Тоді
де
- Рівняння описаного кола.
Нехай координати вершин трикутника в певній декартовій системі координат на площині, — координати центра описаного кола. Тоді
а рівняння описаного кола має вигляд
Для точок , що лежать всередині кола, визначник негативний, а для точок поза нею — позитивний.
- Теорема про тризубець: Якщо — точка перетину бісектриси кута з описаним колом, а — центр вписаного кола то .
- Формула Ейлера: Якщо — відстань між центрами вписаного і описаного кіл, а їхні радіуси дорівнюють і відповідно, то .


Вписаний простий (без самоперетинів) чотирикутник обов'язково є опуклим .
Навколо опуклого чотирикутника можна описати коло тоді й тільки тоді, коли сума його внутрішніх протилежних кутів дорівнює 180 ° (π радіан).
Радіус описаного кола правильного -кутника з довжиною сторін дорівнює:
Можна описати коло навколо:
- будь-якого прямокутника (окремий випадок: квадрат)
- будь-якої рівнобедреної трапеції
- Теорема Птолемея: у чотирикутника, вписаного в коло, добуток довжин діагоналей дорівнює сумі добутків довжин пар протилежних сторін:[1]
- |AC|·|BD| = |AB|·|CD| + |BC|·|AD|
Якщо з відрізків скласти многокутник, то його площа буде максимальною, коли він вписаний.
- Понарин Я. П. Элементарная геометрия. В 2 тт. — М.: МЦНМО, 2004. — С. 53-54. — ISBN 5-94057-170-0
- Л. Е. Гендельштейн, А. П. Єршова, Наочний довідник з геометрії, Гімназія, 1997 — ISBN 966-562-080-0.