Dik üçgen
| Geometri |
|---|
 |
| Geometriciler |
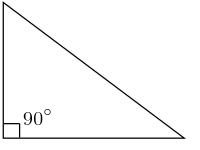
Dik üçgen, iç açılarından biri 90° olan üçgendir. Çemberde çapı gören çevre açı 90°'dir.
İlgili bağıntılar
[değiştir | kaynağı değiştir]Pisagor teoremi
[değiştir | kaynağı değiştir]Pisagor teoremi, herhangi bir dik üçgende kenarlar arasındaki bağıntıya verilen addır. Bu bağıntıya göre, dik kenarların karelerinin toplamı, hipotenüsün karesine eşittir.
pisagor bağıntısında 90 derecenin karşısındaki kenara hipotenüs adı verilir. Hipotenüsün karesi diğer dik kenarların karesinin toplamına eşittir. İki dik kenarın kareleri toplanır, çıkan sonucun karekökü alınarak hipotenüsün uzunluğu bulunur.
Özel dik üçgenler
[değiştir | kaynağı değiştir]Açıya göre
[değiştir | kaynağı değiştir]
45-45-90 üçgeni
[değiştir | kaynağı değiştir]45-45-90 üçgeni bir ikizkenar dik üçgendir. Üçgenin dik kenarları birbirine eşit ve hipotenüsü dik kenarların katıdır. Oran aşağıdaki gibidir:
İspatı ise çok basittir. Bir dik kenara 1 cm denilirse, ikizkenarlıktan dolayı diğer dik kenar da 1 cm olmak zorundadır. Pisagor Teoremi'nden de hipotenüs çıkar.
30-60-90 üçgeni
[değiştir | kaynağı değiştir]
Açıları 30-60-90 olan bir dik üçgende hipotenüs, 30°'nin karşısındaki kenar ve 60°'nin karşısındaki kenar arasında sırasıyla aşağıdaki oran vardır:
30°'nin karşısındaki kenarın katıdır. İspatı ise eşkenar üçgen vasıtasıyla yapılır. Kenarları 2 cm olan bir eşkenar üçgende köşeden indirilen dikme kenarı iki eş parçaya bölecektir. Aynı zamanda da açıortay olacaktır. Kenarortay olduğu için oluşan dik üçgenin alt dik kenarı 1 cm olacaktır. Açıortay olduğu için de dik üçgenin bir açısı 30° olacaktır. Eşkenar üçgenin bir kenarı, oluşan dik üçgenin hipotenüsü olacağından yapılacak Pisagor bağıntısı ile de indirilen dikme cm bulunacaktır.
22,5-67,5-90 üçgeni
[değiştir | kaynağı değiştir]Bu üçgende ise 22,5°'lik açının karşısındaki dik kenar 1 cm ise, 67,5°'lik açının karşısındaki kenar cm olur. İspatı ise 67,5°'lik açıyı 45° ve 22,5° şeklinde parçalayarak yapılır. Bu şekilde altta oluşan ikizkenar dik üçgende alt dik kenar 1 cm olursa hipotenüs cm olur. Yukarıda oluşacak ikizkenar üçgende de parçalanan kenarın diğer üst tarafı hipotenüse eşit olur. Alt parçası da ikizkenar dik üçgenden dolayı 1 cm bulunacağından elde edilir. Ve yine kaynaklarda pek bahsedilmeyen ama soruların çözümünde kolaylık sağlayan bir özellik: 22,5-67,5-90 üçgeninde hipotenüs, dik köşeden hipotenüse indirilen dikmenin 2 katı olur.
15-75-90 üçgeni
[değiştir | kaynağı değiştir]Bu üçgende 15°'lik açının karşısındaki kenar 1 cm ise 75°'lik kenarın karşısındaki kenar cm olur. İspatı ise 22,5-67,5-90 üçgenindeki gibidir. Tek farkı, 75°'lik açının 15° ve 60°'lik açılara bölünmesidir.
Ayrıca bu üçgende hipotenüse indirilen dikme, hipotenüsün katıdır.
Kenarlara göre özel dik üçgenler genelde okullarda soru yazılırken işlem kolaylığı sağlamak amacıyla kullanılır. Bazı özel üçgenler şunlardır:
Bu üçgenlerin kenar uzunlukları aynı oranda artırılarak yine uygun dik üçgenler elde edilebilir (örneğin, 3-4-5 ve 6-8-10).
Ayrıca herhangi bir tek sayıyı (asal olmak şartı ile) kenar uzunluğu olarak belirlersek karesinin ardışık toplamları da diğer iki kenarı verecektir. Örnek olarak; 7=>7'nin karesi 49=25+24 7,25,24 şeklinde özel bir dik üçgen vardır. 9=>9'un karesi 81=40+41 9,40,41 şeklinde özel bir dik üçgen vardır. Ve dik üçgende kenarların tam sayı olduğu koşulda, en kısa kenarı tek sayı ise kalan kenarların bu kurala uyması şarttır.