For the sake of having fun1
I wrote a piece of cumbersome code.
\numberrange{⟨amount of digits of 2nd number that shall at least be printed⟩}%
{⟨1st number⟩}%
{⟨2nd number⟩}
The main loop of the routine is \UD@numberrangeloop.
The main loop \UD@numberrangeloop processes arguments according to the following pattern:
\UD@numberrangeloop{⟨least significant digit of 1st number not processed yet⟩}%
⟨remaining digits of 1st number in reversed order⟩\bizarre
{⟨least significant digit of 2nd number not processed yet⟩}%
⟨remaining digits of 2nd number in reversed order⟩\bizarre
{⟨2nd number, all digits in correct order⟩}%
{⟨amount of m corresponding to difference of amount of digits of 2nd number that shall at least be printed and digits gathered so far⟩}%
{⟨to-be printed digits of 2nd number gathered so far⟩}%
{⟨digits of 2nd number that need to be added to ⟨digits of 2nd number gathered so far⟩ if another pair of differing digits is found⟩}%
{⟨\@firstoftwo\@secondofto/\@secondoftwo\@firstoftwo - "flag" denoting whether collecting different digits or collecting equal digits⟩}%
\UD@numberrangeloop is a loop which compares digits of the 1st number with digits of the 2nd number, beginning with the least significant digits of these numbers, ending with the most significant digits of these numbers:
As long as different digits are encountered, the 2nd number's digits are prepended to the ⟨to-be printed digits of 2nd number gathered so far⟩.
If equal digits are encountered, the loop switches to prepending equal digits to ⟨digits of 2nd number that need to be added to ⟨to-be printed digits of 2nd number gathered so far⟩ if another pair of differing digits is found⟩.
As long as equal digits are encountered, the 2nd number's digits are prepended to ⟨digits of 2nd number that need to be added to ⟨to-be printed digits of 2nd number gathered so far⟩ if another pair of differing digits is found⟩.
If different digits are encountered again, ⟨digits of 2nd number that need to be added to ⟨to-be printed digits of 2nd number gathered so far⟩ if another pair of differing digits is found⟩ is prepended to the ⟨to-be printed digits of 2nd number gathered so far⟩ and the loop switches to collecting different digits.
The loop ends when all digits of one of the numbers forming the range are processed.
If hereby it turns out that the digit sequences of the two numbers are of different length, then ⟨2nd number, all digits in correct order⟩ is delivered.
If hereby it turns out that the digit sequence of the 2nd number is shorter than the digit sequence of the 1st number, leading zeros are added to the ⟨digits of 2nd number gathered so far⟩ for ensuring equal length of both digit-sequences.
Otherwise you could not distinhuish
1002--5 in the sense of "from 1002 to 1005"
fom
1002--5 in the sense of "from 1002 downto 5"
But you can: In the further case you get:
1002--5 in the sense of "from 1002 to 1005"
In the latter case you get:
1002--0005 in the sense of "from 1002 downto 5"
A minus-sign at the left of the first number denotes that both numbers are negative. In this case digits of the 2nd number are elided.
A minus-sign at the left of the first number and a plus-sign at the right number denotes that the 1st number is negative while the 2nd number is positive. In this case no digits are elided.
A minus-sign only at the right number denotes that the 1st number is positive while the 2nd number is negative. In this case no digits are elided.
If both the ⟨1st number⟩ and the ⟨2nd number⟩ have less digits than denoted by
⟨amount of digits of 2nd number that shall at least be printed⟩, then
⟨amount of digits of 2nd number that shall at least be printed⟩ is not obeyed and with both numbers all digits are printed. If the digit sequence of the 2nd number is shorter than the digit sequence of the 1st number, leading zeros are added to the 2nd number for ensuring equal length of both digit-sequences.
\errorcontextlines=10000
\makeatletter
\@ifdefinable\UD@stopromannumeral{\chardef\UD@stopromannumeral=`\^^00}%
\newcommand\UD@PassFirstToSecond[2]{#2{#1}}%
\newcommand\UD@Exchange[2]{#2#1}%
\newcommand\UD@plus{\ifvmode\leavevmode\fi\lower-.2\ht\strutbox\hbox{$\scriptscriptstyle(\kern-.15em+\kern-.15em)$}}
\newcommand\UD@minus{\ifvmode\leavevmode\fi\lower-.2\ht\strutbox\hbox{$\scriptscriptstyle(\kern-.15em-\kern-.15em)$}}
\newcommand\numberrange[3]{%
\romannumeral
\expandafter\UD@PassFirstToSecond\expandafter{\romannumeral\number\number#1 000}{%
\expandafter\UD@PassFirstToSecond\expandafter{\number#3}{%
\expandafter\UD@PassFirstToSecond\expandafter{\number#2}{%
\UD@Initializenumberrangeloop
}%
}%
}%
}%
\@ifdefinable\UD@reverseargloop{%
\long\def\UD@reverseargloop#1#2\bizarre#3{%
\ifcat$#2$\expandafter\@firstoftwo\else\expandafter\@secondoftwo\fi
{\UD@Exchange{#3{}{}\bizarre}}{\UD@reverseargloop#2\bizarre{#1#3}}%
}%
}%
\newcommand\UD@extractfirstcomponent[1]{%
\UD@@extractfirstcomponent#1{}\bizarre
}%
\@ifdefinable\UD@@extractfirstcomponent{%
\long\def\UD@@extractfirstcomponent#1#2\bizarre{#1}%
}%
\newcommand\UD@Initializenumberrangeloop[3]{%
\expandafter\UD@Exchange\expandafter{%
\romannumeral
\if-\UD@extractfirstcomponent{#1}\expandafter\@firstoftwo\else\expandafter\@secondoftwo\fi
{%
\if-\UD@extractfirstcomponent{#2}\expandafter\@firstoftwo\else\expandafter\@secondoftwo\fi
{%
\expandafter\UD@PassFirstToSecond\expandafter{\@firstoftwo{}#2}{%
\expandafter\UD@reverseargloop\@firstoftwo{}#2{}{}\bizarre{}{%
\expandafter\UD@reverseargloop\@firstoftwo{}#1{}{}\bizarre{}{%
\UD@numberrangeloop
}%
}%
}{#3}{}{}{\@secondoftwo\@firstoftwo}%
}{%
\ifnum#2=0 \expandafter\@firstoftwo\else\expandafter\@secondoftwo\fi
{%
\expandafter\UD@stopromannumeral\expandafter-\expandafter-\romannumeral
\expandafter\UD@leadingzeros\expandafter{\romannumeral\UD@reduce{#1}{-#2}}%
}{%
\UD@stopromannumeral--\UD@plus
}%
#2%
}%
}{%
\if-\UD@extractfirstcomponent{#2}\expandafter\@firstoftwo\else\expandafter\@secondoftwo\fi
{%
\@firstoftwo{\UD@stopromannumeral--\UD@minus}#2%
}{%
\UD@reverseargloop#2{}{}\bizarre{}{%
\UD@reverseargloop#1{}{}\bizarre{}{%
\UD@numberrangeloop
}%
}{#2}{#3}{}{}{\@secondoftwo\@firstoftwo}%
}%
}%
}{%
\if-\UD@extractfirstcomponent{#1}\expandafter\@firstoftwo\else\expandafter\@secondoftwo\fi
{%
\UD@stopromannumeral\@firstoftwo\UD@minus#1%
}{\UD@stopromannumeral#1}%
}%
}%
\newcommand\UD@leadingzeros[1]{%
\ifcat$#1$\expandafter\@firstoftwo\else\expandafter\@secondoftwo\fi
{\UD@stopromannumeral}%
{\expandafter\UD@leadingzeros\expandafter{\@firstoftwo{}#1}0}%
}%
\newcommand\UD@reduce[2]{%
\ifcat$#1$\expandafter\@firstoftwo\else\expandafter\@secondoftwo\fi
{\UD@stopromannumeral}{%
\ifcat$#2$\expandafter\@firstoftwo\else\expandafter\@secondoftwo\fi
{%
\UD@stopromannumeral#1%
}{%
\expandafter\UD@PassFirstToSecond\expandafter{\@firstoftwo{}#2}{%
\expandafter\UD@reduce\expandafter{\@firstoftwo{}#1}}%
}%
}%
}%
\@ifdefinable\UD@pumpup{%
\long\def\UD@pumpup#1#2#3#4\bizarre{%
\ifcat$#1$\expandafter\@firstoftwo\else\expandafter\@secondoftwo\fi
{\UD@stopromannumeral--#2}{%
\ifcat$#4$\expandafter\@firstoftwo\else\expandafter\@secondoftwo\fi
{\UD@stopromannumeral--#2}%
{\expandafter\UD@pumpup\expandafter{\@firstoftwo{}#1}{#3#2}#4\bizarre}%
}%
}%
}%
\@ifdefinable\UD@numberrangeloop{%
\long\def\UD@numberrangeloop#1#2\bizarre#3#4\bizarre#5#6#7#8#9{%
\ifcat$#2$\expandafter\@firstoftwo\else\expandafter\@secondoftwo\fi
{%
\ifcat$#4$\expandafter\@firstoftwo\else\expandafter\@secondoftwo\fi
{%
\ifcat$#7$\expandafter\@firstoftwo\else\expandafter\@secondoftwo\fi
{%
\UD@stopromannumeral
}{%
\UD@reverseargloop#8{}{}\bizarre{}{%
\expandafter\UD@stopromannumeral
\romannumeral
\UD@pumpup{#6}{#7}%
}%
}%
}{%
\UD@stopromannumeral
--#5%
}%
}{%
\ifcat$#4$\expandafter\@firstoftwo\else\expandafter\@secondoftwo\fi
{%
\expandafter\UD@stopromannumeral\expandafter-\expandafter-\romannumeral
\expandafter\UD@leadingzeros\expandafter{\@firstoftwo{}#2}#5%
}{%
\if#1#3\expandafter\@firstoftwo\else\expandafter\@secondoftwo\fi
#9%
{%
\@firstoftwo#9{%
\UD@numberrangeloop#1#2\bizarre#3#4\bizarre{#5}{#6}{#7}{}{\@secondoftwo\@firstoftwo}%
}{%
\expandafter\UD@PassFirstToSecond\expandafter{\romannumeral\UD@reduce{#6}{#8}}{%
\UD@numberrangeloop#1#2\bizarre#3#4\bizarre{#5}}{#8#7}{}{\@firstoftwo\@secondoftwo}%
}%
}{%
\@firstoftwo#9{%
\ifcat$#6$\expandafter\@firstoftwo\else\expandafter\@secondoftwo\fi
{\UD@PassFirstToSecond{}}%
{\expandafter\UD@PassFirstToSecond\expandafter{\@firstoftwo{}#6}}%
{\UD@numberrangeloop#2\bizarre#4\bizarre{#5}}{#3#7}{#8}{#9}%
}{%
\UD@numberrangeloop#2\bizarre#4\bizarre{#5}{#6}{#7}{#3#8}{#9}%
}%
}%
}%
}%
}%
}%
\makeatother
\documentclass{article}
\begin{document}
\begin{tabular}{@{} ll @{}}
Input & Output \\
\hline
\verb+\numberrange{1}{1}{1}+ & \numberrange{1}{1}{1} \\
\verb+\numberrange{1}{0}{0}+ & \numberrange{1}{0}{0} \\
\verb+\numberrange{1}{1}{12}+ & \numberrange{1}{1}{12} \\
\verb+\numberrange{1}{10}{20}+ & \numberrange{1}{10}{20} \\
\verb+\numberrange{0}{0}{-948}+ & \numberrange{0}{0}{-948} \\
\verb+\numberrange{0}{-948}{0}+ & \numberrange{0}{-948}{0} \\
\verb+\numberrange{0}{0}{948}+ & \numberrange{0}{0}{948} \\
\verb+\numberrange{0}{948}{0}+ & \numberrange{0}{948}{0} \\
\verb+\numberrange{20}{941}{48}+ & \numberrange{20}{941}{48} \\
\verb+\numberrange{20}{941}{8}+ & \numberrange{20}{941}{8} \\
\verb+\numberrange{0}{941}{48}+ & \numberrange{0}{941}{48} \\
\verb+\numberrange{0}{941}{8}+ & \numberrange{0}{941}{8} \\
\verb+\numberrange{0}{-941}{948}+ & \numberrange{0}{-941}{948} \\
\verb+\numberrange{0}{941}{-948}+ & \numberrange{0}{941}{-948} \\
\verb+\numberrange{0}{-941}{-948}+ & \numberrange{0}{-941}{-948} \\
\verb+\numberrange{0}{-948}{-941}+ & \numberrange{0}{-948}{-941} \\
\verb+\numberrange{0}{948}{941}+ & \numberrange{0}{948}{941} \\
\verb+\numberrange{0}{941}{948}+ & \numberrange{0}{941}{948} \\
\verb+\numberrange{1}{941}{948}+ & \numberrange{1}{941}{948} \\
\verb+\numberrange{2}{941}{948}+ & \numberrange{2}{941}{948} \\
\verb+\numberrange{3}{941}{948}+ & \numberrange{3}{941}{948} \\
\verb+\numberrange{4}{941}{948}+ & \numberrange{4}{941}{948} \\
\verb+\numberrange{1}{941}{959}+ & \numberrange{1}{941}{959} \\
\verb+\numberrange{1}{1001}{1007}+ & \numberrange{1}{1001}{1007} \\
\verb+\numberrange{1}{1001}{1021}+ & \numberrange{1}{1001}{1021} \\
\verb+\numberrange{1}{1001}{1201}+ & \numberrange{1}{1001}{1201} \\
\verb+\numberrange{1}{1001}{2001}+ & \numberrange{1}{1001}{2001} \\
\verb+\numberrange{1}{10}{5}+ & \numberrange{1}{10}{5} \\
\verb+\numberrange{1}{100}{99}+ & \numberrange{1}{100}{99} \\
\verb+\numberrange{1}{-10}{-15}+ & \numberrange{1}{-10}{-15} \\
\verb+\numberrange{1}{-10}{-5}+ & \numberrange{1}{-10}{-5} \\
\verb+\numberrange{1}{-10}{5}+ & \numberrange{1}{-10}{5} \\
\verb+\numberrange{1}{10}{-5}+ & \numberrange{1}{10}{-5} \\
\verb+\numberrange{1}{-100}{-99}+ & \numberrange{1}{-100}{-99} \\
\verb+\numberrange{1}{100100100}{200100100}+ & \numberrange{1}{100100100}{200100100} \\
\verb+\numberrange{1}{234100234}{123100123}+ & \numberrange{1}{234100234}{123100123} \\
\verb+\numberrange{1}{200100100}{200100100}+ & \numberrange{1}{200100100}{200100100} \\
\verb+\numberrange{1}{-200100100}{-200100100}+ & \numberrange{1}{-200100100}{-200100100} \\
\end{tabular}
\end{document}

1I say "for the sake of having fun" because—let's face it—compared to all the other solutions my piece of code is so long and confusing that it's not really reasonable for anyone to use it in their daily lives. I wrote it more out of defiant stubbornness: The other solutions consider the higher-order digits first. I wanted, to see the full spectrum of possibilities explored, a solution where the lower-order digits are considered first. ;-)

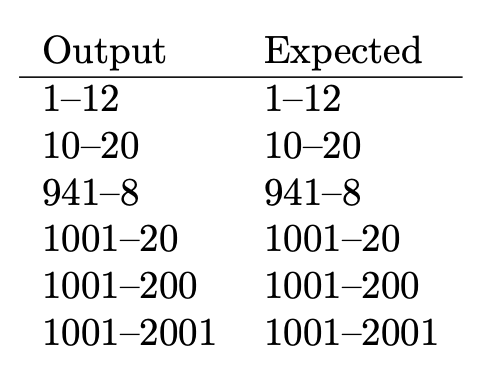


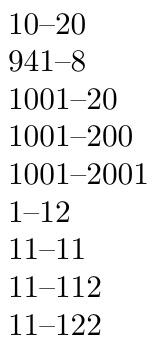

\numberrange{-1029}{-1020}?