Nice scientific pictures show off

Question

Task

Show off your best scientific illustration !

The main purpose of this question is to share beautiful scientific pictures, preferably with an educational aspect.

---

Content

Your post must contain a nice picture and the associated code. One can post several pictures, but it must be done in different replies. Of course, it must be done with LaTeX & Friends : the post must start with a short sentence to present the language that you chose (TikZ, Asymptote ...) and the main packages that helped you to make the picture. Don't hesitate to add comments.

---

Reward

The satisfaction to share without expecting a reward :)

Ok ... 300 points reputation bounty for the best up-voted post until the 15th of Feb.

---

Related links

I'll contact Texample.net webmaster to see if he is interested to share the best illustrations, with the participant's agreement of course.

Contest: Show Off Your Skillz in TeX & Friends

Answer 1

The following image illustrates the blowup of a plane at a point--an important construction in algebraic geometry (compare the cover of this book). The image was produced using Asymptote. (Note: the code and the image have both been refined since they were first posted.)

The vector image may be viewed by following this link.

settings.outformat="pdf";
settings.render=0;
settings.prc=false;

usepackage("lmodern");
usepackage("fontenc","T1");
usepackage("amssymb");  // for the \mathbb command
defaultpen(fontsize(10pt));

import graph3;
size(400,400);
currentprojection=orthographic(5,-10,4);

real R=8;

struct scaler {
    private real factor;

    void operator init(real factor) {
        this.factor = factor;
    }

    real scale(real t) {return factor*atan(tan(t)/factor);}
    real invert(real t) {return tan(atan(t)*factor)/factor;}
}

scaler theScaler = scaler(6);

triple f(pair t) {
    real r = t.x;
    real theta = 2 * atan(t.y*2/pi);
//  real theta = -t.y;
    return (r*cos(theta),r*sin(theta),theScaler.scale(theta));
}

int resolution = 10;
real epsilon = .01;
real vmin = -pi/2;
real vmax = pi/2;
real umin = -R;
real umax = R;
splinetype[] Linear = new splinetype[] {linear, linear, linear};
splinetype[] ZMonotonic = new splinetype[] {notaknot, notaknot, monotonic};
surface sBack=surface(f,(umin,vmin),(0,vmax),nu=resolution, nv=2*resolution,  usplinetype=Linear, vsplinetype = ZMonotonic);
surface sFront = surface(f, (0,vmin), (umax,vmax), nu=resolution, nv=2*resolution, usplinetype=Linear, vsplinetype=ZMonotonic);

pen meshpen = heavygray + linewidth(0.2);

material surfacepen = 
    material(diffusepen=lightgray+opacity(0.5), 
        emissivepen=gray(0.3),
        specularpen=gray(0.2));

draw(sBack, surfacepen=surfacepen, meshpen=meshpen);
draw(f((0,vmin)) -- f((0,vmax)), darkgray+linewidth(1.0));   // the exceptional divisor
draw(sFront, surfacepen=surfacepen, meshpen=meshpen);


pen planePen = black+linewidth(0.3);

triple bottomPoint = f((0,vmin));
triple planeCenter = 2.0*bottomPoint;
draw((bottomPoint-.6Z)--(planeCenter+.6Z), arrow=Arrow3(TeXHead2), p=linewidth(0.9),
     L="$\pi_1$");

real planeZ = planeCenter.z;

triple h(pair t) {
    return (t.x, t.y, planeZ);
}

triple g(pair t) {
    triple projectFrom = f(t);
    return h((projectFrom.x, projectFrom.y));
}
triple g(real tx, real ty) { return g((tx, ty)); }

real planeRadius = R+1;
surface thePlane = surface(h, (-planeRadius,-planeRadius),(planeRadius,planeRadius),
    nu=1);

path3 planeOutline = h((-planeRadius,-planeRadius)) -- h((-planeRadius,planeRadius)) -- h((planeRadius,planeRadius)) -- h((planeRadius,-planeRadius)) -- cycle;

for (real u = 0; u <= R; u += R/resolution)
  draw(circle(planeCenter, u), planePen);
for (real v = vmin; v < vmax; v += (vmax-vmin)/(2*resolution)) {
  draw(g(umin,v) -- g(umax,v), planePen);
}
draw(planeOutline, p=planePen);

//Embed the label "\mathbb P^2" on the plane:
real labelScale = 1.5;  
Label planeLabel = Label(scale(labelScale, labelScale*1.3, 1)*"$\mathbb P^2$", fontsize(10pt));
Label placedPlaneLabel = shift((planeRadius-1.2),(planeRadius-1.5),planeCenter.z)*planeLabel;

label(planeLabel, position = (planeRadius-1.2, planeRadius-1.5, planeCenter.z));

Answer 2

Electric field due to 3 charges. The black one is a negative charge orbiting the other two positive charges.

\documentclass[pstricks,border=12pt]{standalone}
\usepackage{pst-electricfield}

\begin{document}
\multido{\i=0+15}{24}{%
\begin{pspicture*}(-4,-4)(4,4)
    \psElectricfield[Q={[-1 3 \i\space PtoC][1 1 1][1 -1 -1]},linecolor=red]
\end{pspicture*}}
\end{document}

Answer 3

One that I'm most proud of is a three-dimensional illustration of a signpost with various loads applied, shown here. I used the TikZ package. Commercial fonts have been removed in the code I've posted below. Looking back at the code, I probably could have written it a bit more efficiently (styles for face shading, more relative positioning, etc.), but c'est la vie.

\documentclass{standalone}
\usepackage{tikz}

% Vector Styles
\tikzset{
  load/.style   = {ultra thick,-latex},
  stress/.style = {-latex},
  dim/.style    = {latex-latex},
  axis/.style   = {-latex,black!55},
}

% Drawing View
\tikzset{dimetric2/.style={
  x={(0.935cm,-0.118cm)},
  y={(0.354cm, 0.312cm)},
  z={(0.000cm, 0.943cm)},
}}

\begin{document}
  \begin{tikzpicture}
    \node (origin) at (0,0) {}; % shift relative baseline
    \coordinate (O) at (2,3);
    \draw[fill=gray!10] (O) circle (1);
    \draw[fill=white] (O) circle (0.75) node[below,yshift=-1.125cm] {Signpost Cross Section};
    \draw[dim] (O) ++(-0.75,0) -- ++(1.5,0) node[midway,above] {$d_i$};
    \draw[dim] (O) ++(-1,1.25) -- ++(2,0) node[midway,above] {$d_o$}; 
    \foreach \x in {-1,1} {
      \draw (O) ++(\x,0.25) -- ++(0,1.25);
    }
  \end{tikzpicture}
  \begin{tikzpicture}[dimetric2]
        \coordinate (O) at (0,0,0);
        \draw[axis] (O) -- ++(6,0,0) node[right] {$x$};
        \draw[axis] (O) -- ++(0,6,0) node[above right] {$y$};
        \draw[axis] (O) -- ++(0,0,6) node[above] {$z$};
        \draw[fill=gray!50] (0,0,-0.5) circle (0.5); 
        \fill[fill=gray!50] (-0.46,-0.2,-0.5) -- (0.46,0.2,-0.5) -- (0.46,0.2,0) -- (-0.46,-0.2,0) -- cycle;
        \draw[fill=gray!20] (O) circle (0.5);
    \draw (0.46,0.2,-0.5) -- ++(0,0,0.5) node[below right,pos=0.0] {Fixed Support};
    \draw (-0.46,-0.2,-0.5) -- ++(0,0,0.5);
    \draw[fill=gray!10] (O) circle (0.2);
    \fill[fill=gray!10] (-0.175,-0.1,0) -- (0.175,0.1,0) -- ++(0,0,4) -- (-0.175,-0.1,4) -- cycle;
    \draw (-0.175,-0.1,0) -- ++(0,0,4);
    \draw (0.175,0.1,0) -- ++(0,0,4) node[right,midway] {Steel Post};
    \draw (4,0,3.95) -- ++(0,0,-1);
    \foreach \z in {0.5,0.75,...,5} {
      \draw[-latex] (-2*\z/5-0.2,0,\z) -- (-0.2,0,\z);
    }
    \draw[load] (0,0,4) -- ++(0,0,-1.25) node[right,xshift=0.1cm] {$F_{z1}$};
    \draw[fill=gray!20] (-0.25,-0.25,5) -- (4,-0.25,5) -- (4,+0.25,5) -- (-0.25,+0.25,5) -- cycle; 
    \draw[fill=gray!50] (+4.00,-0.25,4) -- (4,+0.25,4) -- (4,+0.25,5) -- (+4.00,-0.25,5) -- cycle; 
    \draw[fill=gray!10] (-0.25,-0.25,4) -- (4,-0.25,4) -- (4,-0.25,5) -- (-0.25,-0.25,5) -- cycle; 
    \draw (4.05,0,4) -- ++(1,0,0);
    \draw (4.05,0,5) -- ++(1,0,0);
    \draw[dim] (4.5,0,0) -- ++(0,0,4) node[midway,right] {$h_1$};
    \draw[dim] (4.5,0,4) -- ++(0,0,1) node[midway,right] {$h_2$};
    \draw[dim] (0,0,3.4) -- ++(4,0,0) node[midway,below] {$b_2$};
    \coordinate (P) at (2,-0.25,4.5);
    \draw (P) -- ++(0,0,0.25);
    \draw (P) -- ++(0.25,0,0);
    \draw[dim] (2.125,-0.25,4.5) -- ++(0,0,-0.5) node[midway,right] {$z_1$};
    \draw[dim] (2,-0.25,4.625) -- ++(-2,0,0) node[midway,below] {$x_1$};
    \draw[load] (2,-2.45,4.5) -- ++(0,2.2,0) node[pos=0.0,right,xshift=0.08cm] {$F_{y1}$};
    \draw[axis,dashed,-] (O) -- (0,0,5);
    \draw (0,0,5.5) -- ++(4,0,0) node[midway,above] {$w_{z}$};
    \foreach \x in {0,0.25,...,4} {
      \draw[-latex] (\x,0,5.5) -- ++(0,0,-0.5);
    }
    \draw (-0.2,0,0) -- ++(-2,0,5) node[above,xshift=0.5cm] {$w_{x}=\frac{z}{h_1+h_2} w_0$};
  \end{tikzpicture}
\end{document}

Answer 4

\documentclass[border=0pt,pstricks]{standalone}
\usepackage{pst-coil,pstricks-add}
\usepackage[nomessages]{fp}

\FPset\CoilArm{0.25}
\FPset\CoilWidth{0.3}
\FPeval\CoilTurn{round(50/3:3)}
\FPeval\DeltaY{0.5}
\FPeval\Amp{1.5}
\FPeval\FPS{25}
\FPeval\Vx{2}% propagation speed
\FPeval\Period{1}% second

\psset
{
    coilarm=\CoilArm,
    coilwidth=\CoilWidth,
}


\newcommand\System[4][0]{% #1: frame, #2: x, #3: y, #4: label
    \uput[90](#2,4.25){#4}
    \FPeval\CoilHeight{round((4-(#3)-2*CoilArm)/(CoilWidth*CoilTurn):3)}
    \pszigzag[coilheight=\CoilHeight,linejoin=2](#2,4)(#2,#3)
    \ifnum#1=1
        \bgroup
            \psset{origin={#2,#3}}
            \psframe[dimen=inner,fillstyle=solid,fillcolor=black](-0.5,0)(0.5,-1)
            \psdot[linecolor=yellow](0,-0.5)
        \egroup
    \fi
}

\begin{document}
\FPeval\DeltaTime{round(1/\FPS:2)}
\FPeval\TotalFrame{round(\FPS*\Period:0)}
\multido{\n=0.00+\DeltaTime}{\TotalFrame}{%
\begin{pspicture*}[showgrid=false](-1.5,-2)(3.5,5)
    % Ceiling
    \psframe
    [
        fillstyle=vlines,
        hatchsep=2pt,
        hatchwidth=0.5\pslinewidth,
        hatchcolor=gray,
        hatchangle=45,
        %linestyle=none
    ](0,4)(2,4.25)
    % Spring without box
    \FPeval\Y{round(-DeltaY-Amp*cos(2*pi*\n/Period)+2:3)}
    \System[1]{1}{\Y}{A}
    \psplot[algebraic,linecolor=red,plotpoints=1000]
        {-1.5}{3.5}{-\DeltaY-\Amp*cos((2*\psPi/\Period)*((-\Vx*\n+x-1)/\Vx))+2-0.5}
\end{pspicture*}}

\end{document}

Answer 5

One of my favorites; this one's not so involved but I enjoy the simplicity of the code and the quality of the result. It uses pgfplots to display streamline data for vortex shedding from a square block at Re=100. The streamline data were computed by a Fortran code I wrote to model the flow.

The code:

\documentclass{standalone}
\usepackage{pgfplots}    % plot stuff
\pgfplotsset{compat=1.6} % avoid warnings

\begin{document}
\begin{tikzpicture}
\begin{axis}[
  axis equal image,
  xmin=13,xmax=35,
  ymin=0,ymax=3,
  width=7in,
  xlabel={$x/D$ (-)},
  ylabel={$y/D$ (-)},
]
  \foreach \num in {1,2,...,18} {
    \addplot[black] file {time43.39stream\num.dat};                          
  }
  \draw[fill=black] (axis cs:15,1) rectangle (axis cs:16,2);
\end{axis}
\end{tikzpicture}
\end{document}

The data files are quite large; they are available here for anyone wishing to reproduce my result. The full paper is available for download here. It includes many similar figures showing different times during the vortex shedding process.

Answer 6

Plan B as per tohecz: I'm a security engineer at Facebook and this is my fault.

Properties of water and steam (IAPWS-SF95 formulation), enthalpy-entropy diagram, actually used by our students (and colleagues, from time to time).

Compiled with lualatex for memory reasons. I'll not post the code here, as it is quite a lot and wouldn't work on other computers anyway. That, of course, has a reason: The IAPWS-SF95 is not really easy to handle, so I wrote programs in C++ that output tables for the properties at a certain pressure, temperature, etc. This might have been possible with luatex, but I'm not really experienced in lua. I've added the tex code below.

The latex code reads in a table of iso lines that must be generated first, then calls the external binaries with appropriate command line arguments and reads back the resulting iso line tables. That takes about 45 minutes on a decent desktop PC, so I added an option not to regenerate all the data. Cosmetic runs now take only a few minutes.

Overview:

A close-up near the critical point:

You can see that some lines with constant steam quality (x) are cut off near the critical point, otherwise they would be to close to each other.

Some labels:

Extra labels or extended labels as you can see them above are also specified in the table that is read in first. Major and minor iso lines have different strength. The grid is quiet, gray. All glyphs have some white padding around them. I don't like the white spots appearing near the intersections of some lines, I haven't yet mastered that art (they are also present in the printed diagram, but not as prominent as on screen).

The layout is for A2 paper, I'm thinking about making an A0 version that starts at lower enthalpy/entropy. It would have a large empty area at the lower right that I'd fill with some table for looking up exact values.

Holding the real printed diagram in my hands with a real gray grid was really great. An older version of this diagram existed at our institute before, but we ran out of prints and it contained some wrong values. That was my motivation to create this one.

Thanks to tex sx - many of the tikz/pgfplots/pgfplotstable tricks I used in this diagram are actually yours!

EDIT: OK, as so many others have also posted their code I thought I'd just post mine as well, but without the C++ part.

mollier.tex (main file):

%\listfiles
\documentclass{article}
\usepackage[a2paper,landscape,margin=0.9cm]{geometry}

\usepackage[latin1]{luainputenc}
\usepackage[T1]{fontenc}

\usepackage{sfmath}
\usepackage{icomma} % german decimal separator in math mode

\usepackage[ngerman]{babel}
\usepackage[locale=DE]{siunitx}

\usepackage[outline]{contour}
\contourlength{0.5pt}
\usepackage{color}

\usepackage{tikz,pgfplots,pgfplotstable}
\usetikzlibrary{intersections,calc}
% \pgfplotsset{compat=1.5}

\usepackage{etoolbox}
% \usepackage{hyperref}


% plotted entropy range
\edef\smin{4000}
\edef\smax{9200}
\pgfmathsetmacro{\dsa}{500} % major tick size
\pgfmathsetmacro{\dsb}{100} % intermediate tick size
\pgfmathsetmacro{\dsc}{10} % minor tick size

% plotted enthalpy range
\edef\hmin{2000}
\edef\hmax{3900}
\pgfmathsetmacro{\dha}{500} % major tick size
\pgfmathsetmacro{\dhl}{100} % label ticks size
\pgfmathsetmacro{\dhb}{50} % intermediate tick size
\pgfmathsetmacro{\dhc}{5} % minor tick size

% min, critical, max pressure, critical temperature
\edef\pmin{700}
\edef\pCrit{22064000}
\edef\pmax{10000e5}
\edef\tCrit{373.946}

% default number of points per plotted line
\edef\nSamples{500}

\input{createTicks}

\tikzset{minor grid style/.style={ultra thin,color=black!50}}
\tikzset{intermediate grid style/.style={thin,color=black!50}}
\tikzset{major grid style/.style={thin,color=black!50}}
\tikzset{hidden plot/.style={draw=none}}

\pgfplotsset{minor p plot/.style={black,very thin}}
\pgfplotsset{major p plot/.style={black,semithick}}
\pgfplotsset{minor T plot/.style={smooth,magenta,very thin}}
\pgfplotsset{major T plot/.style={smooth,magenta,semithick}}
\pgfplotsset{minor x plot/.style={smooth,black,very thin}}
\pgfplotsset{major x plot/.style={smooth,black,semithick}}

\tikzset{p plot label/.style={inner sep=1pt,outer sep=0pt,above=1pt,anchor=base,sloped,font={\footnotesize}}}
\tikzset{t plot label/.style={inner sep=1pt,outer sep=0pt,above=1pt,anchor=base,sloped,font={\footnotesize}}}
\tikzset{x plot label/.style={inner sep=1pt,outer sep=0pt,above=1pt,anchor=base,sloped,font={\footnotesize}}}

\pgfplotstableset{input filter/.style={y expr=\thisrow{h}/1e3}}
\sisetup{detect-all=true,parse-numbers=false}
\pgfkeys{/pgf/number format/.cd,set thousands separator={},set decimal separator={,}}

\pgfplotsset{mollier axis/.style={
  xmin=\smin,xmax=\smax,width=52cm,
  ymin=\hmin,ymax=\hmax,height=38cm,
  scale only axis,
  major tick length={0pt},
  minor tick length={0pt},
  grid=none,
  xtick=\sLabelTicks,
  xticklabel={\pgfmathparse{\tick/1e3}\num{\pgfmathprintnumber{\pgfmathresult}}},
  ytick=\hLabelTicks,
  yticklabel={\pgfmathparse{\tick}\pgfmathprintnumber{\pgfmathresult}},
}}

\newbool{createPTables}
\newbool{createTTables}
\newbool{createXTables}
\setbool{createPTables}{false}
\setbool{createTTables}{false}
\setbool{createXTables}{false}

\begin{document}
  \thispagestyle{empty}
  \input{createTables}
  \noindent\centering
\begin{tikzpicture}
    \begin{axis}[mollier axis,
                axis x line*=top,
                axis y line*=right,
                ]
    \end{axis}
    \begin{axis}[mollier axis,
                xlabel={\textsf{spezifische Entropie $s$ in \si[per-mode=fraction]{\kilo\joule\per\kilogram\per\kelvin}}},
                ylabel={\textsf{spezifische Enthalpie $h$ in \si[per-mode=fraction]{\kilo\joule\per\kilogram}}},
                ]
      \input{drawGrid}
      % plots
      % plots are drawn using external data files created by createTables.tex
      % the data files don't need to be recreated in each run.
      \input{plotp}
      \input{plotT}
      \input{plotx}
      % labels
      % labels are placed by creating a path between 2 points on a plot (using intersections)
      % and then adding a node between these points.
      \input{placePLabels}
      \input{placeTLabels}
      \input{placeXLabels}
      % mark critical point
      % the critical point is at the end of the x=1 plot (or x=0)
      \filldraw (coord-x1000m-end) circle(2pt) node[
        p plot label,right=2pt,font={\sffamily\footnotesize}
      ] {\contour{white}{K.P.}};
      % title/info box
      \draw (rel axis cs:1,0) node[
        draw=black,fill=white,above left=1em,align=left,font={\sffamily\footnotesize}
      ] {
        \begin{minipage}{7.3cm}
          \includegraphics[width=\textwidth,keepaspectratio]{Logo_mit_TUHH_deu_weiss.pdf}\\[1\baselineskip]
          \Huge Mollier $h$,$s$-Diagramm\\[2pt]
          \LARGE für Wasser, nach IAPWS-95 [1]\\[0.5\baselineskip]
          \large Christoph Redecker\\
          Institut für Thermofluiddynamik\\
          TU Hamburg-Harburg
        \end{minipage}
      };
      % frame
      \draw[major grid style] (axis cs:\smin,\hmin) rectangle (axis cs: \smax,\hmax);
    \end{axis}
    % IAPWS reference
    \draw (current axis.below south east) node[outer sep=0pt,inner sep=0pt,left] {
      \footnotesize\sffamily
      \begin{minipage}{12.2cm}
        \begin{itemize}
          \item[{[1]}] IAPWS, \textit{Revised Release on the IAPWS Formulation 1995 for the Thermodynamic Properties of Ordinary Water Substance for General and Scientific Use} (2009).
          \texttt{http://www.iapws.org}.
        \end{itemize}
      \end{minipage}
    };
    \draw (current axis.below south west) node[outer sep=0pt,inner sep=0pt,right] {
      \footnotesize\sffamily v 1.2, 23.\,10.\,2012
    };
  \end{tikzpicture}
\end{document}

createTicks.tex:

\gdef\sMajorTicks{}
{
  \pgfmathsetmacro{\ticks}{floor((\smax - \smin)/\dsa)+1}
  \def\tickSep{}
  \foreach \n in {1,...,\ticks}%
  {
    \pgfmathsetmacro{\s}{\smin + (\n-1)*\dsa}%
    \xdef\sMajorTicks{\sMajorTicks\tickSep\s}
    \xdef\tickSep{, }
  }
}
\let\sLabelTicks\sMajorTicks

\gdef\sInterTicks{}
{
  \pgfmathsetmacro{\ticks}{floor((\smax - \smin)/\dsb)+1}
  \def\tickSep{}
  \foreach \n in {1,...,\ticks}%
  {
    \pgfmathsetmacro{\s}{\smin + (\n-1)*\dsb}%
    \xdef\sInterTicks{\sInterTicks\tickSep\s}
    \xdef\tickSep{, }
  }
}

\gdef\sMinorTicks{}
{
  \pgfmathsetmacro{\ticks}{floor((\smax - \smin)/\dsc)+1}
  \def\tickSep{}
  \foreach \n in {1,...,\ticks}%
  {
    \pgfmathsetmacro{\s}{\smin + (\n-1)*\dsc}%
    \xdef\sMinorTicks{\sMinorTicks\tickSep\s}
    \xdef\tickSep{, }
  }
}

\gdef\hMajorTicks{}
{
  \pgfmathsetmacro{\ticks}{floor((\hmax - \hmin)/\dha)+1}
  \def\tickSep{}
  \foreach \n in {1,...,\ticks}%
  {
    \pgfmathsetmacro{\h}{\hmin + (\n-1)*\dha}%
    \xdef\hMajorTicks{\hMajorTicks\tickSep\h}
    \xdef\tickSep{, }
  }
}

\gdef\hInterTicks{}
{
  \pgfmathsetmacro{\ticks}{floor((\hmax - \hmin)/\dhb)+1}
  \def\tickSep{}
  \foreach \n in {1,...,\ticks}%
  {
    \pgfmathsetmacro{\h}{\hmin + (\n-1)*\dhb}%
    \xdef\hInterTicks{\hInterTicks\tickSep\h}
    \xdef\tickSep{, }
  }
}

\gdef\hMinorTicks{}
{
  \pgfmathsetmacro{\ticks}{floor((\hmax - \hmin)/\dhc)+1}
  \def\tickSep{}
  \foreach \n in {1,...,\ticks}%
  {
    \pgfmathsetmacro{\h}{\hmin + (\n-1)*\dhc}%
    \xdef\hMinorTicks{\hMinorTicks\tickSep\h}
    \xdef\tickSep{, }
  }
}

\gdef\hLabelTicks{}
{
  \pgfmathsetmacro{\ticks}{floor((\hmax - \hmin)/\dhl)+1}
  \def\tickSep{}
  \foreach \n in {1,...,\ticks}%
  {
    \pgfmathsetmacro{\h}{\hmin + (\n-1)*\dhl}%
    \xdef\hLabelTicks{\hLabelTicks\tickSep\h}
    \xdef\tickSep{, }
  }
}

createTables.tex

\pgfplotstableset{create on use/pBar/.style={create col/expr={\thisrow{p}*1e-5}}}
\pgfplotstableset{create on use/pMPa/.style={create col/expr={\thisrow{p}*1e-6}}}
\pgfplotstableset{create on use/xVal/.style={create col/expr={\thisrow{x}*1e-3}}}
\pgfplotstableread[col sep=semicolon,
  columns/p/.style={string type},
  columns/style/.style={string type},
  columns/label/.style={string type},
  columns/cmdoptions/.style={string type}
]{pTable.tab}{\pTable}
\pgfplotstableread[col sep=semicolon,
  columns/t/.style={string type},
  columns/style/.style={string type},
  columns/label/.style={string type},
  columns/cmdoptions/.style={string type}
]{tTable.tab}{\tTable}
\pgfplotstableread[col sep=semicolon,
  columns/x/.style={string type},
  columns/style/.style={string type},
  columns/label/.style={string type},
  columns/cmdoptions/.style={string type}
]{xTable.tab}{\xTable}
%************************************************
\ifbool{createPTables}{%
  \pgfplotstablegetrowsof{\pTable}
  \foreach \i[evaluate=\i as \row using int(\i-1)] in {1,...,\pgfplotsretval}%
  {%
    \pgfplotstablegetelem{\row}{p}\of\pTable%
    \edef\p{\pgfplotsretval}%
    \pgfplotstablegetelem{\row}{cmdoptions}\of\pTable%
    \edef\cmdoptions{\pgfplotsretval}%
    \edef\shellcmd{../isobar/bin/Debug/isobar\space%
      --p=\p\space%
      --s=[\smin:\smax]\space%
      --h=[\hmin e3:\hmax e3]\space%
      % number of amples is set per plot in pTables.tab
      --snap\space%
      \cmdoptions\space%
      > ./data/p\p Pa.dat}%
    \immediate\write18{\shellcmd}%
  }%
}%
{} % end of \ifbool{createPTables}
%
%************************************************
\ifbool{createTTables}{%
  \pgfplotstablegetrowsof{\tTable}
  \foreach \i[evaluate=\i as \row using int(\i-1)] in {1,...,\pgfplotsretval}%
  {%
    \pgfplotstablegetelem{\row}{t}\of\tTable%
    \edef\t{\pgfplotsretval}%
    \pgfplotstablegetelem{\row}{cmdoptions}\of\tTable%
    \edef\cmdoptions{\pgfplotsretval}%
    \edef\shellcmd{../isotherm/bin/Debug/isotherm\space%
      --t=\t\space%
      --s=[\smin:\smax]\space%
      --h=[\hmin:\hmax]\space%
      --snap\space%
      \cmdoptions\space%
      > ./data/t\t C.dat}%
    \immediate\write18{\shellcmd}%
  }%
}%
{} % end of \ifbool{createTTables}
%
%************************************************
\ifbool{createXTables}{%
  \pgfplotstablegetrowsof{\xTable}
  \foreach \i[evaluate=\i as \row using int(\i-1)] in {1,...,\pgfplotsretval}%
  {%
    \pgfplotstablegetelem{\row}{x}\of\xTable%
    \edef\x{\pgfplotsretval}%
    \pgfplotstablegetelem{\row}{cmdoptions}\of\xTable%
    \edef\cmdoptions{\pgfplotsretval}%
    \edef\shellcmd{../isox/bin/Debug/isox\space%
      --x=\x e-3\space%
      --s=[\smin:\smax]\space%
      --h=[\hmin:\hmax]\space%
      --p=[\pmin:\pCrit]\space%
      --samples=100\space%\nSamples\space%
      \cmdoptions\space%
      > ./data/x\x e-3.dat}%
    \immediate\write18{\shellcmd}%
  }%
}%
{} % end of \ifbool{createTTables}

The file pTable.tab read in by the above file starts with this header and first entry:

p;style;label;cmdoptions
700;major p plot;normal;--samples=100 --t=[1:50]

This specifies that the 700 Pa plot is a major p plot, with a normal label. The binary for creating the isobar table is called with extra options to get 100 samples and limit the the temperature range to 1...50 °C (that helps solving the state equations).

drawGrid.tex:

% draw minor x grid lines
\foreach \s in \sMinorTicks
{
  \edef\temp{\noexpand\draw[minor grid style](axis cs:\s,\hmin) -- (axis cs:\s,\hmax);}
  \temp
}
% draw minor y grid lines
\foreach \h in \hMinorTicks
{
  \edef\temp{\noexpand\draw[minor grid style](axis cs:\smin,\h) -- (axis cs:\smax,\h);}
  \temp
}
% draw intermediate x grid lines
\foreach \s in \sInterTicks
{
  \edef\temp{\noexpand\draw[intermediate grid style](axis cs:\s,\hmin) -- (axis cs:\s,\hmax);}
  \temp
}
% draw intermediate y grid lines
\foreach \h in \hInterTicks
{
  \edef\temp{\noexpand\draw[intermediate grid style](axis cs:\smin,\h) -- (axis cs:\smax,\h);}
  \temp
}
% draw major x grid lines
\foreach \s in \sMajorTicks%
{
  \edef\temp{\noexpand\draw[major grid style](axis cs:\s,\hmin) -- (axis cs:\s,\hmax);}
  \temp
}
% draw major y grid lines
\foreach \h in \hMajorTicks
{
  \edef\temp{\noexpand\draw[major grid style](axis cs:\smin,\h) -- (axis cs:\smax,\h);}
  \temp
}

plotp.tex: (creates the pressure plots, other plot files are similar and omitted here)

\pgfplotstablegetrowsof{\pTable}
\foreach \i[evaluate=\i as \row using int(\i-1)] in {1,...,\pgfplotsretval}
{
  \pgfplotstablegetelem{\row}{p}\of\pTable
  \edef\p{\pgfplotsretval}
  \pgfplotstablegetelem{\row}{style}\of\pTable
  \edef\style{\pgfplotsretval}
  \edef\temp{\noexpand\addplot[name path global=plot-p\p Pa,\style] table[x=s,input filter] {./data/p\p Pa.dat};} \temp
}

placePLabels.tex:

\pgfkeys{/pgf/number format/.cd,std,precision=8}
\path[name path global=pLabelPathA] (axis cs:9150,2500) .. controls (axis cs:8500,3775) .. (axis cs:7500,3730);
\path[name path global=pLabelPathB] (axis cs:9160,2500) .. controls (axis cs:8510,3785) .. (axis cs:7500,3740);
\foreach \i[evaluate=\i as \row using int(\i-1)] in {2,...,52}
{
  \pgfplotstablegetelem{\row}{p}\of\pTable
  \edef\p{\pgfplotsretval}
  \pgfplotstablegetelem{\row}{pBar}\of\pTable
  \edef\pBar{\pgfplotsretval}
  \pgfplotstablegetelem{\row}{pMPa}\of\pTable
  \edef\pMPa{\pgfplotsretval}
  \pgfplotstablegetelem{\row}{label}\of\pTable
  \edef\Label{\pgfplotsretval}
  \expandafter\ifstrequal\expandafter{\Label}{short}{%
    \edef\temp{%
      \noexpand\path[name intersections={name=a,of={plot-p\p Pa and pLabelPathA}},%
        name intersections={name=b,of={plot-p\p Pa and pLabelPathB}}]%
      (a-1) -- (b-1) node[midway,p plot label] {%
        \noexpand\contour{white}{$\noexpand\pgfmathprintnumber{\pBar}$}%
      };}%
    \temp%
  }{%
  }%
  \expandafter\ifstrequal\expandafter{\Label}{normal}{%
    \edef\temp{%
      \noexpand\path[name intersections={name=a,of={plot-p\p Pa and pLabelPathA}},%
        name intersections={name=b,of={plot-p\p Pa and pLabelPathB}}]%
      (a-1) -- (b-1) node[midway,p plot label] {%
        \noexpand\contour{white}{$\noexpand\SI{\noexpand\pgfmathprintnumber{\pBar}}{\bar}$}%
      };}%
    \temp%
  }{%
  }%
  \expandafter\ifstrequal\expandafter{\Label}{long}{%
    \edef\temp{%
      \noexpand\path[name intersections={name=a,of={plot-p\p Pa and pLabelPathA}},%
        name intersections={name=b,of={plot-p\p Pa and pLabelPathB}}]%
      (a-1) -- (b-1) node[midway,p plot label] {%
        \noexpand\contour{white}{$p = \noexpand\SI{\noexpand\pgfmathprintnumber{\pBar}}{\bar}%
        = \noexpand\SI{\noexpand\pgfmathprintnumber{\pMPa}}{\mega\pascal}$}%
      };}%
    \temp%
  }{%
  }%
}
%below: #78 would be 10000 bar but that one gets an extra label
\pgfkeys{/pgf/number format/.cd,std,precision=2}
\foreach \i[evaluate=\i as \row using int(\i-1)] in {53,...,77}
{
  \pgfplotstablegetelem{\row}{p}\of\pTable
  \edef\p{\pgfplotsretval}
  \pgfplotstablegetelem{\row}{pBar}\of\pTable
  \edef\pBar{\pgfplotsretval}
  \pgfplotstablegetelem{\row}{pMPa}\of\pTable
  \edef\pMPa{\pgfplotsretval}
  \pgfplotstablegetelem{\row}{label}\of\pTable
  \edef\Label{\pgfplotsretval}
  \expandafter\ifstrequal\expandafter{\Label}{short}{%
    \edef\temp{%
      \noexpand\path[name intersections={name=a,of={plot-p\p Pa and plot-t600C}},%
        name intersections={name=b,of={plot-p\p Pa and plot-t650C}}]%
      (a-1) -- (b-1) node[midway,p plot label] {%
        \noexpand\contour{white}{$\noexpand\pgfmathprintnumber{\pBar}$}%
      };}%
    \temp%
  }{%
  }%
  \expandafter\ifstrequal\expandafter{\Label}{normal}{%
    \edef\temp{%
      \noexpand\path[name intersections={name=a,of={plot-p\p Pa and plot-t600C}},%
        name intersections={name=b,of={plot-p\p Pa and plot-t650C}}]%
      (a-1) -- (b-1) node[midway,p plot label] {%
        \noexpand\contour{white}{$\noexpand\SI{\noexpand\pgfmathprintnumber{\pBar}}{\bar}$}%
      };}%
    \temp%
  }{%
  }%
  \expandafter\ifstrequal\expandafter{\Label}{long}{%
    \edef\temp{%
      \noexpand\path[name intersections={name=a,of={plot-p\p Pa and plot-t600C}},%
        name intersections={name=b,of={plot-p\p Pa and plot-t650C}}]%
      (a-1) -- (b-1) node[midway,p plot label] {%
        \noexpand\contour{white}{$p = \noexpand\SI{\noexpand\pgfmathprintnumber{\pBar}}{\bar}%
        = \noexpand\SI{\noexpand\pgfmathprintnumber{\pMPa}}{\mega\pascal}$}%
      };}%
    \temp%
  }{%
  }%
}
% extra pCrit label:
\path[name intersections={name=a,of={plot-p22064e3Pa and plot-t600C}},%
  name intersections={name=b,of={plot-p22064e3Pa and plot-t650C}}]%
  (a-1) -- (b-1) node[midway,p plot label] {%
    \contour{white}{%
      $p = p_{crit} = \SI{\pgfmathprintnumber{220.64}}{\bar}$%
    }%
  };
% 10000 bar label:
\path (coord-t650C-start) -- (coord-t700C-start) node[midway,p plot label] {%
  \contour{white}{$\SI{\pgfmathprintnumber{10000}}{\bar}$}};
\pgfkeys{/pgf/number format/.cd,std,precision=8}
% in two-phase region:
\foreach \i[evaluate=\i as \row using int(\i-1)] in {1,...,65}
{
  \pgfplotstablegetelem{\row}{p}\of\pTable
  \edef\p{\pgfplotsretval}
  \pgfplotstablegetelem{\row}{pBar}\of\pTable
  \edef\pBar{\pgfplotsretval}
  \pgfplotstablegetelem{\row}{pMPa}\of\pTable
  \edef\pMPa{\pgfplotsretval}
  \pgfplotstablegetelem{\row}{label}\of\pTable
  \edef\Label{\pgfplotsretval}
  \expandafter\ifstrequal\expandafter{\Label}{short}{%
    \edef\temp{%
      \noexpand\path[name intersections={name=a,of={plot-p\p Pa and plot-x800m}},%
        name intersections={name=b,of={plot-p\p Pa and plot-x850m}}]%
      (a-1) -- (b-1) node[midway,p plot label] {%
        \noexpand\contour{white}{$\noexpand\pgfmathprintnumber{\pBar}$}%
      };}%
    \temp%
  }{%
  }%
  \expandafter\ifstrequal\expandafter{\Label}{normal}{%
    \edef\temp{%
      \noexpand\path[name intersections={name=a,of={plot-p\p Pa and plot-x800m}},%
        name intersections={name=b,of={plot-p\p Pa and plot-x850m}}]%
      (a-1) -- (b-1) node[midway,p plot label] {%
        \noexpand\contour{white}{$\noexpand\SI{\noexpand\pgfmathprintnumber{\pBar}}{\bar}$}%
      };}%
    \temp%
  }{%
  }%
  \expandafter\ifstrequal\expandafter{\Label}{long}{%
    \edef\temp{%
      \noexpand\path[name intersections={name=a,of={plot-p\p Pa and plot-x800m}},%
        name intersections={name=b,of={plot-p\p Pa and plot-x850m}}]%
      (a-1) -- (b-1) node[midway,p plot label] {%
        \noexpand\contour{white}{$p = \noexpand\SI{\noexpand\pgfmathprintnumber{\pBar}}{\bar}%
        = \noexpand\SI{\noexpand\pgfmathprintnumber{\pMPa}}{\mega\pascal}$}%
      };}%
    \temp%
  }{%
  }%
}

Answer 7

Nothing too spectacular, but here's one from a presentation I did recently, showing the meaning of parton distribution functions.

and a better view of the "floor":

and the TikZ source:

\documentclass[landscape]{article}

\usepackage{siunitx}
\usepackage{tikz}
\usepackage{pgfplots}
\usepackage{drawproton}

\usetikzlibrary{calc}
\usetikzlibrary{fadings}
\usetikzlibrary{shadings}
\usetikzlibrary{shadows}
\usepgfplotslibrary{units}
\pgfplotsset{compat=newest,filter discard warning=false,tick scale binop=\times}

\tikzset{
 xq2shading/.style={
  rounded corners=5pt,
  drop shadow,
  preaction={
   fill=white,
   draw=black,
   line width=0.2pt
  },
  opacity=0.15,
  top color=red!70!magenta,
  bottom color=cyan,
  middle color=red!70!magenta!50!cyan!30!white,
  shading angle=45
 }
}
% pdfdata.csv: MSTW 2008 NLO PDFs at Q^2 = 10 GeV, in 7 columns
% x Q^2 gluon up down upbar downbar
% written by Mathematica
\pgfplotstableread{datafiles/pdfdataQ210.csv}\pdfdatatableA
% pdfdata2.csv: MSTW 2008 NLO PDFs at Q^2 = 100 GeV, in 7 columns
% x Q^2 gluon up down upbar downbar
% written by Mathematica
\pgfplotstableread{datafiles/pdfdataQ2100.csv}\pdfdatatableB

\pagestyle{empty}

\begin{document}
 \begin{tikzpicture}
  \path[xq2shading] (-1.0,7.5) rectangle (10.5,-1.0);
  \draw[->,every node/.append style={above,red!70!black,rotate=90,font={\small}}] (0,-0.5) -- (0,7) node[at={(0,0)},above right] {$x=1$} node[pos=0.5] {$\ln\frac{1}{x}$} node[pos=0.9] {small $x$};
  \draw[->,every node/.append style={below,cyan!70!black,font={\small}}] (-0.5,0) -- (10,0) node[at={(0,0)},below right] {small $Q$} node[pos=0.5] {$\ln\frac{Q^2}{Q_0^2}$} node[pos=0.9] {large $Q$};

  \begin{scope}[scale=0.8,xshift=50pt,yshift=30pt]
   % the parton evolution in Q^2
   \foreach \iprotonx in {0,...,3} {
    % the parton evolution in x
    \foreach \iprotonq in {0,...,3} {
     \begin{scope}[xshift={90*\iprotonq *1pt},yshift={60*\iprotonx *1pt}]
      \pgfmathsetmacro{\partonlevel}{\iprotonx}
      \pgfmathsetmacro{\protonradius}{15 * (1 + 0.3 * sqrt(\iprotonx + 4*\iprotonq/3))}
      \drawproton[background=white,parton size decay rate={0},initial parton size={6-1.5*\iprotonq}]{\protonradius}{\partonlevel}{\partonlevel}
     \end{scope}
    }
   }
  \end{scope}
 \end{tikzpicture}

 \pagebreak

 \begin{tikzpicture}
  \begin{scope}[yscale=0.4,xslant=0.6,every node/.append style={transform shape}]
   \path[xq2shading] (-1.0,7.5) rectangle (10.5,-1.0);
   \draw[->,every node/.append style={above,red!70!black,rotate=90,font={\small}}] (0,-0.5) -- (0,7) node[at={(0,0)},above right] {$x=1$} node[pos=0.5] {$\ln\frac{1}{x}$} node[pos=0.9] {small $x$};
   \draw[->,every node/.append style={below,cyan!70!black,font={\small}}] (-0.5,0) -- (10,0) node[at={(0,0)},below right] {small $Q$} node[pos=0.5] {$\ln\frac{Q^2}{Q_0^2}$} node[pos=0.9] {large $Q$};
   \node[red!70!black] at (5,7) {high energy collisions};
   \node[cyan!70!black,rotate=-90] at (10,3.5) {high momentum transfer};

   \begin{scope}[scale=0.8,xshift=50pt,yshift=30pt]
    % the parton evolution in Q^2
    \foreach \iprotonx in {0,...,3} {
     % the parton evolution in x
     \foreach \iprotonq in {0,...,3} {
      \begin{scope}[xshift={90*\iprotonq *1pt},yshift={60*\iprotonx *1pt}]
       \pgfmathsetmacro{\partonlevel}{\iprotonx}
       \pgfmathsetmacro{\protonradius}{15 * (1 + 0.3 * sqrt(\iprotonx + 4*\iprotonq/3))}
       \drawproton[background=white,parton size decay rate={0},initial parton size={6-1.5*\iprotonq}]{\protonradius}{\partonlevel}{\partonlevel}
       \coordinate (proton\iprotonx\iprotonq) at (0,0);
      \end{scope}
     }
    }
   \end{scope}
  \end{scope}
  % final width of 108pt comes from x coordinate of (proton31)-(proton01) after transform:
  % (proton01) is at (90pt,0pt), transformed by yscale=0.4,xslant=0.6 to (90pt,0pt)
  % (proton31) is at (90pt,180pt), transformed by yscale=0.4,xslant=0.6 to (198pt,72pt)
  % 198pt-90pt = 108pt
  %
  % then yslant is chosen to map lower right coordinate of plot, (90pt+108pt,0pt),
  % to (198pt,72pt), the location of (proton31)
  % note that yslant must come before scale here
  \begin{scope}[
   yslant=0.66666666,scale=0.8,
   every axis/.append style={
    scale only axis=true,width=108pt,height=108pt,
    xmode=log,xmax=1,xmin=1e-4,ymin=1e-3,ymax=5,
    clip=false,
    axis background/.style={fill=white,fill opacity=0.7},
    x tick label style={opacity=0.5},
    x dir=reverse
   },
   overlay]
   \begin{axis}[legend to name={leg:pdflegend},legend columns=1,legend style={cells={anchor=mid west}},at={(proton01)}]
    \addplot[black,thick] table[x index=0,y index=2] {\pdfdatatableA}; % gluons
    \addplot[blue] table[x index=0,y index=3] {\pdfdatatableA}; % up
    \addplot[red] table[x index=0,y index=4] {\pdfdatatableA}; % down
    \addplot[orange] table[x index=0,y index=5] {\pdfdatatableA}; % upbar
    \addplot[green!50!black] table[x index=0,y index=6] {\pdfdatatableA}; % downbar

    \node[below left] at (rel axis cs:0.95,0.95) {\small$Q^2 = \SI{10}{GeV^2}$};
    \addlegendentry{gluon}
    \addlegendentry{up}
    \addlegendentry{down}
    \addlegendentry{antiup}
    \addlegendentry{antidown}
   \end{axis}
   \begin{axis}[at={(proton02)}]
    \addplot[black,thick,overlay] table[x index=0,y index=2] {\pdfdatatableB}; % gluons
    \addplot[blue] table[x index=0,y index=3] {\pdfdatatableB}; % up
    \addplot[red] table[x index=0,y index=4] {\pdfdatatableB}; % down
    \addplot[orange] table[x index=0,y index=5] {\pdfdatatableB}; % upbar
    \addplot[green!50!black] table[x index=0,y index=6] {\pdfdatatableB}; % downbar

    \node[below left] at (rel axis cs:0.95,0.95) {\small$Q^2 = \SI{100}{GeV^2}$};
   \end{axis}
  \end{scope}
  \path[scale=0.8] (proton01) +(0,108pt) node[above left,transform shape] {$xf(x,Q^2)$};
 \end{tikzpicture}
\end{document}

Answer 8

Probably most people don't remember what π is. The following animation will scientifically show that when a wheel rolls one lap without slipping, it travels a distance of 3++ times of its diameter.

\documentclass[pstricks,border=12pt,12pt]{standalone}
\usepackage{pst-plot}
\psset{unit=2cm,dimen=m}
\newdimen\Width\Width=3.64159265\psxunit

\begin{document}
\multido{\i=0+10}{19}{%
\begin{pspicture}(-.5,-.2)(\Width,1)
    \psaxes[yAxis=false](0,0)(-.5,0)(\Width,0)
    \multips(.5,.5)(1,0){3}{\pscircle[linecolor=cyan!20]{.5}}
    \pstVerb{/length {\i\space DegtoRad} def /angle {\i\space .5 div 90 add neg} def}
    \rput(!length .5){\psline{->}(!.5 angle PtoC)}
    \ifnum\i=180\color{red}\psxTick[labelsep=1pt](3.14159265){\pi}\fi
    \psset{linewidth=2pt}
    \pscircle(!length .5){.5}
    \psline[linecolor=red](!length 0)
    \psarcn[linecolor=red](!length .5){.5}{-90}{!angle}
\end{pspicture}}
\end{document}

Answer 9

Inspired by @Paul Gessler, the following is a statics problem from a class I taught. The problem was to find the maximum weight the crane could carry as a function of distance before it would tip over (the supports at D and E aren't bolted to the ground). It uses the drawing and plotting capabilities of TiKZ to draw the crane and the solution. Looking back, it seems like there must be an easier way to draw the superstructure...

\documentclass[tikz]{standalone}
\begin{document}
\begin{tikzpicture}[scale=0.5]
\draw (-4,0) -- (40,0);
\draw[double] (0,0) -- ++(1.5,0.5)--++(3,0)--++(1.5,-0.5);
\draw[double] (0,0) -- ++(1.5,1.5) ++(3,0)--++(1.5,-1.5);
\draw[double] (1.5,0.5) -- ++(0,10)--++(3,0)--++(0,-10);
\draw[double,join=bevel] (1.5,0.5) -- ++(18.43:3.16) -- ++(161.57:3.16) -- ++(18.43:3.16) -- ++(161.57:3.16) -- ++(18.43:3.16) -- ++(161.57:3.16) -- ++(18.43:3.16) -- ++(161.57:3.16) -- ++(18.43:3.16) -- ++(161.57:3.16);
\draw[double] (1.5,0.5) -- +(135:0.707);
\draw[double] (4.5,0.5) -- +(45:0.707);
\draw[fill=lightgray] (-1,8.5) rectangle (-3,14) node at +(1,-2.75) {$A$};
\draw[double] (-1,10.5) -- ++(40,0) -- ++(0,1.732) -- ++(-40,0);
\draw[double,join=bevel] (-1,10.5+1.732) -- ++(-60:2) -- ++(60:2) -- ++(-60:2) -- ++(60:2) -- ++(-60:2) -- ++(60:2) -- ++(-60:2) -- ++(60:2) -- ++(-60:2) -- ++(60:2) -- ++(-60:2) -- ++(60:2) -- ++(-60:2) -- ++(60:2) -- ++(-60:2) -- ++(60:2) -- ++(-60:2) -- ++(60:2) -- ++(-60:2) -- ++(60:2) -- ++(-60:2) -- ++(60:2) -- ++(-60:2) -- ++(60:2) -- ++(-60:2) -- ++(60:2) -- ++(-60:2) -- ++(60:2) -- ++(-60:2) -- ++(60:2) -- ++(-60:2) -- ++(60:2) -- ++(-60:2) -- ++(60:2) -- ++(-60:2) -- ++(60:2) -- ++(-60:2) -- ++(60:2) -- ++(-60:2) -- ++(60:2) node at +(0.75,-1.723/2) {$B$};
\draw[fill=lightgray] (4.6,10.5) rectangle (39.1,9.5);
\draw[double] (0,10.5) -- ++(0,-1.5) -- +(1.5,0);
\draw[double] (0,9) -- +(45:2.121);
\draw[fill=gray] (-0.6,13) rectangle (0.6,10.5+1.732);
\draw[fill=lightgray, even odd rule] (18.5,5) circle (0.25) circle (0.125);
\draw[double distance=0.4] (-0.5,13) -- ++(0,-4) ++(0.5,-0.5) -- ++(18,0) ++(0.5,-0.5) -- ++(0,-3);
\draw (18,8.55) arc (90:0:0.55);
\draw[fill=white] (18,8) circle (0.5);
\draw[color=white] (4.6,9.75) -- (39.1,9.75);
\draw[fill=white] (18.625,10.125) circle (0.375) +(-1.25,0) circle (0.375);
\draw[rounded corners, fill=lightgray] (18,7.5) -- (19,10.375) -- ++(-2,0) -- cycle;
\draw (18,8) circle (0.07);
\draw (18.625,10.125) circle (0.07) +(-1.25,0) circle (0.07);
\draw (-0.55,9) arc (180:270:0.55);
\draw[fill=gray] (0,9) circle (0.5) circle (0.07) node at +(0,-1.25) {$C$};
\draw[fill=gray] (0,13) circle (0.6) circle (0.07) node at +(1.25,0) {$M$};
\draw[double] (18.5,5) -- +(3,-1) (18.5,5) -- +(-3,-1);
\draw[fill=gray] (15.5,4.05) rectangle (21.5,3.755);
\draw[fill=red] (17,4.06) rectangle +(0.5,0.3);
\draw[fill=red] (17.5,4.06) rectangle +(0.5,0.3);
\draw[fill=red] (18,4.06) rectangle +(0.5,0.3);
\draw[fill=red] (18.5,4.06) rectangle +(0.5,0.3);
\draw[fill=red] (19,4.06) rectangle +(0.5,0.3);
\draw[fill=red] (19.5,4.06) rectangle +(0.5,0.3);
\draw[fill=red] (17.5,4.37) rectangle +(0.5,0.3);
\draw[fill=red] (18,4.37) rectangle +(0.5,0.3);
\draw[fill=red] (18.5,4.37) rectangle +(0.5,0.3);
\draw[fill=red] (19,4.37) rectangle +(0.5,0.3);
%Dimensions
\draw[semithick] (0,-0.25) -- +(0,-1) node at +(0,1.25) {$D$} ++(3,-3) -- +(0,3.25+10.5+1.723) ++(3,3) -- +(0,-1) node at +(0,1.25) {$E$} ++(33,-3) -- +(0,12.25);
\draw[semithick] (3,10.75+1.732) -- (3,13.6+0.25+1+1.5) ++(-3,-1.5) -- +(0,-1);
\draw[semithick] (-2,14.25) -- (-2,13.6+0.25+1+1.5);
\draw[semithick] (9,6)--++(0,2.25) ++(0,0.5)--(9,9.95);
\draw[semithick] (18.5,2) -- +(0,1);
\fill (9,10.5) -- ++(0.3,0) arc (0:-90:0.3) -- ++(0,0.6) arc (90:180:0.3);
\fill[white] (9,10.5) -- ++(0.3,0) arc (0:90:0.3) -- ++(0,-0.6) arc (270:180:0.3);
\draw[very thin] (9,10.5) circle (0.3) node at +(0,2.5) {$G$};
\draw[semithick, to-to] (0, -0.75) -- +(3,0) node[font=\footnotesize] at +(1.5,-0.5) {3 m};
\draw[semithick, to-to] (3, -0.75) -- +(3,0) node[font=\footnotesize] at +(1.5,-0.5) {3 m};
\draw[semithick, to-to] (3, -2.5) -- +(36,0) node[fill=white, font=\footnotesize] at +(18,0) {36 m};
\draw[semithick, to-to] (3,13.6+0.25+0.5) -- +(-3,0) node[font=\footnotesize] at +(-1.5,0.5) {3 m};
\draw[semithick, to-to] (3,13.6+0.25+2) -- +(-5,0) node[font=\footnotesize] at +(-2.5,0.5) {5 m};
\draw[semithick,to-to] (3,6.5) -- +(6,0) node[fill=white, font=\footnotesize] at +(3,0) {6 m};
\draw[semithick,to-to] (3,2.5) -- +(15.5,0) node[fill=white,font=\footnotesize] at +(7.75,0) {$x$};
\end{tikzpicture}
\begin{tikzpicture}[domain=0:36,x=100, y=20, scale=0.1]
    \draw[very thin,color=gray] (0,0) grid[xstep=5,ystep=20] (36,140);
    \foreach \x in {0,5,...,35}
        \draw (\x,1) -- (\x,-1)
            node[anchor=north] {\x};
\foreach \y in {0,20,...,140}
        \draw (0.5,\y) -- (-0.5,\y)
            node[anchor=east] {\y};
    \draw[->] (0,0) -- (36,0) node at +(-18,-12) {$x$ (m)}; 
    \draw[->] (0,0) -- (0,140) node[rotate=90] at +(-3,-70) {Weight (kN)};
    \draw[color=red,domain=4.5:36, smooth, semithick] plot (\x,{209/(\x-3)}) node[right] {$W_{max}$};
\end{tikzpicture}
\end{document}

Answer 10

This very same image was not used in a publication. I copied the idea from a journal article and remade it using PSTricks and pst-optexp:

\documentclass{standalone}
\usepackage{pst-optexp}
\begin{document}
\begin{pspicture}(-0.2,0)(12.3,8.8)
\newpsobject{laser}{optbox}{position=start, innerlabel}
\psset[optexp]{lens=2, phwidth=0.07, outerheight=0.6}
\pnode(1,7){L}\pnode([offset=-6]L){PSLM}
\pnode([Xnodesep=2,offset=1]L){ASLM}\pnode([offset=-0.5,Xnodesep=9]L){MRef}
\pnode([offset=-7]ASLM){ML}\pnode([Xnodesep=8.5]ML){Cam}
\begin{optexp}
  \laser[optboxsize=1.6 0.6](L)(PSLM){Nd:YAG}
  \beamsplitter[bssize=0.4, labelangle=-90](L)(L|MRef)(MRef){BS}
  \lens[abspos=1.2, lens=0.5 0.5 0.4, n=2.5, labelangle=-10](L)(PSLM){MO}
  \pinhole[abspos=1.4, labelangle=10](L)(PSLM){PH}
  \lens[abspos=2.3](L)(PSLM){L}
  \opttripole[label=0.5](L)(PSLM)(ASLM){\psframe[dimen=outer](-0.5,0)(0.5,0.1)}{PSLM}
  \lens[label=0.6 -40](PSLM)(ASLM){L}
  \opttripole[label=0.5](PSLM)(ASLM)(ML){\psframe[dimen=outer](-0.5,0)(0.5,0.1)}{ASLM}
  \lens[position=0.45, labelangle=180](ASLM)(ML){L}
  \optretplate[labelangle=180, position=0.55](ASLM)(ML){$\lambda/2$}
  \optplate[labelangle=180, position=0.62](ASLM)(ML){P}
  \mirror[labeloffset=0.4](ASLM)(ML)(Cam){M}
  \newpsstyle{Beam}{fillcolor=green!80!black, opacity=0.5, fillstyle=solid, linestyle=none, beaminside=false}
  \drawwidebeam[beamwidth=0.1, stopinside]{1-5}
  \psset{loadbeampoints}
  \drawwidebeam[stopinside, savebeampoints=2]{5-7}
  \drawwidebeam[loadbeampoints=2, beamdiv=-8.5]{7-8}
  \drawwidebeam[loadbeampoints=2, beamdiv=-8.5, beamangle=-4]{7-8}
  \drawwidebeam[beamdiv=-8.5, beamangle=-4.5]{8-9}
  \drawwidebeam[loadbeampoints=2, beamdiv=-8.5, beamangle=4]{7-8}
  \drawwidebeam[beamdiv=-8.5, beamangle=4.5]{8-9}
  \lens[abspos=2](ML)(Cam){L}
  \lens[abspos=4](ML)(Cam){L}
  \crystal[abspos=6, voltage, crystalsize=1 0.6, fillcolor=yellow!90!black, fillstyle=solid](ML)(Cam){SBN}
  \beamsplitter[bssize=0.6](MRef)(MRef|Cam)(Cam){BS}
  \lens[n=2.4](MRef|Cam)(Cam){L}
  \optbox[optboxsize=0.8 0.6, position=end](ML)(Cam){Cam}
  \drawwidebeam[savebeampoints=2, stopinside]{9-13}
  \drawwidebeam[loadbeampoints=2, beamdiv=-16, beamangle=5, stopinside]{13-14}
  \drawwidebeam[beamangle=-5]{14-18}
  \drawwidebeam[loadbeampoints=2, beamdiv=-16, beamangle=-5, stopinside]{13-14}
  \drawwidebeam[beamangle=5]{14-18}
  \lens[lens=0.5 0.5 0.4, n=2](L|MRef)(MRef){MO}
  \pinhole[position=0.53, labelangle=180](L|MRef)(MRef){PH}
  \lens[position=0.65](L|MRef)(MRef){L}
  \optplate[position=0.7](L|MRef)(MRef){S}
  \mirror[labeloffset=0.4](L|MRef)(MRef)(MRef|Cam){M}
  \addtopsstyle{Beam}{fillcolor=red!70}
  \drawwidebeam[loadbeampoints=false, beamwidth=0.1, savebeampoints]{2}{19-21}
  \drawwidebeam{21-23}{16-18}
\end{optexp}
\end{pspicture}
\end{document}

Answer 11

Manuel Luque's Syracuse website has a number of neat technical examples that includes some animations (forgive the loading; images/animations are linked to the source):

Answer 12

The scientific viewpoint of an egg on the frying pan.

\documentclass[pstricks]{standalone}
\usepackage{pst-node,pst-plot}
\pstVerb{realtime srand}

\begin{document}
\psLoop{25}{%
\begin{pspicture}(-2,-2)(2,2)
    \pscircle*[linecolor=orange]{0.75}
    \curvepnodes[plotpoints=73]{0}{360}{Rand 10 div 1.50 add t PtoC}{P}
    \psnccurve(0,\numexpr\Pnodecount-1){P}
\end{pspicture}}
\end{document}

Answer 13

For those who study radar imaging, the following should be relevant.

\documentclass[pstricks,border=12pt]{standalone}
\usepackage{multido}
\SpecialCoor
\psset{dimen=monkey}

\definecolor{radar}{RGB}{77,255,116}
\newpsstyle{wedge}{linestyle=none,linewidth=0,fillstyle=solid,fillcolor=radar}
\newpsstyle{beam}{linewidth=.5pt,linecolor=radar}
\newpsstyle{axes}{linewidth=.3pt,linecolor=radar!10!black}

\def\wiper#1{\rput{-#1}{\multido{\i=0+2,\r=.400+-.008}{50}{\psline[style=beam](3,0)\pswedge[style=wedge,opacity=\r](0,0){3}{\i}{!\i\space 2 add}}}}
\def\axes{\multido{\r=.5+.5}{6}{\pscircle[style=axes]{\r}}\multido{\i=0+30}{12}{\psline[style=axes](3;\i)}}


\newenvironment{objects}[1]
{\psframe*(-3,-3)(3,3)\psclip{\rput{-#1}{\pswedge[linestyle=none,linewidth=0](0,0){3}{0}{100}}}\ignorespaces}
{\endpsclip\ignorespacesafterend}

\usepackage{graphicx}

\begin{document}
\multido{\ia=0+15}{24}{
\begin{pspicture}(-3,-3)(3,3)
    \begin{objects}{\ia}
        \rput(0,-2.25){\textcolor{radar}{\large PSTricks attack}}
        \rput(1.5;135){\includegraphics[scale=.1]{alien}}
    \end{objects}
    \axes
    \wiper{\ia}%
\end{pspicture}}
\end{document}

Answer 14

This is one I like from my thesis. It illustrates the predicted boundaries for boundary layer transition mechanisms on a cylindrical afterbody at incidence: (1) free shear-layer instability, (2) attachment-line instability, (3) cross-flow instability, (4) streamwise-flow instability.

\documentclass{standalone}
\usepackage{calc,pgfplots}
      \pgfplotsset{compat=1.7}

\begin{document}

%% free shear-layer instability (fsli)
\pgfmathdeclarefunction{fsli}{1}{%
  \pgfmathparse{ tan(#1)/( cos(#1)*( 1 + 3.3*((tan(#1))^2) ) ) }%
}%
%
%% attachment-line instability (ali)
\pgfmathdeclarefunction{ali}{1}{%
  \pgfmathparse{ 1.1*tan(#1)*(1/cos(#1)) }%
}%
%
%% cross-flow instability (csi)
\pgfmathdeclarefunction{csi}{1}{%
  \pgfmathparse{ 0.145*( ( 1 + 3.3*(tan(#1))^2 ) / sin(#1) ) }%
}%
%
%% streamwise-flow instability (sfi)
\pgfmathdeclarefunction{sfi}{1}{%
  \pgfmathparse{ 4 }%
}%
%
%% piecewise function (combining ali, csi and sfi)
\pgfmathdeclarefunction{alicsisfi}{1}{%
  \pgfmathparse{%
    (and( #1>=1    , #1<=25.78) * ( ali(x) ) +%
    (and( #1>25.78 , #1<=70.00) * ( csi(x) ) +%
                (and( #1>70.00 , #1<=89.99) * ( sfi(x) )  %
   }%
}%



\begin{tikzpicture}

% set style options for annotations with pins (see bottom of tikzpicture)
\tikzset{%
   every pin/.style={draw=none,
                     fill=none,
                     %rectangle,rounded corners=0pt,
                     font=\scriptsize}
                 }

\begin{semilogyaxis}[%
%
view={0}{90},
width=0.50\linewidth,height=0.75\linewidth,
%
scale only axis,
axis on top=false,
axis lines*=box,
%
xmin=0, xmax=90,
xtick={0,10,20,30,40,50,60,70,80,90},
xlabel={\raisebox{0pt}[\height][\depth]{$\alpha$ (deg)}},
%
ymin=0.1, ymax=10,
ytick={0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9,1.0,2,3,4,5,6,7,8,9,10},
yticklabels={0.1,0.2,{},0.4,{},0.6,{},0.8,{},1.0,2,{},4,{},6,{},8,{},10},
ylabel={\raisebox{0pt}[\height][\depth]{$R_D \times 10^{6}$}},
]



%% fsli (start stacking)
\addplot[
domain=1:89.99,samples=225,
draw=none,fill=none,mark=none,
stack plots=y]
{ fsli(x) };
%
%% stack difference between alicsisfi (upper) and fsli (lower) curves on top of fsli and fill area
\addplot[
domain=1:89.99,samples=225,
draw=none,
fill=black!10,
stack plots=y]
{ max( alicsisfi(x) - fsli(x) , 0 ) } % area above fsli and below alicsisfi
\closedcycle;



%% fsli, alpha = [1 , 89.99]
\addplot[
domain=1:89.99,samples=225,
solid,line width=0.8pt,draw=black,mark=none]
{ fsli(x) };



%% ali (1), alpha = [1 , 25.78]
\addplot[
domain=1:25.78,samples=62,
solid,line width=0.8pt,draw=black,mark=none]
{ ali(x) };
%
%% ali (2), alpha = [25.78 , 89.99]
\addplot[
domain=25.78:89.99,samples=163,
dashed,draw=black,mark=none]
{ ali(x) };



%% csi (1), alpha = [1 , 25.78]
\addplot[
domain=1:89.99,samples=62,
dashed,draw=black,mark=none]
{ csi(x) };
%
%% csi (2), alpha = [25.78 , 70]
\addplot[
domain=25.78:70,samples=112,
solid,line width=0.8pt,draw=black,mark=none]
{ csi(x) };
%
%% csi (3), alpha = [70 , 89.99]
\addplot[
domain=70:89.99,samples=174,
dashed,draw=black,mark=none]
{ csi(x) };



%% sfi (1), alpha = [1 , 70]
\addplot[
domain=1:70,samples=350,
dashed,draw=black,mark=none]
{ sfi(x) };
%
%% sfi (2), alpha = [70 , 89.99]
\addplot[
domain=70:89.99,samples=51,
solid,line width=0.8pt,draw=black,mark=none]
{ sfi(x) };


%% annotations (see style options for pins set with \tikzset above)
\node[coordinate,pin=-95:{1}] at (axis cs:50,0.326) {};
\node[coordinate,pin=-30:{2}] at (axis cs:23.3,0.5158) {};
\node[coordinate,pin=below right:{3}] at (axis cs:52.3,1.196) {};
\node[coordinate,pin=80:{4}] at (axis cs:77.5,4) {};
%
\node[draw=black,fill=white] at (axis cs:47,0.16) {\emph{laminar regime}};
\node[draw=black,fill=white] at (axis cs:60,0.52) {\emph{short bubble regime}};
\node[draw=black,fill=white] at (axis cs:30,3.95) {\emph{turbulent regime}};

\end{semilogyaxis}

\end{tikzpicture}

\end{document}

Answer 15

Maybe not my best, but one I quite like.

The figure has been made for a publication below about increasing the field of view of microtomographic scans and can be found in doi:10.1107/S0909049510019618.

As with pretty much all my figures, it's made with the help of tikz, pgfplots, siunitx, my script to calculate and place scalebars, lots of trial and error and sometimes with help from tex.SE...

The image is a screenshot from my thesis (made with classicthesis), thus the different font.

\documentclass{article}

\usepackage[demo]{graphicx}
\usepackage{subfig}
\usepackage{tikz}
\usepackage{pgfplots}
\usepackage{siunitx}
\usepackage{hyperref}

\newcommand{\imsize}{\linewidth}
\newlength\imagewidth % needed for scalebars
\newlength\imagescale % ditto

\begin{document}

\renewcommand{\imsize}{.47\linewidth}%
\pgfmathsetlength{\imagewidth}{\imsize}% desired display width of image
\pgfmathsetlength{\imagescale}{\imagewidth/1024}% pixel width of image
\begin{figure}[p]%
    \noindent\makebox[\textwidth]{%
        \subfloat[Projections from subscans]{%
            \begin{tikzpicture}[x=\imagescale,y=-\imagescale]%
                \node[anchor=north west, inner sep=0pt, outer sep=0pt] at (0,0) {\includegraphics[width=\imagewidth]{img/Haberthuer2010/R108C21Cb_s13358_normalize}};%
                \def\overlap{141}%
                \fill [red, nearly transparent] (1024-\overlap,1) rectangle (1024,1024);%
                \draw (1024-\overlap,1) rectangle (1024,1024);%
            \end{tikzpicture}%
            \begin{tikzpicture}[x=\imagescale,y=-\imagescale]%
                \node[anchor=north west, inner sep=0pt, outer sep=0pt] at (0,0) {\includegraphics[width=\imagewidth]{img/Haberthuer2010/R108C21Cb_s23358_normalize}};%
                \def\overlap{141}%
                \fill [green, nearly transparent] (1,1) rectangle (\overlap,1024);%
                \draw (1,1) rectangle (\overlap,1024);%
                \def\overlap{138}%
                \fill [blue, nearly transparent] (1024-\overlap,1) rectangle (1024,1024);%
                \draw (1024-\overlap,1) rectangle (1024,1024);%
            \end{tikzpicture}%
            \begin{tikzpicture}[x=\imagescale,y=-\imagescale]%
                \node[anchor=north west, inner sep=0pt, outer sep=0pt] at (0,0) {\includegraphics[width=\imagewidth]{img/Haberthuer2010/R108C21Cb_s33358_normalize}};%
                \def\overlap{138}%
                \fill [yellow, nearly transparent] (1,1) rectangle (\overlap,1024);%
                \draw (1,1) rectangle (\overlap,1024);%
                \def\x{924}% 1024 - 100
                \def\y{922}% 1024 * .9 = 921.6
                \def\bar{338}% 100 px = 148 um
                \draw[|-|,thick, color=white] (\x-\bar,\y) -- (\x,\y) node [midway, above] {\SI{500}{\micro\meter}};%
            \end{tikzpicture}%
            \label{subfig:workflow-projections}%
        }%
    }%
    \\%
    \renewcommand{\imsize}{1.41\linewidth}%
    \pgfmathsetlength{\imagewidth}{\imsize}% desired displayed width of image
    \pgfmathsetlength{\imagescale}{\imagewidth/2793}% pixel width of image
    \noindent\makebox[\textwidth]{%
        \subfloat[Merged and corrected projection]{%
            \begin{tikzpicture}[x=\imagescale,y=-\imagescale]%
                \node[anchor=north west, inner sep=0pt, outer sep=0pt] at (0,0) {\includegraphics[width=\imagewidth]{img/Haberthuer2010/R108C21Cb_mrg3333_normalize}};%
                \def\x{2693} % 2793-100
                \def\y{922} % 1024*.9 = 921.6
                \def\bar{338} % 100 px = 148 um
                \draw[|-|,thick, color=white] (\x-\bar,\y) -- (\x,\y) node [midway, above] {\SI{500}{\micro\meter}};
            \end{tikzpicture}%
            \label{subfig:workflow-merge}%
        }%
    }%
    \\%
    \pgfmathsetlength{\imagescale}{\imagewidth/2792}% pixel width of image
    \noindent\makebox[\textwidth]{%
        \subfloat[Reconstruction]{%
            \begin{tikzpicture}[x=\imagescale,y=-\imagescale]%
                \node [anchor=north west, inner sep=0pt, outer sep=0pt] at (0,0) {\includegraphics[width=\imagewidth]{img/Haberthuer2010/R108C21Cb_mrg1024rec8bit}};
                \clip (0,0) rectangle (2792,992);               
                \def\x{2692}% 2792-100
                \def\y{893}% 992 * .9 = 892.8
                \def\bar{338}% 100 px = 148 um
                %%%% scalebar
                    \draw[|-|,thick, color=white] (\x-\bar,\y) -- (\x,\y) node [midway, above] {\SI{500}{\micro\meter}};
                %%%% big circle
                    \draw [dashed, ultra thick, color=red] (2792/2,992/2) circle (512);
                    \def\angle{35}
                    \draw [white, thick, <->] (2792/2,992/2) +(\angle:0) -- node (bigto) {} +(\angle:512); 
                    \node [white] (bigfrom) at (349,256){$\frac{1024}{2}$px};
                    \draw [white, ->, thick, densely dotted] (bigfrom) to [bend left=45] (bigto);
                %%%% big circle
                %%%% 141px circle
                \draw [dashed, ultra thick, color=red] (2792/2,992/2) circle (512-141);
                \def\angle{35+90}
                    \draw [white, thick,<->] (2792/2,992/2) +(\angle:0) -- node (smallto) {} +(\angle:512-141);
                    \node [white] (smallfrom) at (349,384) {$\frac{1024}{2}-141$px};
                    \draw [white, ->, thick, densely dotted] (smallfrom) to [bend left=45] (smallto);
                %%%% 141px circle                   
                %%%% center
                \fill [color=red] (2792/2,992/2) circle (5);
                %%%% center
            \end{tikzpicture}%
            \label{subfig:workflow-reconstruction}%
        }%
    }%
    \caption[Workflow of a wide field scan]{Workflow of a wide field scan. The images show a rat lung sample from a Sprague-Dawley rat, obtained 21 days after birth, scanned with the acquisition protocol B (see \autoref{tab:protocols}). %
            \subref{subfig:workflow-projections}: Three corrected and independently acquired projections from subscans $s_1$--$s_3$ are shown. Each one is 1024\(\times\)1024 pixels large and covers a field of view of \SI{1.52}{\milli\meter}. Subscans $s_1$ and $s_2$ overlap by 141 pixels (red and green overlay), subscans $s_2$ and $s_3$ overlap by 138 pixels (blue and yellow overlay). %
            \subref{subfig:workflow-merge}: Merged projection obtained from the three subscans shown in subfigure \subref{subfig:workflow-projections}. Each merged projection has a size of 2792\(\times\)1024 pixels. Due to the overlap required to merge the projections, the width of the merged projections is slightly smaller than three times the width of the subscans. %
            \subref{subfig:workflow-reconstruction}: Cropped slice of the reconstructed tomographic dataset. The dashed red circles mark the start and end of the overlap region.}
    \label{fig:wide-field-scan-results}
\end{figure}%

\end{document}

Answer 16

Transformer

\documentclass{article}

\usepackage[
  hmargin = 2.4cm,
  vmargin = 3cm
]{geometry}
\usepackage[
  figureposition = bottom
]{caption}
\usepackage{pst-solides3d}

% Upright text as subscript in math mode.
\makeatletter
 \begingroup
  \catcode`\_=\active
  \protected\gdef_{\@ifnextchar|\subtextup\sb}
 \endgroup
\def\subtextup|#1|{\sb{\textup{#1}}}
\AtBeginDocument{\catcode`\_=12 \mathcode`\_=32768}
\makeatother

% Setup of caption.
\DeclareCaptionLabelSeparator{adjustment}{:\quad}
\captionsetup{
  font = small,
  labelfont = sc,
  labelsep = adjustment,
  width = 0.7\textwidth
}

%% Parameters
% Windings
\def\lWind{40}
\def\rWind{80}
% Radii
\def\rHelix{1.13}
\def\rWire{0.004}

% Constants
\def\factor{160} % \factor > \lWind,\rWind
\pstVerb{%
  /left 2 \lWind\space mul \factor\space div def
  /right 2 \rWind\space mul \factor\space div def
}

%% Colours
\colorlet{wireColor}{red!60}
\colorlet{coreColor}{cyan!50}
%% Wire
\newpsobject{wire}{psSolid}{%
  object = courbe,
  ngrid = 4365 left mul cvi 5,
  r = \rWire,
  fillcolor = wireColor,
  incolor = wireColor
}

\pagestyle{empty}

\begin{document}

\begin{figure}[htbp]
 \centering
  \begin{pspicture}(-6.6,-4.4)(6.6,4.2)
   \psset{%
     algebraic,
     solidmemory,
     viewpoint = 20 5 10 rtp2xyz,
     lightsrc = 20 60 60 rtp2xyz,
     Decran = 30,
     grid = false,
     action = none
   }
   %%--------- Core ----------
   \psSolid[
     object = anneau,
     h = 1.0,
     R = 4,
     r = 2.5,
     ngrid = 4,
     RotX = 90,
     RotY = 45,
     RotZ = 90,
     fillcolor = coreColor,
     name = core
   ]
   %%--------- Wire ----------
   % Left
   \defFunction{heliceA}(t){\rHelix*cos(\factor*t)}{\rHelix*sin(\factor*t)}{t/left}
   \wire[
     function = heliceA,
     range = 0 Pi left mul,
     name = wireA
   ](0,-2.25,-1.5)
   % Right
   \defFunction{heliceB}(t){\rHelix*cos(\factor*t)}{-\rHelix*sin(\factor*t)}{t/right}
   \wire[
     function = heliceB,
     range = 0 Pi right mul,
     name = wireB
   ](0,2.25,-1.5)
   %%------- Assembly --------
   \psSolid[
     object = fusion,
     base = core wireA wireB,
     action = draw**
   ]
   %%---- Connecting wire ----
   % Left
   \psline[
     linewidth = 1.5pt
   ](-6.8,2.71)(-3.705,2.71)(-3.705,2.31)
   \psline[
     linewidth = 1.5pt
   ](-6.8,-2.845)(-3.65,-2.845)(-3.65,-2.545)
   \pcline[
     linewidth = 0.5pt
   ]{<->}(-6,2.71)(-6,-2.845)
   \ncput*{\small $U_|p|$}
   \uput[315](-6,2.71){\small $+$}
   \uput[40](-6,-2.845){\small $-$}
   \psline{->}(-6.8,3.01)(-5.5,3.01)
   \uput[0](-5.5,3.01){\small $I_|p|$}
   \rput(-1.3,0){\small $N_|p|$}
   % Right
   \psline[
     linewidth = 1.5pt
   ](6.8,2.65)(3.48,2.65)(3.48,2.25)
   \psline[
     linewidth = 1.5pt
   ](6.8,-3.0)(3.41,-3)(3.41,-2.7)
   \pcline[
     linewidth = 0.5pt
   ]{<->}(6,2.65)(6,-3)
   \ncput*{\small $U_|s|$}
   \uput[225](6,2.65){\small $+$}
   \uput[140](6,-3){\small $-$}
   \psline{->}(5.5,2.95)(6.8,2.95)
   \uput[180](5.5,2.95){\small $I_|s|$}
   \rput(1.3,0){\small $N_|s|$}
  \end{pspicture}
 \caption{Transformer with $\lWind$~windings on the primary side and $\rWind$~windings on the secondary side.}
 \label{fig:transformer}
\end{figure}

\end{document}

Answer 17

I don't know the name of this illusion but the important thing is that it is about simple harmonic motion of equally-spaced points with equally-spaced phase difference. Enjoy! The same code was posted here.

\documentclass[preview,border=12pt,multi]{standalone}
\usepackage{pstricks}

\psset{unit=.3}

% static point
% #1 : half of the number of points
% #2 : ith point
\def\x[#1,#2]{(3*cos(Pi/#1*#2))}
\def\y[#1,#2]{(3*sin(Pi/#1*#2))}

% oscillated point
% #1 : half of the number of points
% #2 : ith point
% #3 : time parameter
\def\X[#1,#2]#3{(\x[#1,#2]*cos(#3+Pi/#1*#2))}
\def\Y[#1,#2]#3{(\y[#1,#2]*cos(#3+Pi/#1*#2))}

% single frame
% #1 : half of the number of points
% #2 : time parameter
\def\Frame#1#2{%
\begin{pspicture}(-3,-3)(3,3)
    \pstVerb{/I2P {AlgParser cvx exec} bind def}%
    \pscircle*{\dimexpr3\psunit+2pt\relax}
    \foreach \i in {1,...,#1}{\psline[linecolor=yellow](!\x[#1,\i] I2P \y[#1,\i] I2P)(!\x[#1,\i] I2P neg \y[#1,\i] I2P neg)}
    \foreach \i in {1,...,#1}{\pscircle*[linecolor=white](!\X[#1,\i]{#2} I2P \Y[#1,\i]{#2} I2P){2pt}}   
\end{pspicture}}

\begin{document}
\foreach \t in {0,...,24}
{   
    \preview
    \Frame{1}{2*Pi*\t/25} \quad \Frame{2}{2*Pi*\t/25} \quad \Frame{3}{2*Pi*\t/25} \quad \Frame{5}{2*Pi*\t/25} \quad \Frame{10}{2*Pi*\t/25}
    \endpreview
}
\end{document}

Answer 18

The following is a TikZ version of a three-tier data center architecture (the reference was Figure 3-8 Three-Tier Model with 8-Way ECMP of Cisco Data Center Infrastructure 2.5 Design Guide). The code is ugly, unreadable so take it as it is. Though, it is highly inspired by Q/A of the site: some of you may recognize your own piece of code somewhere.

The code:

\documentclass[tikz,border=5pt,png]{standalone}
\usepackage{pgfplots}
\pgfplotsset{compat=1.9}
\usetikzlibrary{backgrounds,calc,shadings,shapes.arrows,shapes.symbols,shadows}
\definecolor{switch}{HTML}{006996}

% argument #1: any options
\newenvironment{customlegend}[1][]{%
    \begingroup
    % inits/clears the lists (which might be populated from previous
    % axes):
    \csname pgfplots@init@cleared@structures\endcsname
    \pgfplotsset{#1}%
}{%
    % draws the legend:
    \csname pgfplots@createlegend\endcsname
    \endgroup
}%

% makes \addlegendimage available (typically only available within an
% axis environment):
\def\addlegendimage{\csname pgfplots@addlegendimage\endcsname}

\makeatletter
\pgfkeys{/pgf/.cd,
  parallelepiped offset x/.initial=2mm,
  parallelepiped offset y/.initial=2mm
}
\pgfdeclareshape{parallelepiped}
{
  \inheritsavedanchors[from=rectangle] % this is nearly a rectangle
  \inheritanchorborder[from=rectangle]
  \inheritanchor[from=rectangle]{north}
  \inheritanchor[from=rectangle]{north west}
  \inheritanchor[from=rectangle]{north east}
  \inheritanchor[from=rectangle]{center}
  \inheritanchor[from=rectangle]{west}
  \inheritanchor[from=rectangle]{east}
  \inheritanchor[from=rectangle]{mid}
  \inheritanchor[from=rectangle]{mid west}
  \inheritanchor[from=rectangle]{mid east}
  \inheritanchor[from=rectangle]{base}
  \inheritanchor[from=rectangle]{base west}
  \inheritanchor[from=rectangle]{base east}
  \inheritanchor[from=rectangle]{south}
  \inheritanchor[from=rectangle]{south west}
  \inheritanchor[from=rectangle]{south east}
  \backgroundpath{
    % store lower right in xa/ya and upper right in xb/yb
    \southwest \pgf@xa=\pgf@x \pgf@ya=\pgf@y
    \northeast \pgf@xb=\pgf@x \pgf@yb=\pgf@y
    \pgfmathsetlength\pgfutil@tempdima{\pgfkeysvalueof{/pgf/parallelepiped offset x}}
    \pgfmathsetlength\pgfutil@tempdimb{\pgfkeysvalueof{/pgf/parallelepiped offset y}}
    \def\ppd@offset{\pgfpoint{\pgfutil@tempdima}{\pgfutil@tempdimb}}
    \pgfpathmoveto{\pgfqpoint{\pgf@xa}{\pgf@ya}}
    \pgfpathlineto{\pgfqpoint{\pgf@xb}{\pgf@ya}}
    \pgfpathlineto{\pgfqpoint{\pgf@xb}{\pgf@yb}}
    \pgfpathlineto{\pgfqpoint{\pgf@xa}{\pgf@yb}}
    \pgfpathclose
    \pgfpathmoveto{\pgfqpoint{\pgf@xb}{\pgf@ya}}
    \pgfpathlineto{\pgfpointadd{\pgfpoint{\pgf@xb}{\pgf@ya}}{\ppd@offset}}
    \pgfpathlineto{\pgfpointadd{\pgfpoint{\pgf@xb}{\pgf@yb}}{\ppd@offset}}
    \pgfpathlineto{\pgfpointadd{\pgfpoint{\pgf@xa}{\pgf@yb}}{\ppd@offset}}
    \pgfpathlineto{\pgfqpoint{\pgf@xa}{\pgf@yb}}
    \pgfpathmoveto{\pgfqpoint{\pgf@xb}{\pgf@yb}}
    \pgfpathlineto{\pgfpointadd{\pgfpoint{\pgf@xb}{\pgf@yb}}{\ppd@offset}}
  }
}
\makeatother

\tikzset{l3 switch/.style={
    parallelepiped,fill=switch, draw=white,
    minimum width=0.75cm,
    minimum height=0.75cm,
    parallelepiped offset x=1.75mm,
    parallelepiped offset y=1.25mm,
    path picture={
      \node[fill=white,
        circle,
        minimum size=6pt,
        inner sep=0pt,
        append after command={
          \pgfextra{
            \foreach \angle in {0,45,...,360}
            \draw[-latex,fill=white] (\tikzlastnode.\angle)--++(\angle:2.25mm);
          }
        }
      ] 
       at ([xshift=-0.75mm,yshift=-0.5mm]path picture bounding box.center){};
    }
  },
  ports/.style={
    line width=0.3pt,
    top color=gray!20,
    bottom color=gray!80
  },
  rack switch/.style={
    parallelepiped,fill=white, draw,
    minimum width=1.25cm,
    minimum height=0.25cm,
    parallelepiped offset x=2mm,
    parallelepiped offset y=1.25mm,
    xscale=-1,
    path picture={
      \draw[top color=gray!5,bottom color=gray!40]
      (path picture bounding box.south west) rectangle 
      (path picture bounding box.north east);
      \coordinate (A-west) at ([xshift=-0.2cm]path picture bounding box.west);
      \coordinate (A-center) at ($(path picture bounding box.center)!0!(path picture bounding box.south)$);
      \foreach \x in {0.275,0.525,0.775}{
        \draw[ports]([yshift=-0.05cm]$(A-west)!\x!(A-center)$) rectangle +(0.1,0.05);
        \draw[ports]([yshift=-0.125cm]$(A-west)!\x!(A-center)$) rectangle +(0.1,0.05);
       } 
      \coordinate (A-east) at (path picture bounding box.east);
      \foreach \x in {0.085,0.21,0.335,0.455,0.635,0.755,0.875,1}{
        \draw[ports]([yshift=-0.1125cm]$(A-east)!\x!(A-center)$) rectangle +(0.05,0.1);       
      }
    }
  },
  server/.style={
    parallelepiped,
    fill=white, draw,
    minimum width=0.35cm,
    minimum height=0.75cm,
    parallelepiped offset x=3mm,
    parallelepiped offset y=2mm,
    xscale=-1,
    path picture={
      \draw[top color=gray!5,bottom color=gray!40]
      (path picture bounding box.south west) rectangle 
      (path picture bounding box.north east);
      \coordinate (A-center) at ($(path picture bounding box.center)!0!(path picture bounding box.south)$);
      \coordinate (A-west) at ([xshift=-0.575cm]path picture bounding box.west);
      \draw[ports]([yshift=0.1cm]$(A-west)!0!(A-center)$) rectangle +(0.2,0.065);
      \draw[ports]([yshift=0.01cm]$(A-west)!0.085!(A-center)$) rectangle +(0.15,0.05);
      \fill[black]([yshift=-0.35cm]$(A-west)!-0.1!(A-center)$) rectangle +(0.235,0.0175);
      \fill[black]([yshift=-0.385cm]$(A-west)!-0.1!(A-center)$) rectangle +(0.235,0.0175);
      \fill[black]([yshift=-0.42cm]$(A-west)!-0.1!(A-center)$) rectangle +(0.235,0.0175);
    }  
  },
}

\usetikzlibrary{calc, shadings, shadows, shapes.arrows}

% Styles for interfaces and edge labels
\tikzset{%
  interface/.style={draw, rectangle, rounded corners, font=\LARGE\sffamily},
  ethernet/.style={interface, fill=yellow!50},% ethernet interface
  serial/.style={interface, fill=green!70},% serial interface
  speed/.style={sloped, anchor=south, font=\large\sffamily},% line speed at edge
  route/.style={draw, shape=single arrow, single arrow head extend=4mm,
    minimum height=1.7cm, minimum width=3mm, white, fill=switch!20,
    drop shadow={opacity=.8, fill=switch}, font=\tiny}% inroute / outroute arrows
}
\newcommand*{\shift}{1.3cm}% For placing the arrows later

% The router icon
\newcommand*{\router}[1]{
\begin{tikzpicture}    
  \coordinate (ll) at (-3,0.5);
  \coordinate (lr) at (3,0.5);
  \coordinate (ul) at (-3,2);
  \coordinate (ur) at (3,2);
  \shade [shading angle=90, left color=switch, right color=white] (ll)
    arc (-180:-60:3cm and .75cm) -- +(0,1.5) arc (-60:-180:3cm and .75cm)
    -- cycle;
  \shade [shading angle=270, right color=switch, left color=white!50] (lr)
    arc (0:-60:3cm and .75cm) -- +(0,1.5) arc (-60:0:3cm and .75cm) -- cycle;
  \draw [thick] (ll) arc (-180:0:3cm and .75cm) -- (ur) arc (0:-180:3cm and .75cm)
    -- cycle;
  \draw [thick, shade, upper left=switch, lower left=switch,
    upper right=switch, lower right=white] (ul)
    arc (-180:180:3cm and .75cm);
  \node at (0,0.5){\color{blue!60!black}\Huge #1};% The name of the router
  % The four arrows, symbols for incoming and outgoing routes:
  \begin{scope}[yshift=2cm, yscale=0.28, transform shape]
    \node[route, rotate=45, xshift=\shift] {\strut};
    \node[route, rotate=-45, xshift=-\shift] {\strut};
    \node[route, rotate=-135, xshift=\shift] {\strut};
    \node[route, rotate=135, xshift=-\shift] {\strut};
  \end{scope}
\end{tikzpicture}}

\makeatletter
\pgfdeclareradialshading[tikz@ball]{cloud}{\pgfpoint{-0.275cm}{0.4cm}}{%
  color(0cm)=(tikz@ball!75!white);
  color(0.1cm)=(tikz@ball!85!white); 
  color(0.2cm)=(tikz@ball!95!white); 
  color(0.7cm)=(tikz@ball!89!black); 
  color(1cm)=(tikz@ball!75!black)
}
\tikzoption{cloud color}{\pgfutil@colorlet{tikz@ball}{#1}\def\tikz@shading{cloud}\tikz@addmode{\tikz@mode@shadetrue}}
\makeatother

\tikzset{my cloud/.style={
     cloud, draw, aspect=2,
     cloud color={gray!5!white}
  }
}

\begin{document}

\begin{tikzpicture}

\node[server](server 1){};
\node[server, right of= server 1](server 2){};
\node[server, right of= server 2](server 3){};

\node[rack switch, above of=server 2,xshift=0.1cm,yshift=0.3cm](rack switch 1){};

\draw[thick,darkgray!10!gray] (server 1.north)--(rack switch 1);
\draw[thick,darkgray!10!gray] (server 2.north)--(rack switch 1);
\draw[thick,darkgray!10!gray] (server 3.north)--(rack switch 1);

\begin{scope}[xshift=3.5cm]
\node[server](server 4){};
\node[server, right of= server 4](server 5){};
\node[server, right of= server 5](server 6){};

\node[rack switch, above of=server 5,xshift=0.1cm,yshift=0.3cm](rack switch 2){};

\draw[thick,darkgray!10!gray] (server 4.north)--(rack switch 2);
\draw[thick,darkgray!10!gray] (server 5.north)--(rack switch 2);
\draw[thick,darkgray!10!gray] (server 6.north)--(rack switch 2);
\end{scope}

\begin{scope}[xshift=8cm]
\node[server](server 7){};
\node[server, right of= server 7](server 8){};
\node[server, right of= server 8](server 9){};

\node[rack switch, above of=server 8,xshift=0.1cm,yshift=0.3cm](rack switch 3){};

\draw[thick,darkgray!10!gray] (server 7.north)--(rack switch 3);
\draw[thick,darkgray!10!gray] (server 8.north)--(rack switch 3);
\draw[thick,darkgray!10!gray] (server 9.north)--(rack switch 3);
\end{scope}


\node[l3 switch, above of =rack switch 1, xshift=1.5cm,yshift=0.5cm](l3 switch 1){};
\node[l3 switch, above of =rack switch 2, xshift=2cm,yshift=0.5cm](l3 switch 2){};

\begin{scope}[very thick,darkgray!10!gray]
\draw ($(rack switch 1.north)!0.5!(rack switch 1.north west)$)--
 ($(l3 switch 2.south)!0.5!(l3 switch 2.south west)$);
\draw ($(rack switch 1.north)!0.5!(rack switch 1.north east)$)--
 ($(l3 switch 1.south)!0.5!(l3 switch 1.south west)$);

\draw ($(rack switch 2.north)!0.5!(rack switch 2.north west)$)--
 ($(l3 switch 2.south)!0!(l3 switch 2.south west)$);
\draw ($(rack switch 2.north)!0.5!(rack switch 2.north east)$)--
 ($(l3 switch 1.south)!0!(l3 switch 1.south west)$);  

\draw ($(rack switch 3.north)!0.5!(rack switch 3.north west)$)--
 ($(l3 switch 2.south)!0.5!(l3 switch 2.south east)$);
\draw ($(rack switch 3.north)!0.5!(rack switch 3.north east)$)--
 ($(l3 switch 1.south)!0.5!(l3 switch 1.south east)$); 

\draw ($(l3 switch 2.north west)!0.25!(l3 switch 2.south west)$)--
($(l3 switch 1.north east)!0.25!(l3 switch 1.south east)$)
;
\draw ($(l3 switch 2.north west)!0.75!(l3 switch 2.south west)$)--
($(l3 switch 1.north east)!0.75!(l3 switch 1.south east)$)
;

\end{scope} 

\node[l3 switch, above of =l3 switch 1, xshift=2cm,yshift=0.75cm](border 1){}; 

% = = = = = = = = = = = = = = = =
% Labels
% = = = = = = = = = = = = = = = =


\node[xshift=-1.05cm,yshift=0.2cm,left of = server 3,align=left] (lev1) {Computing Servers};

\node[xshift=0.9cm,yshift=0.3cm,above of = lev1,align=left](lev2) {Access Layer};

\node[xshift=1.6cm,yshift=0.4cm,above of = lev2,align=left](lev3) {Aggregation Layer};
\node[xshift=2.55cm,yshift=0.75cm,above of = lev3,align=right](lev4) {Core Layer};
\node[xshift=5.7cm,yshift=1.2cm,above of = lev4,align=right](lev5) {Gateway Router};

% = = = = = = = = = = = = = = = =
% Shifted part
% = = = = = = = = = = = = = = = =

\begin{scope}[xshift=12cm]
\node[server](server 1-a){};
\node[server, right of= server 1-a](server 2-a){};
\node[server, right of= server 2-a](server 3-a){};

\node[rack switch, above of=server 2-a,xshift=0.1cm,yshift=0.3cm](rack switch 1-a){};

\draw[thick,darkgray!10!gray] (server 1-a.north)--(rack switch 1-a);
\draw[thick,darkgray!10!gray] (server 2-a.north)--(rack switch 1-a);
\draw[thick,darkgray!10!gray] (server 3-a.north)--(rack switch 1-a);

\begin{scope}[xshift=3.5cm]
\node[server](server 4-a){};
\node[server, right of= server 4-a](server 5-a){};
\node[server, right of= server 5-a](server 6-a){};

\node[rack switch, above of=server 5-a,xshift=0.1cm,yshift=0.3cm](rack switch 2-a){};

\draw[thick,darkgray!10!gray] (server 4-a.north)--(rack switch 2-a);
\draw[thick,darkgray!10!gray] (server 5-a.north)--(rack switch 2-a);
\draw[thick,darkgray!10!gray] (server 6-a.north)--(rack switch 2-a);
\end{scope}

\begin{scope}[xshift=8cm]
\node[server](server 7-a){};
\node[server, right of= server 7-a](server 8-a){};
\node[server, right of= server 8-a](server 9-a){};

\node[rack switch, above of=server 8-a,xshift=0.1cm,yshift=0.3cm](rack switch 3-a){};

\draw[thick,darkgray!10!gray] (server 7-a.north)--(rack switch 3-a);
\draw[thick,darkgray!10!gray] (server 8-a.north)--(rack switch 3-a);
\draw[thick,darkgray!10!gray] (server 9-a.north)--(rack switch 3-a);
\end{scope}


\node[l3 switch, above of =rack switch 1-a, xshift=1.5cm,yshift=0.5cm](l3 switch 1-a){};
\node[l3 switch, above of =rack switch 2-a, xshift=2cm,yshift=0.5cm](l3 switch 2-a){};

\begin{scope}[very thick,darkgray!10!gray]
\draw ($(rack switch 1-a.north)!0.5!(rack switch 1-a.north west)$)--
 ($(l3 switch 2-a.south)!0.5!(l3 switch 2-a.south west)$);
\draw ($(rack switch 1-a.north)!0.5!(rack switch 1-a.north east)$)--
 ($(l3 switch 1-a.south)!0.5!(l3 switch 1-a.south west)$);

\draw ($(rack switch 2-a.north)!0.5!(rack switch 2-a.north west)$)--
 ($(l3 switch 2-a.south)!0!(l3 switch 2-a.south west)$);
\draw ($(rack switch 2-a.north)!0.5!(rack switch 2-a.north east)$)--
 ($(l3 switch 1-a.south)!0!(l3 switch 1-a.south west)$);  

\draw ($(rack switch 3-a.north)!0.5!(rack switch 3-a.north west)$)--
 ($(l3 switch 2-a.south)!0.5!(l3 switch 2-a.south east)$);
\draw ($(rack switch 3-a.north)!0.5!(rack switch 3-a.north east)$)--
 ($(l3 switch 1-a.south)!0.5!(l3 switch 1-a.south east)$); 

\draw ($(l3 switch 2-a.north west)!0.25!(l3 switch 2-a.south west)$)--
($(l3 switch 1-a.north east)!0.25!(l3 switch 1-a.south east)$)
;
\draw ($(l3 switch 2-a.north west)!0.75!(l3 switch 2-a.south west)$)--
($(l3 switch 1-a.north east)!0.75!(l3 switch 1-a.south east)$)
;

\end{scope} 

\node[l3 switch, above of =l3 switch 1-a, xshift=2cm,yshift=0.75cm](border 1-a){}; 

\begin{scope}[very thick,darkgray!10!gray]
\draw ($(border 1-a.south)!0.5!(border 1-a.south west)$)--
 (l3 switch 1-a.north);

\draw[thick] (border 1-a.south)--
 ([xshift=0.1cm]l3 switch 1.north);

\draw ($(border 1-a.south)!-0.5!(border 1-a.south west)$)--
 (l3 switch 2-a.north);

\draw[thick] (border 1-a.south)--
 ([xshift=0.05cm]l3 switch 2.north); 
\end{scope}
\end{scope}


% = = = = = = = = = = = = = = = =
% Background rectangle - removed
% = = = = = = = = = = = = = = = =

\path ($(server 3.south west)!0.9!(lev1.south east)-(0,0.4cm)$) coordinate (A)--
([yshift=0.86cm]A |- lev4.north east)coordinate (B)--
($(B)+(11.2cm,0)$)coordinate (C);

% = = = = = = = = = = = = = = = =
% Border Router and Internet
% = = = = = = = = = = = = = = = =

% interconnections of border 1
\begin{scope}[very thick,darkgray!10!gray]
\draw ($(border 1.south)!0.5!(border 1.south west)$)--
 (l3 switch 1.north);

\draw[thick] (border 1.south)--
 ([xshift=-0.05cm]l3 switch 1-a.north);

\draw ($(border 1.south)!-0.5!(border 1.south west)$)--
 (l3 switch 2.north);

\draw[thick] (border 1.south)--
 ([xshift=-0.1cm]l3 switch 2-a.north);
\end{scope}

\begin{scope}
\node[yshift=1cm,scale=0.2] (brouter) at (C) {\router{}}
edge[very thick,darkgray!10!gray] ([xshift=0.1cm,yshift=0.5cm]border 1);

\node[yshift=0.65cm,my cloud, minimum width=1.25cm, minimum height=1.55cm, above of=brouter,font=\large] (it)  {Internet} edge[very thick,darkgray!30!gray] (brouter);
\draw[very thick,darkgray!30!gray](brouter)--([xshift=0.1cm,yshift=0.125cm]border 1-a.north);
\end{scope}

% = = = = = = = = = = = = = = = =
% paths
% = = = = = = = = = = = = = = = =

% legend
\begin{customlegend}[
legend entries={
North-South path,
East-West path
},
legend cell align=left,
legend style={at={([xshift=10.375cm,yshift=0.75cm]it.east)},font=\small}]
\addlegendimage{stealth-stealth,very thick,red!80!black}
\addlegendimage{stealth-stealth,very thick,green!70!black}
\end{customlegend}

% paths: north-south
\draw[stealth-stealth,very thick, red!80!black,shorten <=0.025cm, shorten >=0.56cm]([yshift=-0.25cm]brouter.west)--([xshift=0.05cm]border 1.north);

\draw[stealth-stealth,very thick, red!80!black,shorten <=0.05cm, shorten >=0.125cm](border 1.south)--([yshift=0.075cm,xshift=0.4cm]l3 switch 1.north);

\draw[stealth-stealth,very thick, red!80!black,shorten <=0.1cm, shorten >=0.2cm]([xshift=-0.15cm]l3 switch 1.south)--([yshift=0.075cm,xshift=-0.65cm]rack switch 2.north);

\draw[stealth-stealth,very thick, red!80!black,shorten <=0.1cm, shorten >=0.1cm]([xshift=-0.25cm]rack switch 2.south)--([yshift=0.075cm,xshift=-0.06cm]server 6.north);

% paths: east-west
\draw[stealth-stealth,very thick, green!70!black,shorten <=0.1cm, shorten >=0.1cm]([xshift=-0.25cm]rack switch 1-a.south)--([yshift=0.075cm,xshift=-0.06cm]server 3-a.north);

\draw[stealth-stealth,very thick, green!70!black,shorten <=0.025cm, shorten >=0.2cm]([xshift=-0.4cm]l3 switch 1-a.south)--([yshift=0.075cm,xshift=-0.4cm]rack switch 1-a.north);

\draw[stealth-stealth, very thick, green!70!black,shorten <=0.1cm, shorten >=0.2cm]([xshift=-0.15cm]l3 switch 1-a.south)--([yshift=0.075cm,xshift=-0.65cm]rack switch 2-a.north);

\draw[stealth-stealth,very thick, green!70!black,shorten <=0.1cm, shorten >=0.15cm]([xshift=-0.1cm]rack switch 2-a.south)--([yshift=0.075cm,xshift=-0.12cm]server 5-a.north);

\end{tikzpicture}

\end{document}

Answer 19

Here is a picture intended to explain the disk method for computing the volume of a solid of revolution. I originally created it for my calculus class; I later redrew it to use as the central example in my still-unfinished Asymptote tutorial. Consequently, the code is fairly mature.

It is, of course, drawn using Asymptote.

The source code:

//Function to return a brace path
real innerangle = radians(60);
real outerangle = radians(70);
real midangle = radians(0);
path brace(pair a, pair b, real amplitude = .14*length(b-a)) {
  transform t = identity();
  real length = length(b-a);
  real sign = 1;
  if (amplitude < 0) {
    //    amplitude *= -1;
    sign = -1;
  }
  path brace = (0,0){expi(sign*outerangle)} :: {expi(sign*midangle)}(length/4, amplitude/2)
          :: {expi(sign*innerangle)} (length/2, amplitude) {expi(-sign*innerangle)}
  :: {expi(-sign*midangle)}(3*length/4, amplitude/2) :: {expi(-sign*outerangle)} (length,0);
  real angle = degrees(atan2((b-a).y, (b-a).x));
  t = rotate(angle)*t;
  t = shift(a) * t;
  return t * brace;
}

//Define the command drawshifted, to be used later
void drawshifted(path g, pair trueshift, picture pic = currentpicture, Label label="", pen pen=currentpen, arrowbar arrow=None, arrowbar bar=None, margin margin=NoMargin, marker marker=nomarker)
{
  picture opic;
  draw(opic, L=label, g, p=pen, arrow=arrow, bar=bar, margin=margin, marker=marker);

  pic.add(new void(frame f, transform t) {
      add(f,opic.fit(shift(trueshift)*t));
    });
  pic.addBox(min(opic), max(opic), trueshift, trueshift);
}

usepackage("amsmath");

real yellowPart = 0.2;
real unit = 2cm;
real truecm = cm / unit;
unitsize(unit);
pen backgroundpen = yellowPart*yellow + (1-yellowPart)*white;
frame finish() {
  currentlight.background = backgroundpen;
  frame toreturn = bbox(backgroundpen, Fill);
  currentpicture = new picture;
  unitsize(unit);
  return toreturn;
}

/*------------------------------*/

//Basic settings
settings.outformat="pdf";
defaultpen(fontsize(10pt));
import graph;

//Save some important numbers.
real xmin = -0.1;
real xmax = 2;
real ymin = -0.1;
real ymax = 2;

//Draw the graph and fill the area under it.
real f(real x) { return sqrt(x); }
path s = graph(f, 0, 2, operator..);
path fillregion = s -- (xmax,0) -- cycle;
pen fillpen = mediumgray;
fill(fillregion, fillpen);
draw(s, L=Label("$y=f(x)$", position=EndPoint));

//Fill the strip of width dx
real x = 1.4;
real dx = .05;
real t0 = times(s,x)[0];
real t1 = times(s,x+dx)[0];
path striptop = subpath(s,t0,t1);
filldraw((x,0) -- striptop -- (x+dx,0) --  cycle, black);

//Draw the bars labeling the width dx
real barheight = f(x+dx);
pair barshifty = (0, 0.2cm);
Label dxlabel = Label("$dx$", position=MidPoint, align=2N);
drawshifted((x,barheight) -- (x+dx, barheight), trueshift=barshifty, label=dxlabel, bar=Bars);

//Draw the arrows pointing inward toward the dx label
real myarrowlength = 0.3cm;
margin arrowmargin = DotMargin;
path leftarrow = shift(barshifty) * ((-myarrowlength, 0) -- (0,0));
path rightarrow = shift(barshifty) * ((myarrowlength, 0) -- (0,0));
draw((x, barheight), leftarrow, arrow=Arrow(), margin=arrowmargin);
draw((x+dx, barheight), rightarrow, arrow=Arrow(), margin=arrowmargin);

//Draw the bar labeling the height f(x)
real barx = x + dx;
pair barshiftx = (0.42cm, 0);
Label fxlabel = Label("$f(x)$", align=(0,0), position=MidPoint, filltype=Fill(fillpen));
drawshifted((barx,0) -- (barx, f(x)), trueshift=barshiftx, label=fxlabel, arrow=Arrows(), bar=Bars); 

//Draw the axes on top of everything that has gone before
arrowbar axisarrow = Arrow(TeXHead);
Label xlabel = Label("$x$", position=EndPoint);
draw((xmin,0) -- (xmax,0), arrow=axisarrow, L=xlabel);
Label ylabel = Label("$y$", position=EndPoint);
draw((0,ymin) -- (0,ymax), arrow = axisarrow, L=ylabel);

//Draw the tick mark on the x-axis
path tick = (0,0) -- (0,-0.15cm);
Label ticklabel = Label("$x$", position=EndPoint);
draw((x,0), tick, L=ticklabel);

frame pic2dFrame = finish();

/* ----------------------------------------------------- */

settings.prc = false;
settings.render=8;
import three;

currentprojection = orthographic(5,0,10, up=Y);
//currentprojection=oblique;
//currentprojection=perspective(6,0,10,up=Y);

pen color = white;
material surfacepen = material(diffusepen=color+opacity(1.0), emissivepen=0.2*color);
material planepen = material(diffusepen=opacity(0.6), emissivepen=0.8*color);
pen diskpen = black+opacity(1.0);

path3 p3 = path3(s);
draw(p3);

surface FilledRegion = surface(fillregion);
draw(FilledRegion, surfacepen = gray(0.6) + opacity(0.8));

surface solidsurface = surface(p3, c=O, axis=X);
draw(solidsurface, surfacepen=surfacepen);

/*
int n = length(p3);
for (real i = 0; i <= n; i += n/10) {
  if (i >= n) i -= .01;
  draw(solidsurface.vequals(i), gray(0.3));
}
*/
draw(solidsurface.vequals(length(p3) - .001), gray(0.3));

real extra = 0.4 truecm;
path planeboundary = (xmin,ymin) -- (xmax+extra,ymin) -- (xmax+extra,ymax+extra) -- (xmin,ymax+extra) -- cycle;
path planeoutside = planeboundary -- fillregion -- cycle;
draw(surface(planeoutside), surfacepen=planepen);

transform pushoutside = shift(0,.001);
striptop = pushoutside*striptop;
path3 dVtop = path3(striptop);
path3 openStrip = (x,0,0) -- dVtop -- (x+dx,0,0);
surface disk = surface(openStrip, c=O, axis=X);
draw(disk, diskpen);

triple cameraDirection(triple pt, projection P = currentprojection) {
  if (P.infinity) {
    return unit(P.camera);
  } else {
    return unit(P.camera - pt);
  }
}

triple towardCamera(triple pt, real dist = 1 truecm, projection P = currentprojection) {
  return pt + dist*cameraDirection(pt, P);
}

draw(xmin*X -- xmax*X, arrow=Arrow3(TeXHead2(normal=Z)));
draw(ymin*Y -- ymax*Y, arrow=Arrow3(TeXHead2(normal=Z)));
label("$x$", position=towardCamera(xmax*X), align = E);
label("$y$", position=towardCamera(ymax*Y), align=N);

frame pic3dFrame = finish();

/* ----------------------------------------------------------------- */

currentprojection=orthographic((3,0,10), up=Y);

diskpen = mediumgray;
draw(disk, diskpen);

transform3 T = rotate(10, X);
path3 brace = T*path3(brace((x+dx,barheight), (x+dx,0)));
draw(brace--cycle);
label("$r=f(x)$", position=midpoint(brace), align=E);

//Draw the bars labeling the width dx
path3 dxlabelpath = T * ((x, barheight, 0) -- (x+dx, barheight, 0));
draw(dxlabelpath, L=dxlabel, Bars3);

arrow(relpoint(dxlabelpath,0), dir=W, length=myarrowlength, margin=DotMargin3, arrow=Arrow3(emissive(black)));
arrow(relpoint(dxlabelpath,1), dir=E, length=myarrowlength, margin=DotMargin3, arrow=Arrow3(emissive(black)));

draw(xmin*X -- xmax*X, arrow=Arrow3(TeXHead2(normal=Z)));
draw(ymin*Y -- ymax*Y, arrow=Arrow3(TeXHead2(normal=Z)));
label("$x$", position=towardCamera(xmax*X), align = E);
label("$y$", position=towardCamera(ymax*Y), align=N);

frame oneSlice = finish();
/* ----------------------------------------------------------------- */

label(minipage("\raggedright Dimensions of infinitesimally thin sheet: 
\begin{description}
\item[Area:] $\pi r^2 = \pi [f(x)]^2$
\item[Thickness:] $dx$
\item[Volume:] $dV = \text{Area}\cdot\text{thickness} = \pi [f(x)]^2\;dx$
\end{description}"
,6cm));

frame labelFrame = finish();

/* ----------------------------------------------------------------- */

unit = 1;
unitsize(unit);
add(pic3dFrame);
add(labelFrame, position=(max(pic3dFrame).x, min(pic3dFrame).y - 1cm), align=SW);
pic3dFrame = finish();

/* ----------------------------------------------------------------- */

//unitsize(1);    // Set the usual (postscript) coordinates.
add(pic2dFrame);
add(pic3dFrame, position=max(pic2dFrame), align=SE);
add(oneSlice, position=min(pic2dFrame)+(0,-1cm), align=SE);

// Scale up by 4 in order to increase resolution.
shipout(scale(4)*finish());

Answer 20

Visualisation of the Poincaré disk model:

\documentclass[a4paper,fleqn,papersize]{jsarticle}
\usepackage{graphicx}
\usepackage{MePoTeX}
\usepackage{amsmath,amssymb}
\usepackage{mtcastle}
\usepackage{ascmac}
\usepackage{eclarith,qbgraph}
\setlength{\columnseprule}{0.2pt}
\setlength{\textwidth}{190truemm}
\setlength{\textheight}{257truemm}
\setlength{\oddsidemargin}{-15truemm}
\setlength{\topmargin}{-15truemm}
\setlength{\headheight}{0mm}
\setlength{\headsep}{0mm}
\setlength{\fboxrule}{0.2pt}
%------------------------------------------------------------------------
\title{Poincare Disc}
\author{Moonlight Satie}
\begin{document}
%------------------------------------------------------------------------
\maketitle
%------------------------------------------------------------------------
%------------------------------------------------------------------------
\hspace{-4mm}
\begin{MPpic}<96mm>(2,2)(-1,-1)%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
\sendMP{%================================================================
fill fullcircle scaled 2w withcolor 0.5white;
draw fullcircle scaled 2w;
numeric m,n;
m:=4;n:=5;
%-------------------------------------------------------------------
numeric ta,tb,ca,sa,cb,sb,cab,sab,tmpa,tmpb,k;
ta:=180/m;tb:=180/n;
ca:=cosd(ta);sa:=sind(ta);cb:=cosd(tb);sb:=sind(tb);
sab:=sa*cb+ca*sb;cab:=ca*cb-sa*sb;
tmpa:=(sb+sa/cab)/sab;tmpb:=sa/cab;
k:=1/(tmpa+-+tmpb);
}%=======================================================================
\sendMP{%================================================================
def poiP(expr p,r,x)=%----------------------------------------------
p+(x-p)/length(x-p)/length(x-p)*r*r;
enddef;%------------------------------------------------------------
def fidraw(expr p,c)=%----------------------------------------------
fill p scaled w withcolor c;
draw p scaled w;
enddef;%------------------------------------------------------------
def centPoiT(expr X,Y,Z)=%----------------------------------------------
if abs(angle(X)-angle(Y))>1:
whatever[(X+Y)/2,(X+Y)/2+(X-Y) rotated 90]=%
whatever[(X+Z)/2,(X+Z)/2+(X-Z) rotated 90];%
else:(0,0);fi;
enddef;%------------------------------------------------------------
def centPoi(expr X,Y)=%----------------------------------------------
if X=(0,0):(0,0);
elseif Y=(0,0):(0,0);
else:centPoiT(X,Y,X/(length(X)**2));fi;
enddef;%------------------------------------------------------------
def angleChk(expr X,Y)=%-------------------------------------------------
if angle(X)<angle(Y):true;else:false;fi;
enddef;%------------------------------------------------------------
def arcPoi(expr X,Y,R)=%----------------------------------------------
if length(R)<1:X--Y;
elseif X=O:X--Y;
elseif Y=O:X--Y;
elseif angle(X)<angle(Y):
if angle(Y)-angle(X)<180:X{dir (angle(X-R)-90)}..{dir (angle(Y-R)-90)}Y;
else:X{dir (angle(X-R)+90)}..{dir (angle(Y-R)+90)}Y;fi;
else:if angle(X)-angle(Y)>180:X{dir (angle(X-R)-90)}..{dir (angle(Y-R)-90)}Y;
else:X{dir (angle(X-R)+90)}..{dir (angle(Y-R)+90)}Y;fi;fi;
enddef;%------------------------------------------------------------
def drawPoiT(expr P,T,O,cr,cg,cb)=%------------------------------------
save Y;path q,r,s,pp;pair Y;
Y:=centPoi(P,T);q:=arcPoi(P,T,Y);
Y:=centPoi(T,O);r:=arcPoi(T,O,Y);
Y:=centPoi(O,P);s:=arcPoi(O,P,Y);
%Y:=centPoi(Q,P);p:=arcPoi(Q,P,Y);
pp:=q..r..s..cycle;
for i:=0 upto 3:fill pp rotated (90*i) scaled w withcolor (cr,cg,cb);endfor;
enddef;%------------------------------------------------------------
def drawPoiTT(expr P,T,O,cr,cg,cb)=%----------------------------------------------
save Y;path q,r,s,pp;pair Y;
Y:=centPoi(P,T);q:=arcPoi(P,T,Y);
Y:=centPoi(T,O);r:=arcPoi(T,O,Y);
Y:=centPoi(O,P);s:=arcPoi(O,P,Y);
%Y:=centPoi(Q,P);p:=arcPoi(Q,P,Y);
pp:=q..r..s..cycle;
fill pp scaled w withcolor (cr,cg,cb);
enddef;%------------------------------------------------------------
%
pair R,XX;path pop[],trip;
%
vardef nxtPoi(expr P,Q,R,S,O,n,nr,nl)=%--------------------------------
save T,U,V,X;pair T,U,V,X;
X:=centPoi(P,Q);T:=poiP(X,length(P-X),S);
U:=poiP(X,length(P-X),R);V:=poiP(X,length(P-X),O);
if length(T)<1:
if length(U)<1:
if length(P-U)>=length(P-T):
if length(Q-T)>=length(Q-U):
drawPoiT(P,T,V,0.3,0.5,0.7);drawPoiT(U,Q,V,0.1,0.3,0.5);
drawPoiT(T,U,V,0.9,0.7,0.5);drawPoiT(Q,P,V,0.7,0.5,0.3);
if n>1:
if min(length(T-P),length(T-P))>0.0001:if nr>0:
nxtPoi(P,T,U,Q,V,n-1,nr-1,nl);fi;fi;
if min(length(T-U),length(T-U))>0.0001:nxtPoi(T,U,Q,P,V,n-1,nr,nl);fi;
if min(length(Q-U),length(Q-U))>0.0001:if nl>0:
nxtPoi(U,Q,P,T,V,n-1,nr,nl-1);fi;fi;
fi;
fi;fi;fi;fi;
enddef;%------------------------------------------------------------
}%=======================================================================
\sendMP{%================================================================
pair O,A,B,C,D,E;O:=(0,0);
A:=(k,0) rotated 45;B:=A rotated 2ta;C:=B rotated 2ta;D:=C rotated 2ta;
drawPoiTT(A,B,O,0.3,0.5,0.7);drawPoiTT(C,D,O,0.1,0.3,0.5);
drawPoiTT(B,C,O,0.9,0.7,0.5);drawPoiTT(D,A,O,0.9,0.7,0.5);
%
nxtPoi(A,B,C,D,O,12,n-3,n-3);
}%=======================================================================
\end{MPpic}%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
\hfill~
%
%------------------------------------------------------------------------
\end{document}

Answer 21

When I was [for]playing with theory of envelopes, I made several drawings with lualatex anad tikz. Lualatex solely because I'm not comfortable with programming in tikz. Here is one of my favorites, Lemniscate envelope:

\documentclass{article}
\usepackage[margin=0cm,a4paper,landscape]{geometry}
\usepackage{luacode}
\usepackage{pgfplots}
\usepackage{float}

\begin{document}
    \input{lua_functions}
    \input{tikz_plot}
\end{document}

and two tex files used:

% functions.tex
\begin{luacode*}
function getCenterRadius(t)
    a = 1;
    b = 1;
    h = 0;
    k = 0;
    cX = a*(1/math.cos(t)) + h;
    cY = b*math.tan(t) + k;
    R = math.sqrt((cX-h)^2 + (cY-k)^2) -- Classic
    return cX, cY, R
end

function printHyperbola()
    for t=-1.56,1.56,0.02555 do
        xL,yL,RL = getCenterRadius(t)
        xR,yR,RR = getCenterRadius(3.1415+t)
        tex.sprint("\\draw[very thin] (axis cs:"..(xL)..","..(yL)..") circle("..(RL*10)..");")
        tex.sprint("\\draw[very thin] (axis cs:"..(xR)..","..(yR)..") circle("..(RR*10)..");")
    end
end
\end{luacode*}

and

% tikz_plot.tex
\begin{figure}
\centering
    \pgfplotsset{width=1\paperwidth, height=1\paperheight}
    \resizebox{\paperwidth}{!}
    {
        \begin{tikzpicture}
            \begin{axis}[xmin=-14.85, xmax=14.85, ymin=-10.5, ymax=10.5,
                % ticks=none,
                hide axis,
            ]
                \directlua{printHyperbola()}
            \end{axis}
        \end{tikzpicture}
    }
\end{figure}

Finally the aforementioned envelope:

This envelope is generated by sweeping a circle has its center on a hyperbola. To read more, check here.

Answer 22

The following figure is one of my favorites. The goal of the image is to explain the definition of the derivative, in the form that "f'(x_0) = m if within sufficiently small neighborhoods of x_0, f can be contained in arbitrarily narrow cones about the line through (x_0,f(x_0)) with slope m." The figure was created in TikZ. If I were to create it now, I would use Asymptote, and it would probably contain fewer arbitrary-seeming numbers.

Note that I created this image for a handout, so it had to be grayscale.

\documentclass[tikz]{standalone}
\usetikzlibrary{decorations.pathreplacing}
\usepackage{mathtools}
\DeclarePairedDelimiter{\abs}{\lvert}{\rvert}
\renewcommand{\epsilon}{\varepsilon}
\begin{document}
\begin{tikzpicture}[xscale=8,yscale=5]
    \newcommand{\xmin}{-.4} \newcommand{\xmax}{.5}  \newcommand{\deltaX}{.65}
    \begin{scope}
        \draw[black,->] (-.6,-.7) -- (.5,-.7) node[right] {$x$};
        \draw[black,->] (-.5,-.8) -- (-.5,0.5) node[above] {$y$};

%       \useasboundingbox;

    \path[fill=black!30,draw=black!30] (-.33,-.33*1.65) --
        (-.33,-.33*.35) --
        (.33,.33*.35) -- (.33,.33*1.65) -- cycle;
    \draw[thick,densely dotted] (.33,-.72) 
        node[below] (delta3) {$x_0+\delta\strut$} -- (.33,.33*1.65);
    \draw[thick,densely dotted] (-.33,-.72) 
        node[below] (mdelta3) {$x_0-\delta\strut$} -- (-.33,-.33*.35);

    \fill[black!50] (-.25,-.25*3/2) -- (-.25,-.25/2) -- (.25,.25/2) -- 
        (.25,.25*3/2) -- cycle;

    \path[fill=black!70] (-.15,-.15*1.25) -- (-.15,-.15*.75) --
        (.15,.15*.75) -- (.15,.15*1.25) -- cycle;

    \node[circle,draw=black,inner sep=0pt,minimum size=3pt,fill=black] (x0y0) at (0,0) {};
    \draw[black,domain=\xmin:\xmax,samples=2] plot(\x,\x) 
        node[right] {$\Delta y = f'(x_0) \Delta x$};
    \draw[very thick,black,smooth,domain=\xmin:\xmax,samples=30] 
        plot (\x,{1-1/(\x+1)}) node[right] {$y=f(x)$};
    \draw[black,very thin] (x0y0) -- (0,{-.72}) node[below] (x0) {$x_0\strut$};
    \draw[black,very thin] (x0y0) -- (-.52,0) node[left]{$y_0$};

\end{scope}

\draw[decorate,decoration={brace,amplitude=5pt,mirror,raise=1pt}]
    (.33,.33*.35) -- 
    node[right]{\hspace{6pt}$\epsilon \Delta x$} (.33,.33);
\draw[decorate,decoration={brace,amplitude=5pt}] 
    (delta3.south) -- 
    node[below] {$\rule{0pt}{14pt}\abs{\Delta x} < \delta$} 
    (mdelta3.south);

\end{tikzpicture}
\end{document}

Answer 23

Thanks to this question y was able to do something I wanted to do a long time ago: the shape of pi with the digits of pi.

The only "hard" thing is the shape, but looking at the question I said it's pretty simple.

\documentclass[10pt]{article}

\usepackage{graphicx}   
\usepackage{shapepar}
\usepackage{microtype}

\def\pipar#1{\shapepar{\pishape}#1\par}
\def\pishape{%
{25.0839}%
{0.0838926}b{14.3456}\\%
{0.0838926}t{14.3456}{33.3054}\\%
{0.503356}t{11.5772}{37.6678}\\%
{1.25839}t{9.98322}{39.6812}\\%
{2.09732}t{8.52614}{41.5578}\\%
{2.85235}t{7.21477}{42.8691}\\%
{3.27181}t{6.7953}{43.2886}\\%
{4.11074}t{5.95638}{43.7081}\\%
{5.28524}t{4.78188}{43.7081}\\%
{5.62081}t{4.44631}{15.1007}st{19.547}{12.6678}st{32.2148}{15.0168}\\%
{5.62081}t{4.44631}{7.9698}t{19.547}{2.34899}t{32.2148}{2.34899}\\%
{6.04027}t{4.18011}{6.22257}t{19.4227}{2.37488}t{32.1424}{2.37047}\\%
{6.87919}t{3.64772}{5.16101}t{19.1741}{2.42667}t{31.9978}{2.41343}\\%
{7.63423}t{3.16856}{4.04621}t{18.9504}{2.47328}t{31.8676}{2.45208}\\%
{8.05369}t{2.90236}{3.80463}t{18.8261}{2.49917}t{31.7953}{2.47356}\\%
{8.38926}t{2.6894}{3.61137}t{18.7267}{2.51989}t{31.7245}{2.50373}\\%
{9.22819}t{2.15701}{3.12823}t{18.4781}{2.57167}t{31.5474}{2.57045}\\%
{9.98322}t{1.67785}{2.96021}t{18.2544}{2.61828}t{31.388}{2.6305}\\%
{11.5772}t{0.415968}{2.85584}t{17.7821}{2.71667}t{31.0515}{2.75727}\\%
{11.9966}t{0.0838926}{2.91826}t{17.6578}{2.74256}t{30.9629}{2.79063}\\%
{12.4161}t{0.0838926}{2.64861}t{17.5336}{2.76846}t{30.8743}{2.82399}\\%
{12.7517}t{0.0838926}{2.43289}t{17.4088}{2.81003}t{30.8035}{2.85068}\\%
{13.1711}t{0.0838926}{2.22315}t{17.2529}{2.862}t{30.715}{2.88404}\\%
{13.5906}t{0.0838926}{2.01342}t{17.097}{2.91397}t{30.6264}{2.9174}\\%
{14.0101}t{0.0838926}{0.838926}t{16.9411}{2.96594}t{30.5378}{2.95076}\\%
{14.0101}e{0.922819}t{16.9411}{2.96594}t{30.5378}{2.95076}\\%
{14.7651}t{16.6605}{3.05948}t{30.3785}{3.01081}\\%
{15.604}t{16.3487}{3.16342}t{30.2013}{3.18792}\\%
{16.7785}t{15.9121}{3.30893}t{30.0039}{3.3854}\\%
{21.896}t{14.0101}{3.94295}t{29.1434}{4.24586}\\%
{25.0839}t{12.7724}{4.3305}t{28.6074}{4.78188}\\%
{25.8389}t{12.4793}{4.42229}t{28.6074}{4.78188}\\%
{29.0268}t{11.2416}{4.80984}t{28.6074}{5.39494}\\%
{29.4463}t{11.0415}{4.8981}t{28.6074}{5.47561}\\%
{30.2013}t{10.6813}{5.04094}t{28.6074}{5.62081}\\%
{30.6208}t{10.4812}{5.12029}t{28.6074}{5.72383}\\%
{34.9832}t{8.40004}{5.9456}t{28.9901}{6.41263}\\%
{35.4027}t{8.19993}{6.00914}t{29.0268}{6.58557}\\%
{37.3322}t{7.27942}{6.30143}t{29.5346}{7.04256}\\%
{38.1711}t{6.87919}{6.42852}t{29.7554}{6.64702}\\%
{38.5906}t{6.87919}{6.29195}t{29.8658}{6.44925}\\%
{39.3456}t{7.09492}{5.59084}t{30.1612}{5.9965}\\%
{39.7651}t{7.21477}{5.20134}t{30.3254}{5.4129}\\%
{40.5201}t{7.63423}{4.24257}t{30.6208}{4.36242}\\%
{40.9396}t{8.01175}{3.56544}t{31.2081}{2.60067}\\%
{41.3591}t{8.38926}{2.43289}t{31.7953}{0.838926}\\%
{41.3591}e{10.8221}e{32.6342}%
}

\begin{document}

\pipar{3 . 1 4 1 5 9 2 6 5 3 5 8 9 7 9 3 2 3 8 4 6 2 6 4 3 3 8 3 2 7 9 5 0 2 8 8 4 1 9 7 1 6 9 3 9 9 3 7 5 1 0 5 8 2 0 9 7 4 9 4 4 5 9 2 3 0 7 8 1 6 4 0 6 2 8 6  2 0 8 9 9 8 6 2 8 0 3 4 8 2 5 3 4 2 1 1 7 0 6 7 9 8 2 1 4 8 0 8 6 5 1 3 2 8 2 3 0 6 6 4 7 0 9 3 8 4 4 6 0 9 5 5 0 5 8 2 2 3 1 7 2 5 3 5 9 4 0 8 1 2 8 4 8 1  1 1 7 4 5 0 2 8 4 1 0 2 7 0 1 9 3 8 5 2 1 1 0 5 5 5 9 6 4 4 6 2 2 9 4 8 9 5 4 9 3 0 3 8 1 9 6 4 4 2 8 8 1 0 9 7 5 6 6 5 9 3 3 4 4 6 1 2 8 4 7 5 6 4 8 2 3 3  7 8 6 7 8 3 1 6 5 2 7 1 2 0 1 9 0 9 1 4 5 6 4 8 5 6 6 9 2 3 4 6 0 3 4 8 6 1 0 4 5 4 3 2 6 6 4 8 2 1 3 3 9 3 6 0 7 2 6 0 2 4 9 1 4 1 2 7 3 7 2 4 5 8 7 0 0 6  6 0 6 3 1 5 5 8 8 1 7 4 8 8 1 5 2 0 9 2 0 9 6 2 8 2 9 2 5 4 0 9 1 7 1 5 3 6 4 3 6 7 8 9 2 5 9 0 3 6 0 0 1 1 3 3 0 5 3 0 5 4 8 8 2 0 4 6 6 5 2 1 3 8 4 1 4 6  9 5 1 9 4 1 5 1 1 6 0 9 4 3 3 0 5 7 2 7 0 3 6 5 7 5 9 5 9 1 9 5 3 0 9 2 1 8 6 1 1 7 3 8 1 9 3 2 6 1 1 7 9 3 1 0 5 1 1 8 5 4 8 0 7 4 4 6 2 3 7 9 9 6 2 7 4 9  5 6 7 3 5 1 8 8 5 7 5 2 7 2 4 8 9 1 2 2 7 9 3 8 1 8 3 0 1 1 9 4 9 1}

\end{document}

Answer 24

If you throw a ball at a certain angle between 0 and 90 degrees relative to the horizontal line, the trajectory of the ball is a parabolic curve. The vertical component of its velocity is changing while the horizontal one remains unchanged.

The following code has not been optimized yet.

\documentclass[pstricks,border={12pt 32pt 26pt 12pt}]{standalone}
\usepackage{pstricks-add}

\usepackage[nomessages]{fp}
\newcommand\const[3][3]{%
    \expandafter\FPeval\csname#2\endcsname{round(#3:#1)}%
    \pstVerb{/#2 \csname#2\endcsname\space def}%
}
\newcommand\Const[3][3]{\begingroup\edef\temp{\endgroup\noexpand\const[#1]{#2}{#3}}\temp}

\Const{Tpeak}{1}
\Const{Theta}{80/180*pi}
\Const{Gravity}{10}
\Const{SpeedFactor}{0.2}
\Const{FPS}{25}

\def\X#1{Vinit*cos(Theta)*#1}
\def\Y#1{Vinit*sin(Theta)*#1-Gravity*pow(2,#1)/2}

\Const{Vinit}{Tpeak*Gravity/sin(Theta)}
\Const{Xpeak}{\X{Tpeak}}
\Const{Ypeak}{\Y{Tpeak}}

\def\point#1{%
    \pnode(!Vinit Theta RadToDeg 2 copy cos mul #1 mul 3 1 roll sin mul #1 mul Gravity #1 2 exp mul 2 div sub){P}
    \pscircle[linecolor=red,fillstyle=solid,fillcolor=yellow](P){3pt}
    \pnode[!Vinit Theta RadToDeg cos mul SpeedFactor mul 0](P){PX}
    \pnode[!0 Vinit Theta RadToDeg sin mul Gravity #1 mul sub SpeedFactor mul](P){PY}
    %
    \psLine[linecolor=blue]{->}(P)(PX)
    \psLine[linecolor=magenta]{->}(P)(PX|PY)
    \psLine[linecolor=blue]{->}(P)(PY)
    %
    \uput{1.5pt}[0](PX){\tiny$V_x$}
    \FPifgt{#1}{\Tpeak}
        \uput{1.5pt}[-90](PY){\tiny$V_y$}
    \fi
    \FPiflt{#1}{\Tpeak}
        \uput[90](PY){\tiny$V_y$}
    \fi
}


\Const{DeltaTime}{1/\FPS}
\Const[0]{TotalFrames}{\FPS*2*Tpeak}
\Const[0]{TotalFrames}{TotalFrames+1}

\begin{document}
\multido{\nt=0.000+\DeltaTime}{\TotalFrames}{%
\begin{pspicture}[showgrid=false](0,-35pt)(2\dimexpr\Xpeak\psxunit\relax,\dimexpr\Ypeak\psyunit+7pt\relax)
    \parabola[linewidth=0.5\pslinewidth,linestyle=dashed](0,0)(\Xpeak,\Ypeak)
    \point{\nt}
\end{pspicture}}
\end{document}

Answer 25

For some reason I am particularly proud of this one. It was an 3D-coloured illustration for a finite-element mesh upon a spheroid (confocal to another, non-represented inner spheroid which parameters are also to be found in this program) designed for an old paper research.

It could have been done with Asymptote, which is my best tool for 3D, but for this time I wanted to stick to my favourite tool, MetaPost, so I produced that after a bit of sweat :-).

It is not particularly impressive, it was certainly crudely done (in particular I could have made use of the transparency features of Metafun, but I wasn't yet aware of them), but I have always found the result pleasant.

If called for example spheroid_mesh.mp, the drawing is to be produced with the command line mpost --mem=metafun spheroid_mesh.mp. Sorry for the old comments in French, I have not enough courage to translate them now.

verbatimtex
    %&latex
    \documentclass[12pt]{scrartcl}
    \begin{document}
etex
%
% Échelle
u := 2cm;

f = 0.1; % Porosité

beginfig(1);

% Paramètres de projection 3D (orientation du repère)
alpha = -45; % rotation de l'axe (Oy)
beta = -25; % inclinaison de l'axe (Oz)

% Sphéroïde intérieure
a1 = 0.5;
b1 = 2.5;
c = b1 +-+ a1; % Distance focale;

% Sphéroïde extérieure
const = ( sqrt(4*(c**6)*(f**2) + 27*(a1**2)*(b1**4) ) /
    (2*(3**(3/2))*f) + (a1*(b1**2))/(2*f) ) ** (1/3);
a2 = const - (c**2)/(3*const);
b2 = sqrt(a2**2 + c**2);

% Nombre de subdivision suivant la colatitude theta
ndiv = 10;

% Repère 3D projeté
pair e[];
e1 = (sind(alpha), cosd(alpha)*sind(beta)) scaled u;
e2 = (cosd(alpha),  -sind(beta)*sind(alpha)) scaled u;
e3 = (0, cosd(beta)) scaled u;

% Fonction générale de projection 3D
vardef projection (expr x, y, z) =
    x*e1 + y*e2 + z*e3
enddef;

% Variables concernant le maillage
z[0][0] = projection(0, 0, a2); % nœud supérieur

% Maillage
for i = 1 upto ndiv:
    theta[i] = i/ndiv*90;
    cote[i] = a2*cosd(theta[i]);
    r[i] = b2*sqrt(1 - (cote[i]**2)/(a2**2));
    for j = 0 upto i:
        z[i][j] =  projection(r[i]*cosd(j/i*90), r[i]*sind(j/i*90), cote[i]);
    endfor;
endfor;

% Triangles
path tr[][];
%
tr[1][1] = z[0][0] -- z[1][0] -- z[1][1] -- cycle;
for i = 2 upto ndiv:
    tr[i][1] = z[i-1][0] -- z[i][0] -- z[i][1] -- cycle;
    for j = 1 upto i-1:
        tr[i][2j] = z[i-1][j-1] -- z[i-1][j] -- z[i][j] -- cycle;
        tr[i][2j+1] = z[i-1][j] -- z[i][j] -- z[i][j+1] -- cycle;
    endfor;
endfor;

% Couleurs des triangles
cst = 0.3;
color mon_bleu, mon_rouge, mon_vert;
mon_rouge = (1, cst, cst);
mon_vert = (cst, 1, cst);
mon_bleu = (cst, cst, 1);
fill tr[1][1] withcolor mon_bleu;
for i = 2 upto ndiv:
    for j = 1 upto 2i-1:
        fill tr[i][j]  
            withcolor -i/ndiv*(j - 2i + 1)/(2i-2) * mon_rouge
                + (j-1)/(2*i-2)*i/ndiv * mon_vert 
                + (1-i/ndiv) * mon_bleu;
    endfor;
endfor;

% tracé des arêtes
for i = 1 upto ndiv:
    for j = 1 upto i:
        draw z[i][j-1] -- z[i][j];
        draw z[i-1][j-1] -- z[i][j-1];
        draw z[i-1][j-1] -- z[i][j];
    endfor; 
endfor;

% Tracé des axes du repère
pair X, Y, Z;
X = 4.75e1;
Y = 4.75e2;
Z = 3.6e3;
drawoptions(dashed evenly);
draw (origin -- projection(b2, 0, 0));
draw origin -- projection(0, b2, 0);
draw origin -- projection(0, 0, a2);
drawoptions();
drawarrow (projection(b2, 0, 0) -- X);
drawarrow (projection(0, b2, 0) -- Y);
drawarrow (projection(0, 0, a2) -- Z);

% Labels du repère
label.lft(btex $x$ etex, X);
label.rt(btex $y$ etex, Y);
label.lft(btex $z$ etex, Z);

% Pour élargissement de la bounding box 
setbounds currentpicture to boundingbox currentpicture enlarged 2bp;

endfig;
end.

Answer 26

Mandelbrot Set

Well, I didn't really come up with this, especially the coloring function. I pieced the code together from different tutorials some time ago, and now simply translatet it to Asymptote.

real iterate(pair z, pair c, int N) {
    pair zsquare = 0;

    int n = 0;

    do {
        zsquare = (z.x * z.x, z.y * z.y);
        z = (zsquare.x + zsquare.y * -1, 2 * z.x * z.y) + c;
        ++n;
    }
    while (zsquare.x + zsquare.y < 4 && n < N);

    zsquare = (z.x * z.x, z.y * z.y);
    return n - log(.5 * log(zsquare.x + zsquare.y) / log(N)) / log(2);

    return n;
}

void mandelbrot(pair size, real zoom, pair pos, int N) {
    for(int x = 0; x < size.x; ++x) {
        for(int y = 0; y < size.y; ++y) {
            pair z = (x / size.x, y / size.y) * zoom - pos;

            real res = iterate(z, z, N) / N;

            fill(box((x, y), (x + 2, y + 2)), rgb(sin(res * 4), sin(res * 5), sin(res * 6)));
        }
    }
}

mandelbrot((300, 300), 3, (2, 1.5), 128);

Answer 27

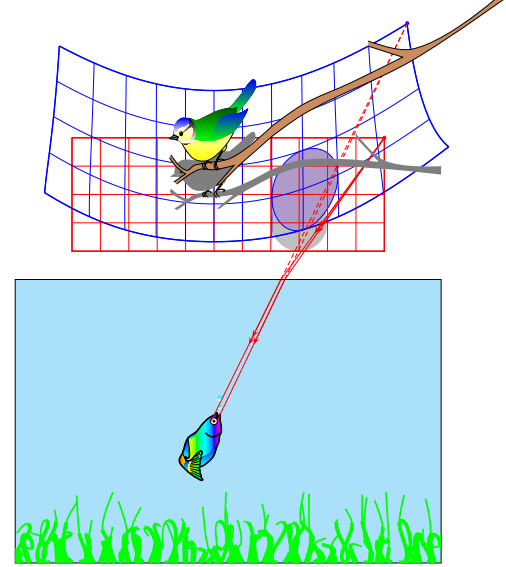
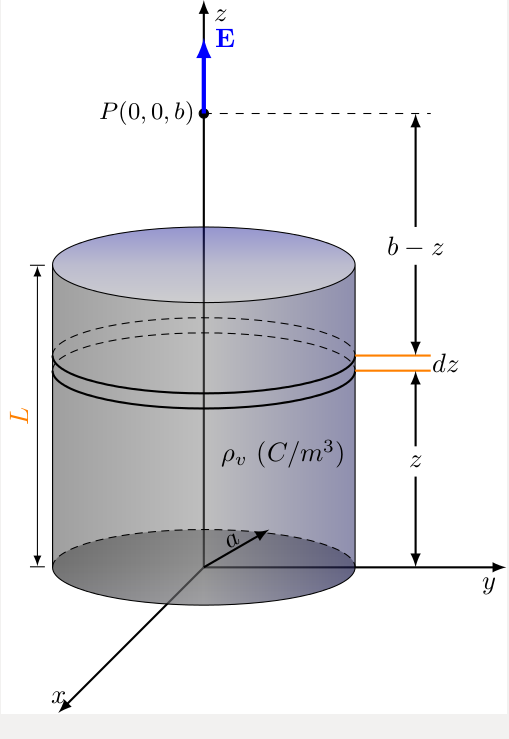
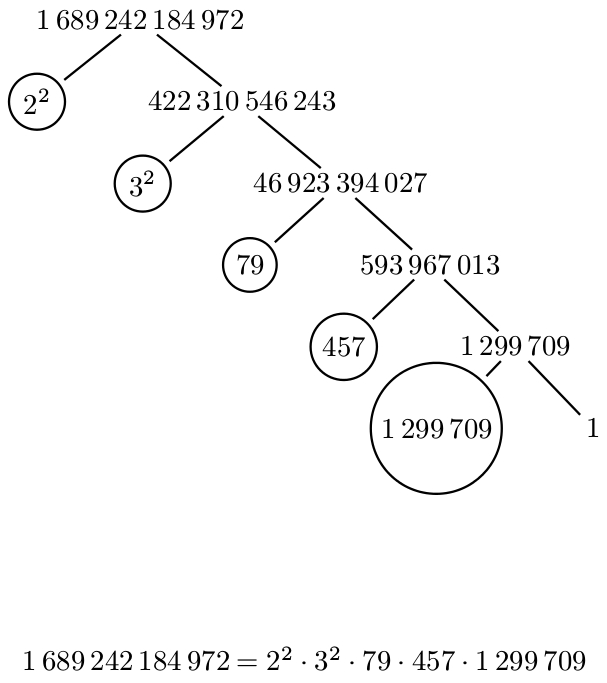
Power plant

Fossil-fuel power station (original code: http://pstricks.blogspot.com/2012/01/centrale-thermique-flammes-schematisee_07.html)

\documentclass[
  landscape
]{article}

\usepackage[utf8]{inputenc}
\usepackage[
  hmargin=2cm,
  vmargin=2.5cm
]{geometry}
\usepackage{
  pst-grad,
  pst-coil,
  pstricks-add
}

\psset{
  unit=1.5
}

%-------------------------------------------------------------------------------
%--------------------- Flammefarve: Kontinuerlig gradient ----------------------
%-------------------------------------------------------------------------------
\makeatletter
\pst@addfams{pst-HSB}
\define@key[psset]{pst-HSB}{HueBegin}{%
  \def\PstParametricplotHSB@HueBegin{#1}
}
\define@key[psset]{pst-HSB}{HueEnd}{%
  \def\PstParametricplotHSB@HueEnd{#1}
}
\define@boolkey[psset]{pst-HSB}[Pst@]{HSB}[true]{}
\psset[pst-HSB]{
  HueBegin=0,
  HueEnd=1,
  HSB=true
}
\psset{dimen=outer}

\def\parametricplotHSB{\pst@object{parametricplotHSB}}
\def\parametricplotHSB@i#1#2#3{{%
  \begin@ClosedObj
  \addto@pscode{%
    /t #1 def
    /dt #2 t sub \psk@plotpoints\space div def
    /t t dt sub def
    /Counter 0 def
    1 setlinejoin
    \psk@plotpoints {
      /t t dt add def
      /Counter Counter 1 add def
      #3
      \pst@number\psyunit mul exch
      \pst@number\psxunit mul exch
      1 Counter eq { moveto currentpoint /OldY ED /OldX ED }
        {\ifPst@HSB
          /PointY exch def
          /PointX exch def
          Counter \psk@plotpoints\space div
          \PstParametricplotHSB@HueEnd\space
          \PstParametricplotHSB@HueBegin\space sub mul
          \PstParametricplotHSB@HueBegin\space add
          1 1 sethsbcolor
          OldX OldY PointX PointY lineto lineto
          stroke
          PointX PointY moveto
      /OldX PointX def /OldY PointY def
        \else lineto \fi } ifelse
     } repeat }
   \end@ClosedObj}
  \ignorespaces}
\makeatother

\pagestyle{empty}

%-------------------------------------------------------------------------------

\begin{document}

\begin{center}
\newhsbcolor{ColorC}{.5 0.8 0}
\newhsbcolor{ColorD}{.5 0.5 0.5}
\begin{pspicture}(-3.9,-6.1)(11.8,3.5)
 {\psset{
    linewidth=3pt,
    linecolor=gray!40,
    linearc=0,
    bordercolor=black,
    border=1.1pt
  }
  \pspolygon[
    fillstyle=gradient,
    gradangle=10,
    gradbegin=orange!80,
    gradmidpoint=0,
    gradend=white
  ](-1.8,3.45)(-0.9,2)(-0.9,-1.6)(0.9,-1.6)(0.9,2.4)(-0.2,2.4)(-0.88,3.45)(-1.8,3.45)%          Brændkammeret med udfyldning
  \pspolygon(-1.8,3.45)(-0.9,2)(-0.9,-1.6)(0.9,-1.6)(0.9,2.4)(-0.2,2.4)(-0.88,3.45)(-1.8,3.45)% Brændkammerets omrids
  \pspolygon[
    linewidth=4pt
  ](-1.85,-2.65)(8.75,-2.65)(8.75,3.45)(-1.85,3.45)% Kraftværkets omrids
 }
  \pspolygon[
    linewidth=0.8pt,
    fillstyle=solid,
    fillcolor=black,
    opacity=1
  ](-1.35,-0.92)(-1.25,-0.85)(-1,-0.85)(-1,-0.95)(-0.85,-0.95)(-0.85,-1.15)(-1,-1.15)(-1,-1.45)(-1.25,-1.45)(-1.35,-1.38)% Brænder
%-------------------------------------------------------------------------------
%----------------------------------- Flamme ------------------------------------
%-------------------------------------------------------------------------------
 {\psset{
    linestyle=none,
    fillstyle=solid,
    fillcolor=yellow!50
  }
  \pscustom{%
    \pscurve(-0.87,-1)(-0.4,-0.75)(-0.55,-0.4)(-0.4,-0.13)
    \pscurve(-0.45,-0.33)(-0.2,-0.53)
    \psline(-0.2,-0.53)(-0.2,-0.97)
    \pscurve(-0.2,-0.97)(-0.6,-1.05)(-0.87,-1.01)
  }
  \pscustom{%
    \pscurve(-0.2,-0.53)(-0.17,-0.35)(0.1,-0.1)
    \pscurve(0.1,-0.1)(-0.01,-0.4)(0,-0.6)
    \pscurve(0,-0.6)(0.04,-0.52)(0.16,-0.46)
    \pscurve(0.16,-0.46)(0.1,-0.6)(0.17,-0.8)(0,-0.98)(-0.2,-0.97)
    \psline(-0.2,-0.97)(-0.2,-0.53)
  }
  \pscustom{%
    \pscurve(0.1,-0.7)(0.2,-0.6)(0.2,-0.36)(0.4,-0.1)
    \pscurve(0.4,-0.1)(0.31,-0.29)(0.33,-0.4)(0.39,-0.6)(0.3,-0.8)(0.1,-0.86)
    \psline(0.1,-0.86)(0.1,-0.7)
  }
 }
  \psframe[
    linecolor=black,
    linewidth=0.8pt,
    fillstyle=solid,
    fillcolor=black,
    opacity=1
  ](-1,-1.15)(-0.81,-0.95)
%-------------------------------------------------------------------------------
%--------------------------------- Kondensator ---------------------------------
%-------------------------------------------------------------------------------
  \pscustom[
    linestyle=none,
    fillstyle=gradient,
    gradangle=0,
    gradbegin=white,
    gradmidpoint=0,
    gradend=magenta!80
  ]{%
    \psarcn[liftpen=0](6.8,-0.2){2}{190}{165}
    \psline(!5.162 2 15 sin mul 0.2 sub)(5.162,0.92)(5.338,0.92)(!5.338 2 15 sin mul 0.2 sub)(!6.312 2 15 sin mul 0.2 sub)(6.312,0.92)(6.488,0.92)(!6.488 2 15 sin mul 0.2 sub)
    \psarcn[liftpen=0](4.8,-0.2){2}{15}{-10}
    \closepath%
  }
  \pscustom[
    linestyle=none,
    fillstyle=gradient,
    gradangle=0,
    gradbegin=blue!70,
    gradmidpoint=0,
    gradend=cyan!60
  ]{%
    \psarcn[liftpen=0](6.8,-0.2){2}{195}{190}
    \psarcn[liftpen=0](4.8,-0.2){2}{-10}{-15}
    \closepath%
  }
  \pscustom[
    linewidth=1.0pt
  ]{%
    \psarcn[liftpen=0](6.8,-0.2){2}{195}{165}
    \psline(!5.162 2 15 sin mul 0.2 sub)(5.162,0.92)(5.338,0.92)(!5.338 2 15 sin mul 0.2 sub)(!6.312 2 15 sin mul 0.2 sub)(6.312,0.92)(6.488,0.92)(!6.488 2 15 sin mul 0.2 sub)
    \psarcn[liftpen=0](4.8,-0.2){2}{15}{-15}
    \closepath%
  }
%-------------------------------------------------------------------------------
%------------------------- Vandledning i brændkammeret -------------------------
%-------------------------------------------------------------------------------
 \psset{
   coilheight=0.495,
   coilwidth=1.3,
   coilaspect=52
 }
  \rput{90}(0,0){%
    \psCoil[
      linewidth=0.07cm,
      linecolor=black,
      doubleline=true
    ]{250}{720}
  }
  \rput(0.15,0.395){%
    \parametricplotHSB[
      linewidth=1.4mm,
      plotpoints=500,
      HueBegin=0.6,
      HueEnd=0.84
    ]{270}{90}{0.88 t cos mul 0.36 t sin mul}
  }
 {\psset{
    linewidth=0.07cm,
    linecolor=black,
    doubleline=true
  }
  \rput{90}(0,0){\psCoil{600}{1200}}
  \rput{90}(0,0){\psCoil{850}{1400}}
  \rput{90}(0,0){\psCoil{1260}{1550}}
 }
 {\psset{
    linewidth=0.045cm,
    linecolor=magenta,
    doubleline=true
  }
  \rput{90}(0,0){\psCoil{470}{1200}}
  \rput{90}(0,0){\psCoil{850}{1400}}
  \rput{90}(0,0){\psCoil{1220}{1550}}
 }
%-------------------------------------------------------------------------------
 {\psset{
    linewidth=1.47mm,
    linecolor=magenta,
    linearc=0.15,
    bordercolor=black,
    border=1.1pt
  }
  \psline(0.2,1.943)(4.1,1.943)(4.1,1.6)
  \psline(4.65,1.6)(4.65,1.943)(5.75,1.943)(5.75,1.6)
 }
 {\psset{
    arrows=->,
    arrowinset=0,
    arrowscale=1.2,
    arrowlength=0.8,
    linewidth=0.6pt
  }
  \psline(5.25,0.5)(5.25,0.1)
  \psline(6.4,0.5)(6.4,0.1)
 }
  \pscircle[
    linewidth=0.8pt,
    fillstyle=solid,
    fillcolor=blue!20!green!70
  ](8.3,-0.4){0.17}
 {\psset{
    linewidth=1.3mm,
    linecolor=blue!20!green!70,
    linearc=0.15,
    bordercolor=black,
    border=1.1pt
  }
  \psline(8.18,-0.4)(5.1,-0.4)(5.1,-0.1)(9.4,-0.1)(9.4,-1.2)
  \psline(8.423,-0.4)(9.1,-0.4)(9.1,-1.2)
 }
%-------------------------------------------------------------------------------
%------------------------------------ Flod -------------------------------------
%-------------------------------------------------------------------------------
  \multido{\rA=1.05+0.1}{6}{%
    \psplot[
      linecolor=blue
    ]{8.9}{9.8}{x 1600 mul sin 0.02 mul \rA\space sub}
  }
%-------------------------------------------------------------------------------
%----------------------------------- Turbine -----------------------------------
%-------------------------------------------------------------------------------
  \psframe[
    linecolor=black,
    fillstyle=gradient,
    gradangle=0,
    gradbegin=blue!20!green!70,
    gradmidpoint=0,
    gradend=green!10
  ](3.9,0.9)(6.6,1.6)
  \psline(4.9,0.9)(4.9,1.6)
%-------------------------------------------------------------------------------
%----------------------------- Akse og turbinehjul -----------------------------
%-------------------------------------------------------------------------------
 {\psset{
    linecolor=black,
    linestyle=none,
    fillstyle=gradient,
    gradientHSB=true,
    gradangle=0,
    gradbegin=ColorC,
    gradmidpoint=0.5,
    gradend=ColorD
  }
  \psframe[
    gradmidpoint=0.4
  ](3.7,1.2)(8.47,1.3)
  \pspolygon(4,1.35)(4.8,1.5)(4.8,1.0)(4,1.15)
  \pspolygon(5.0,1.5)(5.7,1.35)(5.70,1.15)(5.0,1.0)
  \pspolygon(5.8,1.35)(6.5,1.5)(6.5,1.0)(5.8,1.15)
 }
 {\psset{
    fillstyle=vlines,
    hatchangle=0,
    hatchsep=2pt
  }
  \pspolygon(4,1.35)(4.8,1.5)(4.8,1.0)(4,1.15)
  \pspolygon(5.0,1.5)(5.7,1.35)(5.7,1.15)(5.0,1.0)
  \pspolygon(5.8,1.35)(6.5,1.5)(6.5,1.0)(5.8,1.15)
 }
 {\psset{
    linecolor=black,
    fillstyle=solid,
    fillcolor=blue!20!green!70,
    opacity=0.6,
    dimen=inner
  }
  \psframe(3.8,1.05)(3.9,1.45)
  \psframe(6.6,1.1)(6.7,1.4)
 }
%-------------------------------------------------------------------------------
%-------------------- Generator og magnetiseringsmekanisme ---------------------
%-------------------------------------------------------------------------------
 {\psset{
    linecolor=black,
    fillstyle=gradient,
    gradangle=0,
    gradbegin=blue!60!green!70,
    gradmidpoint=0,
    gradend=green!10
  }
  \psframe[
    dimen=inner
  ](6.95,1.1)(7,1.4)
  \psframe(7,0.9)(8,1.6)
  \psframe[
    gradbegin=yellow!90,
    gradend=yellow!20,
    dimen=inner
  ](8,1.05)(8.4,1.45)
 }
 {\psset{
    linecolor=black,
    linewidth=0.8pt
  }
  \psline(7.7,0.9)(7.7,0.8)(8.3,0.8)
  \psline(7.6,0.9)(7.6,0.7)(8.3,0.7)
  \psline(7.5,0.9)(7.5,0.6)(8.3,0.6)
 }
  \multido{\rB=0.6+0.1}{3}{%
    \rput(8.38,\rB){%
      \psplot[
        linecolor=black,
        linewidth=0.6pt
       ]{-0.01}{0.16}{x 2500 mul sin 0.02 mul}
    }
  }
%-------------------------------------------------------------------------------
  \pspolygon[
    fillstyle=solid,
    fillcolor=black
  ](8.2,-0.4)(8.36,-0.31)(8.36,-0.49)
  \psframe[
    fillstyle=vlines,
    hatchangle=90,
    hatchsep=1.5pt,
    hatchcolor=red,
    linewidth=0.8pt
  ](2.2,-0.8)(2.8,-0.2)
  \pscircle[
    linewidth=0.8pt,
    fillstyle=solid,
    fillcolor=blue!70
  ](3.2,-1.1){0.25}
  \pspolygon[
    fillstyle=solid,
    fillcolor=black
  ](3.05,-1.1)(3.3,-0.96)(3.3,-1.24)
 {\psset{
    linewidth=1.47mm,
    linecolor=blue!70,
    linearc=0.15,
    bordercolor=black,
    border=1.1pt
  }
  \psline(0.2,0.035)(2.5,0.035)(2.5,-1.1)(2.99,-1.1)
  \psline(3.4,-1.1)(5.8,-1.1)(!5.8 -2 15 sin mul 0.2 sub 0.0175 add)
 }
 \psset{
   arrows=->,
   arrowinset=0,
   arrowscale=1.2,
   arrowlength=0.8,
   linewidth=0.6pt
 }
  \psline(1.6,0.035)(1.2,0.035)
  \psline(0.2,0.82)(-0.2,0.85)
  \psline(1.2,1.943)(1.6,1.943)
  \psline(5.025,1.943)(5.425,1.943)
  \psline(7.5,-0.4)(7.1,-0.4)
  \psline(7.5,-0.1)(7.9,-0.1)
%-------------------------------------------------------------------------------
 {\scriptsize
 {\psset{
    linewidth=0.6pt
  }
  \rput(-0.85,2.7){\shortstack[l]{%
    \ Gas-\strut\\[-1.25ex]\quad
    kanal\strut}
  }
  \rput(-1.2,-2){Brænder}
  \psline(-1.2,-1.9)(-1.2,-1.2)
  \rput(0.25,-2){Brændkammer}
  \psline(0.25,-1.9)(0.25,-1.2)
  \rput(3.2,-1.5){Pumpe}
  \rput(3.5,-0.4){\shortstack[c]{%
    Forvarm-\strut\\[-1.25ex]
    ningsanlæg}
  }
  \psline(2.7,1.95)(2.7,2.55)
  \rput(2.7,2.7){Damp}
  \psline(1.77,0.035)(1.77,0.22)
  \rput(1.8,0.5){\shortstack{%
    Oversprøjt-\strut\\[-1.25ex]
    ningsvand\strut}
  }
  \rput(4.4,2.8){\shortstack[c]{%
    Overtryks-\strut\\[-1.25ex]
    turbine\strut}
  }
  \psline(4.4,1.5)(4.4,2.5)
  \rput(6.1,2.8){\shortstack{%
    Undertryks-\strut\\[-1.25ex]
    turbine\strut}
  }
  \psline(6.1,1.5)(6.1,2.5)
  \rput(7.5,3.2){Generator}
  \psline(7.5,1.5)(7.5,3.0)
  \rput(8.15,2.5){\shortstack{%
    Magneti-\strut\\[-1.25ex]
    serings-\strut\\[-1.25ex]
    maskine\strut}
  }
  \psline(8.15,1.4)(8.15,2.1)
  \rput(4.2,0.1){\shortstack{%
    Konden-\strut\\[-1.25ex]
    sator\strut}
  }
  \psline(4.5,0.1)(5.1,0.1)
  \rput(7.7,-0.8){Kølevand}
  \psline(7.7,-0.4)(7.7,-0.6)
  \rput(9.3,-1.8){Flod}
 }
 }
%-------------------------------------------------------------------------------
 \rput(-2,-4.5){%
  \psset{
    arrows=->,
    ArrowFill=true,
    arrowinset=0,
    arrowscale=0.7,
    arrowlength=0.5,
    framearc=0.05,
    linecolor=gray!40,
    dimen=outer
  }
  \psline[
    linewidth=0.7cm
  ](12,0)(14,0)
  \psline[
    linewidth=0.2cm,
    linearc=0.3
  ](12,-0.35)(12.5,-0.35)(12.5,-1.0)
  \psframe[
    linecolor=black
  ](10,-0.8)(12,0.8)
  \psline[
    linewidth=0.9cm
  ](8,0)(10,0)
  \psline[
    linewidth=0.2cm,
    linearc=0.3
  ](8,-0.45)(8.5,-0.45)(8.5,-1.1)
  \psframe[
    linecolor=black
  ](6,-0.8)(8,0.8)
  \psline[
    linewidth=1.1cm
  ](4,0)(6,0)
  \psline[
    linewidth=0.2cm,
    linearc=0.3
  ](4,-0.55)(4.5,-0.55)(4.5,-1.2)
  \psframe[
    linecolor=black
  ](2,-0.8)(4,0.8)
  \psline[
    linewidth=1.3cm
  ](0,0)(2,0)
  \psline[
    linewidth=0.2cm,
    linearc=0.3
  ](0,-0.65)(0.5,-0.65)(0.5,-1.3)
  \psframe[
    linecolor=black
  ](-2,-0.8)(0,0.8)
  \rput(-1,0){Brænder}
  \rput(3,0){Kedelrør}
  \rput(7,0){Turbine}
  \rput(11,0){Generator}
  \textcolor{red}{%
    \rput(0.55,0){\shortstack[l]{%
      \footnotesize Termisk\strut\\[-1.25ex]
      \footnotesize energi\strut}
    }
    \rput(4.6,0){\shortstack[l]{%
      \footnotesize Potentiel\strut\\[-1.25ex]
      \footnotesize energi\strut}
    }
    \rput(8.55,0){\shortstack[l]{%
      \footnotesize Kinetisk\strut\\[-1.25ex]
      \footnotesize energi\strut}
    }
    \rput(12.6,0){\shortstack[l]{%
      \footnotesize Elektrisk\strut\\[-1.25ex]
      \footnotesize energi\strut}
    }
    \rput(0.5,-1.5){\footnotesize Spildt energi}
    \rput(4.5,-1.4){\footnotesize Spildt energi}
    \rput(8.5,-1.3){\footnotesize Spildt energi}
    \rput(12.5,-1.2){\footnotesize Spildt energi}
  }
}
\end{pspicture}
\end{center}

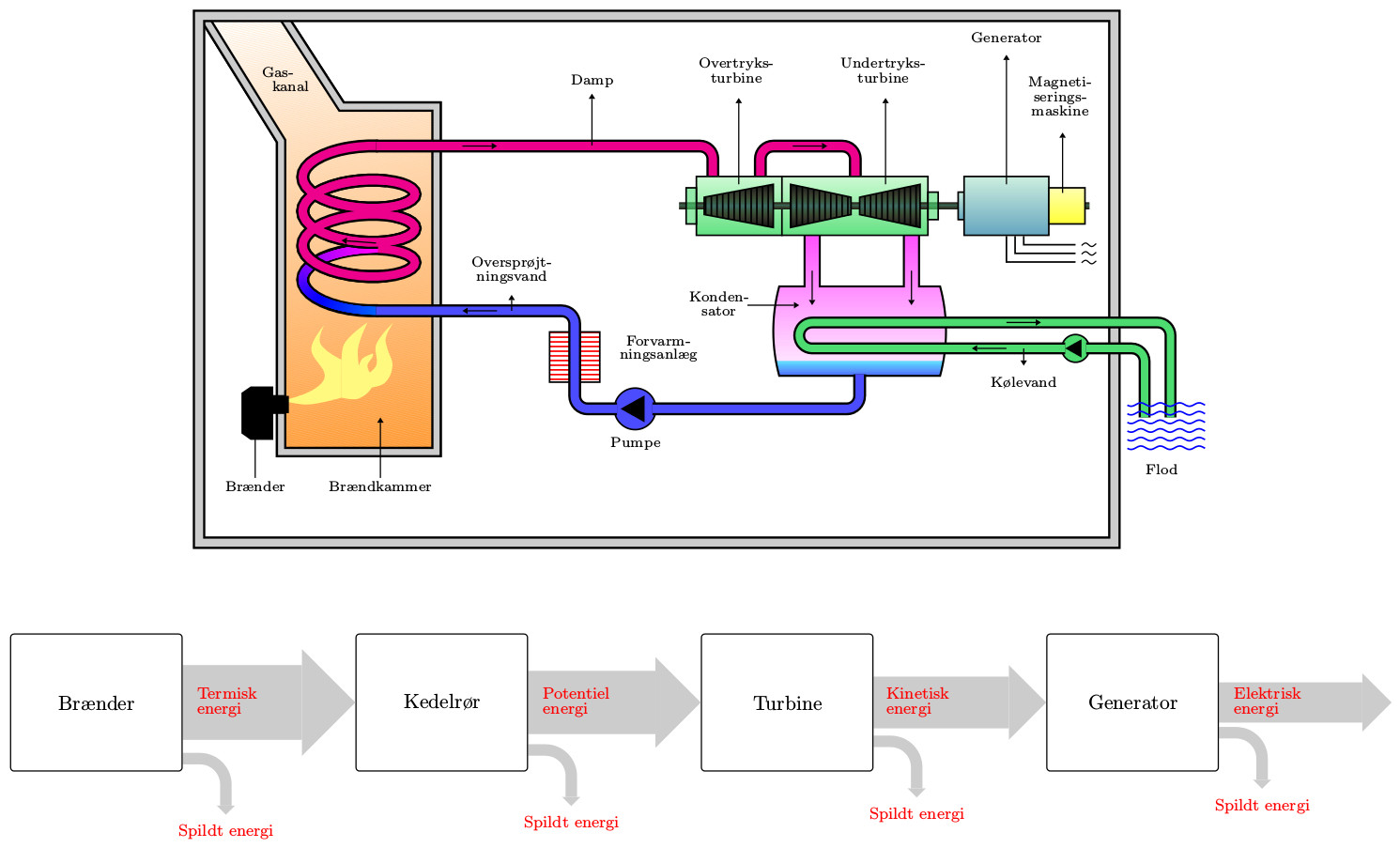
Note that the text is converted into Danish.

Note: At pstricks.blogspot.com/2013/06/un-schema-de-centrale-electrique.html one can see a drawing of a nuclear power plant. I would've liked to add this code too, but I'm limited to 30k characters.

Answer 28

Edit: Oops, realized too late this was about images drawn using latex.

Typing up a conference paper for ICGG 2014 in Innsbruck about phase spaces and fitness landscapes. Although I'm a programmer for a 3D CAD company, I've grown very tired of rendered images as of late. I find it very difficult to draw focus to specific salient details in a digital image.

Although I heavily rely on 3D software and custom programming to generate the geometry in these images, everything is ultimately hand-drawn. Labels are added directly in LaTeX using \put commands, so the images are kept clean.

Not sure what anyone is going to learn from the code, but here is the tex for the bottommost image:

\begin{figure}[H] \centering
\begin{overpic}[width=.95\linewidth]{Images/OverconstrainedLandscape}
 \put (40,15) {\smaller[2] $\nicecirc{1}$}
 \put (66,35) {\smaller[2] $\nicecirc{1}$}
 \put (3,46)  {\smaller[2] $\nicecirc{2}$}
 \put (45,55) {$\pazocal{L}^\prime$}
\end{overpic}
\caption{Geometry of overconstrainedness}
\label{fig:overconstrainedlandscape}
\end{figure}

Answer 29

A cylindrical volume charge distribution and its electric field strength on the point (0,0,b).

\documentclass{standalone}
\usepackage{tikz} 
\usetikzlibrary{calc}    
\tikzset{
  dim above/.style={to path={\pgfextra{
        \pgfinterruptpath
        \draw[>=latex,|<->|] let
        \p1=($(\tikztostart)!2mm!90:(\tikztotarget)$),
        \p2=($(\tikztotarget)!2mm!-90:(\tikztostart)$)
        in(\p1) -- (\p2) node[pos=.5,sloped,above]{#1};
        \endpgfinterruptpath
      }(\tikztostart) -- (\tikztotarget) \tikztonodes
    }
  },
  dim below/.style={to path={\pgfextra{
        \pgfinterruptpath
        \draw[>=latex,|<->|] let 
        \p1=($(\tikztostart)!2mm!90:(\tikztotarget)$),
        \p2=($(\tikztotarget)!2mm!-90:(\tikztostart)$)
        in (\p1) -- (\p2) node[pos=.5,sloped,below]{#1};
        \endpgfinterruptpath
      }(\tikztostart) -- (\tikztotarget) \tikztonodes
    }
  },
}

\begin{document}
  \begin{tikzpicture}

\draw[thick,-latex] (0,0,0) -- (4,0,0) node[anchor=north east]{$y$};
\draw[thick,-latex] (0,0,0) -- (0,7.5,0) node[anchor=north west]{$z$};
\draw[thick,-latex] (0,0,0) -- (0,0,5) node[anchor=south]{$x$};
\filldraw (0,6,0) circle (1.75pt) node[left,font=\small]{$P(0,0,b)$};

\fill[top color=gray!50!black,bottom color=blue!10,middle color=gray,shading=axis,opacity=0.25] (0,0) circle (2cm and 0.5cm);
\fill[left color=gray!50!black,right color=blue!50!black,middle color=gray!50,shading=axis,opacity=0.25] (2,0) -- (2,4) arc (360:180:2cm and 0.5cm) -- (-2,0) arc (180:360:2cm and 0.5cm);
\fill[top color=blue!90!,bottom color=blue!2,middle color=blue!30,shading=axis,opacity=0.25] (0,4) circle (2cm and 0.5cm);
\draw (-2,4) -- (-2,0) arc (180:360:2cm and 0.5cm) -- (2,4) ++ (-2,0) circle (2cm and 0.5cm);
\draw[densely dashed] (-2,0) arc (180:0:2cm and 0.5cm);

\draw[densely dashed] (-2,2.8) arc (180:0:2cm and 0.5cm);
\draw[densely dashed] (-2,2.6) arc (180:0:2cm and 0.5cm);
\draw[thick] (-2,2.8) arc (180:360:2cm and 0.5cm);
\draw[thick] (-2,2.6) arc (180:360:2cm and 0.5cm);
\draw[thick, orange] (2,2.6) -- (3,2.6);
\draw[thick, orange] (2,2.8) -- (3,2.8);
\draw[thick,-latex] (2.8,4) -- (2.8,2.8);
\draw[thick,-latex] (2.8,1.6) -- (2.8,2.6);
\draw[thick,latex-] (2.8,0) -- (2.8,1.2) node[above] {$z$};
\draw [dashed] (0,6)--(3,6);
\draw[thick,latex-] (2.8,6) -- (2.8,4.5)node[below]{$b-z$};
\node at (3.5,2.7) [anchor=east]{$dz$};
\node at (2,1.5) [anchor=east]{$\rho_v\ (C/m^3)$};
\draw (-2,0) to[dim above=$L$,color=orange] (-2,4) ;

\coordinate (vec1) at (30:1);
\draw[-latex,thick] (0,0) -- (vec1)node[midway,sloped, above, inner sep=1] {$a$};
\draw[ultra thick,-latex,blue] (0,6,0) -- (0,7,0) node[right] {$\mathbf{E}$};
     \end{tikzpicture}  
\end{document}

Answer 30

Prime factorization

\documentclass{article}

\usepackage{pst-tree}
\usepackage{xintexpr}
\usepackage{siunitx}

\psset{
  levelsep=1,
  treesep=1,
  nodesep=2pt
}

\catcode`\_ 11

% This code (non-expandable) produces {{}{}{N}} followed by
% successive braced triplets {{p}{k}{m}} where p is
% a prime factor of N,  k its exponent in N, and m is
% the result of dividing N by p^k and all previous
% powers of smaller primes. So, the last triplet has m = 1.

% The code uses package xint to be able to deal
% with numbers larger than the TeX limit of 2^{31}-1
% on count registers. 

\def\factorize#1{%
    \edef\factorize_N{#1}%
    \def\factorize_exp{0}%
    \edef\factors{{{}{}{\factorize_N}}}%
    \factorize_i
}

\def\factorize_i{%
    \xintiiifOdd{\factorize_N}%
      {\factorize_ii}%
      {\edef\factorize_exp{\xintInc{\factorize_exp}}%
       \edef\factorize_N  {\xintHalf{\factorize_N}}%
       \factorize_i}%
}

\def\factorize_ii{%
    \xintiiifZero{\factorize_exp}%
      {}%
      {\edef\factors{\factors{{2}{\factorize_exp}{\factorize_N}}}}%
    \xintiiifOne{\factorize_N}%
      {}%
      {\def\factorize_M{3}%
       \def\factorize_exp{0}%
       \factorize_iii}%
}

\def\factorize_iii{%
    \xintAssign\xintiiDivision\factorize_N\factorize_M\to\factorize_Q\factorize_R
    \xintiiifSgn{\factorize_R}%
      {% never happens: remainder can not be negative
      }%
      {% case of vanishing remainder
       \edef\factorize_exp{\xintInc{\factorize_exp}}%
       \let\factorize_N\factorize_Q 
       \factorize_iii
      }%
      {\factorize_iv}% 
}

\def\factorize_iv{%
    \xintiiifZero{\factorize_exp}%
      {}%
      {\edef\factors{\factors{{\factorize_M}{\factorize_exp}{\factorize_N}}}}%
    \xintiiifOne{\factorize_N}%
      {}%
      {% here N>1, N=QM+R (0<R<Q) is < M(Q+1) and N has no prime factors
       % at most equal to M. If a prime P>M divides N, the
       % quotient N/P will be < Q+1, hence at most Q. If Q<=M, then
       % N/P must be 1 else there would be some prime <=M dividing N.
       % no \xintiiifGeq ...
       % \xintiifCmp will have branches for each of <, =, >, less convenient
       % So we use \xintiiifLt which exists, and permute the branches
       % compared to original code
       \xintiiifLt\factorize_M\factorize_Q
         {% we go on testing with bigger factors
          % or \edef\factorize_M{\xintInc{\xintInc{\factorize_M}}} perhaps
          \edef\factorize_M{\xintiiAdd \factorize_M 2}%
          \def\factorize_exp{0}%
          \factorize_iii
         }%
         {% implies that N is prime
          \edef\factors{\factors{{\factorize_N}{1}{1}}}% we stop here
         }%
      }%
}

\catcode`\_ 8

% We now define the macro \FactorTree which will produce
% a tree displaying the factorization.

\newtoks\FactorTreeA
\newtoks\FactorTreeB

\makeatletter

\newcommand*\FactorsToTree[1]{%
    \FactorsToTree@ #1%
}

% Macro which was used to produce the images;
% variant follows which skips the exponents equal to 1.

% \newcommand*\FactorsToTree@[3]{%
%     \xintSgnFork{\xintCmp{#3}{1}}% check to see if end has been reached
%     {}%
%     {\FactorTreeA\expandafter{\the\FactorTreeA
%                               \Tcircle{$\num{#1}^{#2}$}%
%                               \TR{1}%
%                               }}%
%     {\FactorTreeA\expandafter{\the\FactorTreeA 
%                              \Tcircle{$\num{#1}^{#2}$}%
%                              \psTree{\TR{\num{#3}}}}%
%      \FactorTreeB\expandafter{\the\FactorTreeB \endpsTree}}%
% }


% This variant will not print the exponents equal to 1:

\newcommand*\FactorsToTree@[3]{%
    \ifnum 0#2=1 % First triplet has an empty #2, hence the trick with 0.
       \expandafter\@firstoftwo
    \else
       \expandafter\@secondoftwo
    \fi
    % Exponent #2 is 1, so don't print it.
    {\xintSgnFork{\xintCmp{#3}{1}}% Check to see if end has been reached.
    {}%
    {\FactorTreeA\expandafter{\the\FactorTreeA
                              \Tcircle{$\num{#1}$}%
                              \TR{1}%
                              }}%
    {\FactorTreeA\expandafter{\the\FactorTreeA 
                             \Tcircle{$\num{#1}$}%
                             \psTree{\TR{\num{#3}}}}%
     \FactorTreeB\expandafter{\the\FactorTreeB \endpsTree}}}
    % Exponent #2 is > 1 (or absent in the {}{}{N} triplet).
    {\xintSgnFork{\xintCmp{#3}{1}}% Check to see if end has been reached.
    {}%
    {\FactorTreeA\expandafter{\the\FactorTreeA
                              \Tcircle{$\num{#1}^{#2}$}%
                              \TR{1}%
                              }}%
    {\FactorTreeA\expandafter{\the\FactorTreeA 
                             \Tcircle{$\num{#1}^{#2}$}%
                             \psTree{\TR{\num{#3}}}}%
     \FactorTreeB\expandafter{\the\FactorTreeB \endpsTree}}}%
}

\makeatletter
\def\@factorinliner #1{\@factorinliner@#1}
\def\@factorinliner@#1#2#3{%
  \ifnum #2>1 \expandafter\@firstoftwo\else
              \expandafter\@secondoftwo\fi%
  {{#1}^{#2}}{\num{#1}}%
}
\newcommand*\FactorizeInline[1]{%
  \factorize{#1}% 
  \xintListWithSep\cdot
    {\xintApply\@factorinliner{\expandafter\@gobble\factors}}%
}%

\newcommand*\FactorTree[1]{%
    \factorize{#1}%
    \FactorTreeA{\@gobbletwo}%
    \FactorTreeB{}%
    \xintApplyUnbraced\FactorsToTree{\factors}%
    \the\FactorTreeA\the\FactorTreeB
    \vspace{12ex}
    $\num{#1} = \FactorizeInline{#1}$
}

\makeatother


\begin{document}

\FactorTree{1689242184972}

\end{document}