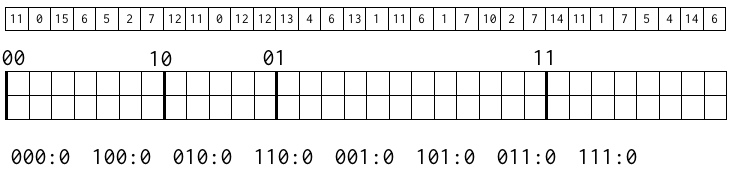ウェーブレット行列の構築方法について。
前に書いた記事とは違って、「ウェーブレット行列大好き!」って人*1以外が読んでもあんまり益がない記事だということをあらかじめ書いておく。
内容としては、相変わらず中学生以上の知識が必要ということはないけれど。
上の記事で書いたように、ウェーブレット行列は 2進数の基数ソートと同じような感じで構築できる。
で、基数ソートをするには、元の配列と同じだけの領域が必要になる。
だが、ウェーブレット行列のように各段階でのビット列だけが必要であるなら、その領域は必要ない。
ウェーブレット行列でも、ウェーブレット木のノードのようなものを持っておくことで、配列長のオーダーでなく、文字の種類のオーダー(一般的に配列長よりずっと小さい)だけの記憶領域で構築できる。
ぼくのウェーブレット行列ライブラリである wavelet-matrix-cpp や、 id:echizen_tm さんの Shellinford では、それぞれ独立に、少し違ったやり方でそれを実装している。
これらのやり方はけっこうめんどくさいことになる。
ぼくも最近 Shellinford のソースを読んだけど、似たようなことやってるはずなのに頭がフットーしそうになってしまった。
で、ぼくのやり方にも、やっぱり少しは人間にやさしい解説記事を書いておかないといけないかなーと思って、書いてみることにした。
感覚的な記事なので、あんまり厳密なものにはならないと思う。
まず、ウェーブレット行列の作り方は基数ソートと同じで、ただ順番が下のビットから上のビットではなく、上のビットから下のビットに向けて実行するというところが違う。
また、基数ソートをするといっても、最終的なソート結果は使わないで、記録するのはソートの途中経過で見たそれぞれのビット列だけ。
このビット列は、実際にソートをしないでも作れる。
なぜか。
まず、n 段階目でするべきことは、基数ソートによって上から n-1 ビット目までソートされた数字列の n ビット目を記録すること。
で、上から n-1 ビット目までソートされているということは、上から n-1 ビット目までの数字はひとかたまりになっている。
その、上から n-1 ビット目まででソートされた数字の、それぞれの「ブロック」の開始位置がわかればいい。
それがわかれば、最初の数字列はそのままで、上から n-1 ビット目までを見て、それに対応するブロックに左から書き込んでいくだけ。
さらに、そのことによって、「上から n ビット目までソートされた数字ブロックのそれぞれの開始位置」がわかると、帰納的にうまくいく。
自分で書いていても何を書いているかわからないので、実例で説明する。
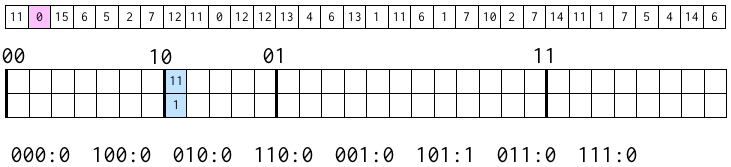
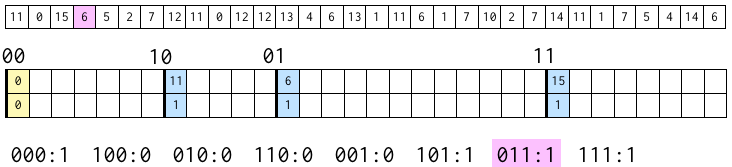
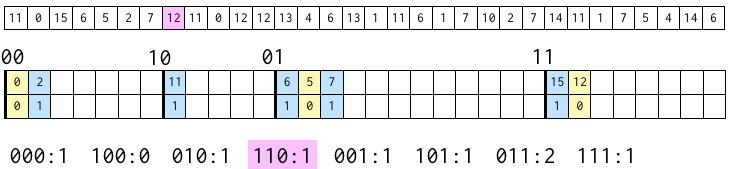
ここでの例は、0〜15 までの 4 ビットの数字からなる長さ 32 の配列で、上から 1 ビット目・2 ビット目のビット列を作り終わって、上から 3 ビット目のビット列を作るところ。
次の図で、上の配列は元の配列(ソートされていない)。
真ん中の空の表は、上の 2 ビットが 00, 10, 01, 11 のブロックが、今の段階でそれぞれどこから始まるかというもの。
下の数字は、次の段階で上の 3 ビットが 000, 100, 010, 110, 001, 101, 011, 111 のブロックがそれぞれいくつの数字を含むかを覚えておくもの。
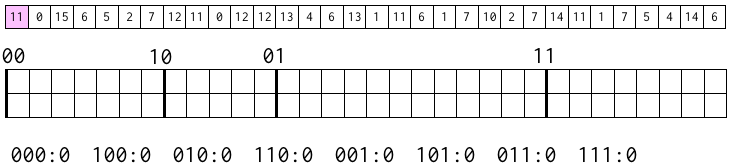
まず、最初の数字 11 に注目。
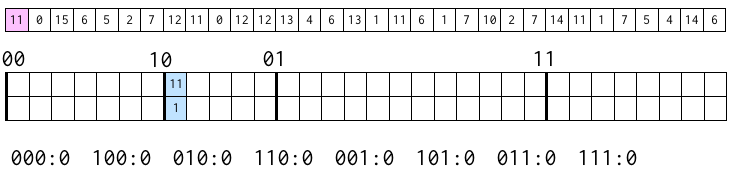
この数字は、2進数で表すと 1011。つまり、上から 2 ビットは 10 となる。そのため、10 のブロックの最初の位置に置く。
表の上には元の数字、下にはその 3 ビット目(この場合は 1)を書いてある。
このとき、実際に書き込むのは下のほうだけだが、説明のために表の中では上に元の数字を書くことにする。
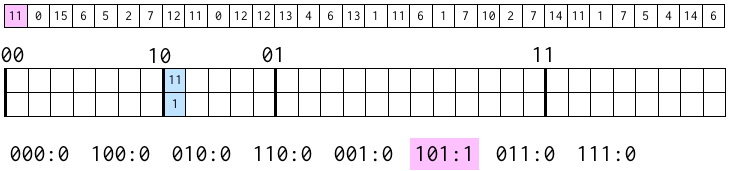
そして、上から 3 ビットが 101 であるブロックに含まれる数字の数に 1 を足す。
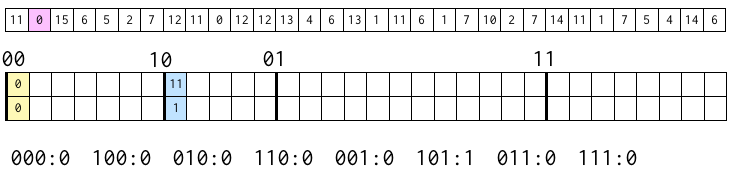
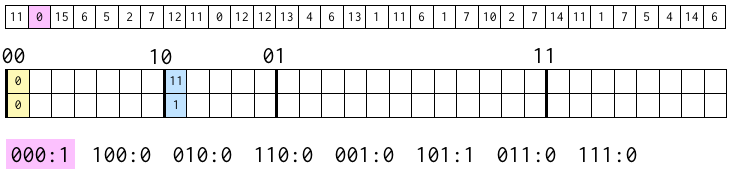
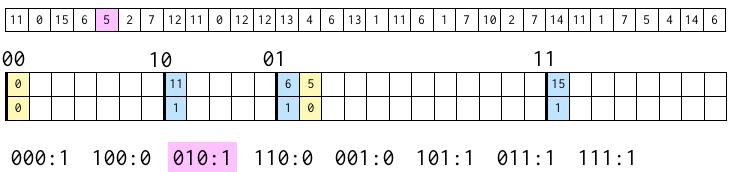
今度は、次の数字 0 に注目。
上から 2 ビットは 00 になるので、00 のブロックの最初の位置に、3 ビット目である 0 を書き込む。
そして、上から 3 ビットが 000 であるブロックに含まれる数字の数に 1 を足す。
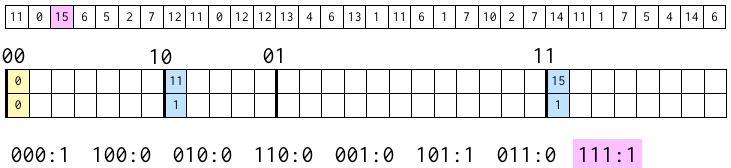
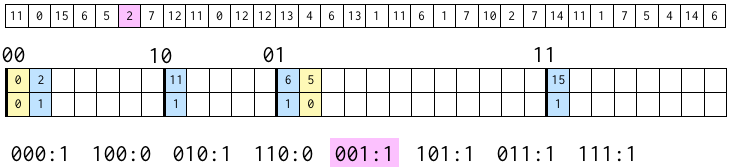
次は 15。
上から 2 ビットが 11 であるブロックに、3 ビット目である 1 を書き込み、上から 3 ビットが 111 であるブロックに含まれる数字の数に 1 を足す。
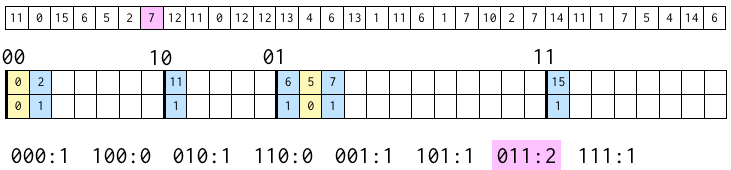
次は 6。
上から 2 ビットは 01、3 ビット目は 1、上から 3 ビットが 011 であるブロックに含まれる数字の数に 1 を足す。
次は 5。
上から 2 ビットは 01、3 ビット目は 0。010 のブロックの数字の数をインクリメント。
2。
7。
12。
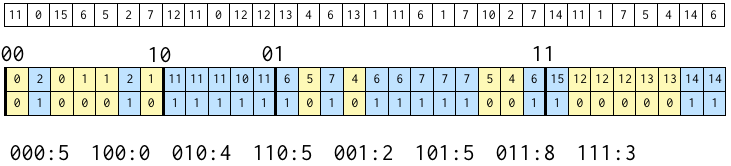
これを最後まで続けると、次のようになる。
で、000, 100, 010, ..., 111 のそれぞれのブロックに含まれる数字の数がわかることになる。
図にすると、次のようになる。
これらの数字を先頭から足し合わせて、右にひとつずらすと、それぞれのブロックの開始位置になる。
こういうわけで、上から 3 ビット 000, 100, 010, ..., 111 である数字が次の段階でそれぞれどこから始まるかがわかることになった。
つまり、次の段階も同じように構築できることになる。
この中で、「上から 2 ビットが ×× である数字のブロックの開始位置」というのは、00, 10, 01, 11 のように、ビットを逆にしたものの順に並んでいる。
次のレベルでは、000, 100, 010, 110, 001, 101, 011, 111。
で、これらは配列にそのまま入れておいて、ビット逆順にループしていく。
で、ここで計算したそれぞれのブロックの開始位置は、ウェーブレット木のノードにあたるようなものになる。
そして、それはこの記事で書いたように、配列先頭からの RankLessThan() や QuantileRange() を高速化するのに使うことができる。
この構築方法には次のような利点がある。
- 配列をコピーしないでいい。
- ノードの開始位置が計算できて、後で高速化に使える。
しかし、次のような欠点が。
- 書き込み位置がバラバラになるので、キャッシュミスを引き起こす。
- ノードの開始位置を覚えておくのに、アルファベット数のオーダーの余分な領域が必要。
2 番目のほうは、一般にアルファベット数は配列長よりだいぶ小さいので、あまり問題にならない。
問題は 1 番目。
それぞれの段階で、元の配列をそのまま先頭から見ていって、上位 n ビットによって適切な位置にビットを立てていくことになるのだが、段階が進むにつれて、どんどん書き込み位置がバラバラになっていく。
そして、それがひどいキャッシュミスを引き起こす。
最近、wavelet-matrix-cpp について問い合わせがあった。
大きなデータを食わすと途中からものすごく遅くなるそうだ。
で、元配列をコピーしないで済んで、さらにキャッシュミスを引き起こさないような構築方法はないかと。
何かいい方法はないかなぁ。
*1:ぼく自身そこまででもないけど。