Statistical Error in Simple Linear Regression

Question

I want to start off this question by saying that I'm looking for more of a conceptual understanding of this term in a simple regression model, not a mathematical one.

In econometrics, simple linear regression has an "error term", called mu, which represents "factors other than x that effect y, or unobserved data." In a statistics class, this term is called "statistical error" or "noise" treated as epsilon, which again is random noise in the real world our model cannot capture.

In Introduction to Statistical Learning, this term is referred to as "irreducible error," and is a quantity that represents unmeasured variables that we haven't measured, or simply just unmeasurable variation in real world data. The authors bifurcate between this term and reducible error.

Here is where my confusion lies: in a theoretically, completely deterministic world, where we have an infinite amount of data, is this "irreducible error" theoretically reducible? That is to say, if in this theoretical world, our covariate, college GPA, could be mapped to our response, say "Salary," could this term technically be zero?

I understand that in the world we live in, there is always unmeasurable variation in data, and that we'll never have access to an infinite amount of data or know beforehand every single covariate, thus this error arises. But say we had 5 data points, and this was our "theoretical population," would this "irreducible error" term disappear?

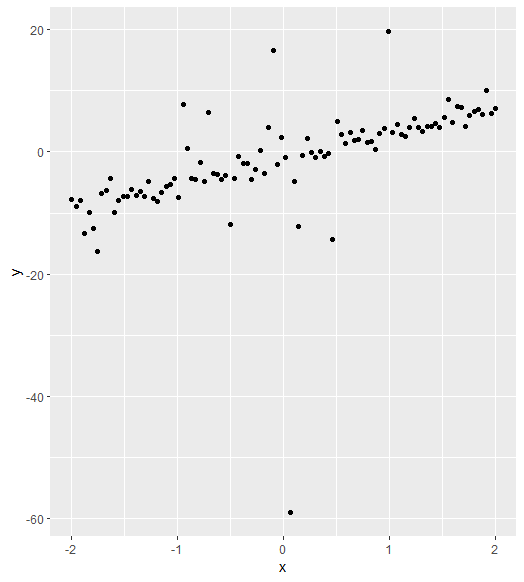
For example, in Introduction to Statistical learning, they have this image:

My confusion in this image arises from the fact that this data was simulated, and so we actually know the true underlying function f. But if that is the case, why is there still error? If we know f, why can't we perfectly fit this function to the data? And if this data was simulated based on f, why doesn't the simulation produce data points on the function f?

I know it may seem like a silly question, but I'm trying to understand the nuance here. Many thanks to your help in advance.

Answer 1

Yes, you know $f$. There’s still something more to the points than $f$. The $f$ just gives the conditional expected value, conditioned on the feature value(s). Then the point is drawn from a distribution that has such a mean but also has (potentially) positive variance. Thus, each point $y_i$ can be written as:

$$ y_i = f(x_i) + \varepsilon_i $$

That is, the observed point $y_i$ is equal to the expected value, given by $f(x_i)$, plus some deviation from t the expected value.

If you don’t know what the deviations are, such as if they are random variables, then you don’t know exactly what the point will be, even if you exactly know the expected value. If you do know what the deviation is, the $f(x_i)$ wasn’t really the expected value, was it? The expected value is whatever $f(x_i)$ is plus the known deviation from $f(x_i)$. In fact, beyond being the expected value, that is the certain value.

The latter case is deterministic. However, the simulation you cite has a random component, so you don’t know what the observed $y_i$ will be, even if you perfectly know its expected value given by $f$.

THE SIMULATION FROM MY COMMENTS

Run the following in R.

library(ggplot2)
# set.seed(not telling)
N <- 100
a <- -2
b <- 2
x <- seq(a, b, (b - a)/(N - 1))
Ey <- 4*x - 1
plot(x, Ey)
e <- rt(N, 1.1)
y <- Ey + e
d <- data.frame(
  x = x,
  y = y
)
ggplot(d, aes(x = x, y = y)) +
  geom_point()

I get this plot.

You did not get the same plot, even though you know the conditional expected value, the $f(x)$, is $4x - 1$? It's almost as if I denied you a piece of information.

Now set the seed as 2024.

library(ggplot2)
set.seed(2024)
N <- 100
a <- -2
b <- 2
x <- seq(a, b, (b - a)/(N - 1))
Ey <- 4*x - 1
plot(x, Ey)
e <- rt(N, 1.1)
y <- Ey + e
d <- data.frame(
  x = x,
  y = y
)
ggplot(d, aes(x = x, y = y)) +
  geom_point()