Chi-Squared-Test fails for large sample size?

Question

I am currently working on an exercise for my statistics class and I came across some weird behaviour of the Chi-Squared-test (CST), which I hoped someone could explain to me.

The problem is the following:

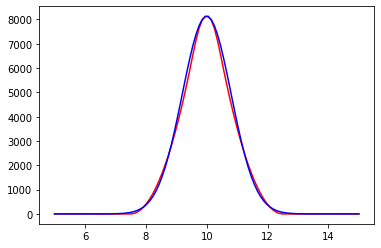
I calculated the Chi-Squared-test for a sample that is illustrated in Figure 1. I generated that sample from a normal distribution using the parameters I then tested within my CST. I therefore expect my CST to tell me that the sample comes from the specified distribution -- which CST successfully does.

[Figure 1. Red: Sample, Blue: normal distribution]

Now, I take some other data, illustrated in Figure 2. As one can see, the data is pretty close to the normal distribution on which I carry out my CST. However, my CST fails, telling me that my data DOES NOT come from the normal distribution with the specified parameters.

[Figure 2. Red: Sample, Blue: normal distribution]

I figured that with increasing sample size the CST becomes worse and worse. How is that possible when my data seems to fit so well?

---

EDIT 1

The figures illustrate the following: The blue curve shows my the distribution which I underlie my CST, i.e. i want to check whether my samples (red) are from the blue distribution. The CST test itself is not illustrated, I just used python tool (included in scipy package) for that. The samples differ vastly in size, i.e. in Figure 1 a sample size of $100$ was used, whereas Figure 2 shows a sample size of $\sim 150 \, 000$.

Answer 1

This is common to observe, and it is a feature of hypothesis testing, not a bug.

The null hypothesis is that your distribution is equal to some specified distribution. Thus, if your distribution is almost equal to the specified distribution, they are unequal, and the null hypothesis is false.

As you increase your sample size, you increase your ability to detect small differences. Eventually, you have the ability to detect tiny differences.

However, those differences are there, and the test is doing exactly what it is supposed to do.

You're right that the two plots look very similar. They are not the same, and your large sample sizes gives you the ability to detect that difference.