1
$\begingroup$

So I know this may be basic but I'm having trouble piecing together the right formulas and logic to understand this. Most of the Z-tables online seem to have different information than the one provided to us so I've left the table below. Its a centered Z-table and not a left tail one.

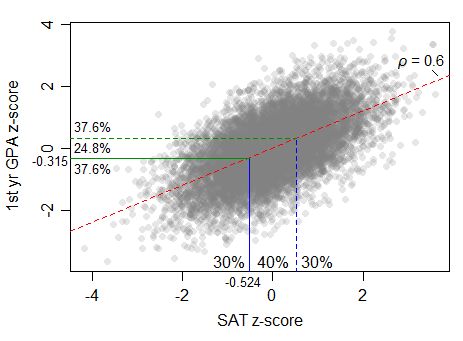
For first year students at a university the correlation between SAT scores and first year GPA is 0.60. The scatter diagram is football shaped. Predict the first year GPA for a student whose percentile rank on the SAT was 30%.

In order to get the proper z-score I subtracted the remaining percent twice from 100%. I dont follow the logic behind this but apparently it works. |100 - 70 - 70| = 40%. The z score corresponding to 40% of the area on our table is ~.53

I then multiplied by the correlation to get ~0.32 (this makes sense to me). This corresponds to about 25%. I'm not quite sure how to then get this number back into percentile. The answer is 38%.

Thanks for the help! Z-Table

Improve this question
$\endgroup$
2
  • $\begingroup$ Note on the table: The central areas have been multiplied by 100 to give percentages, okay, I can get that, but for a standard normal the "heights" are nonsense since they're not percentages of anything. They should not be multiplied by 100. $\endgroup$
    – Glen_b
    Commented Sep 28, 2017 at 3:43
  • $\begingroup$ The correct calculation for your |100-70-70| is 100-30-30 = 40 (no absolute value involved, no subtracting 30 from 100). from 100% you subtract the portion in the left tail (30%) and the same proportion in the right tail (another 30%) leaving the part in the middle (40%). The correct calculation is more direct, easier to understand and faster, but will yield the same result as your approach that doesn't have the same simple justification. $\endgroup$
    – Glen_b
    Commented Sep 28, 2017 at 3:46

1 Answer 1

Reset to default
1
$\begingroup$

You almost got there.

Your 0.32 would more accurately be 0.315 (for number of sd's below the mean). This gives a central area of about 25% and a left tail area of about 38%. More accurately, (100-24.8)/2=37.6 (Your 24.8 is 100-?-? = 24.8 and you want to figure out what that ? value would be)

Plot of bivariate distribution illustrating the steps in the question and the last step here (1-0.248)/2 = 0.376

Improve this answer
$\endgroup$

Your Answer

By clicking “Post Your Answer”, you agree to our terms of service and acknowledge you have read our privacy policy.

Not the answer you're looking for? Browse other questions tagged or ask your own question.