Assuming μ(x1,..,xm) is a function for calculating the average of those variables, you can in fact simplify your calculation greatly. Firstly, note that for each possible assignment of x_k, you are going to alternate between two probabilities, 1/2 and 1-q, or 1/2 and q. Say m=3, and z_1=z_2=z_3=1. If not for the μ(...), we could write:
ν(z_1, z_2, z_3) = (1/2 + q) * (1/2 + q) * (1/2 + q)
This factoring would allow us to save quite a bit of computation. In order to extend this approach to the case with μ, note that we can pull that factor out in front of the product, raising it to the power of m. This brings us closer, so now if we could just group the like-sums of our concise product above so we can multiply each by their correct μ(...)^m factor, we could be done.
The way we do this is by introducing an artificial variable, y. Let each power of y represent another x_i=1. That is, for z_i=1 and x_i=1, we have y/2, and for z_i=1, x_i=0 we have q as before. This makes our previous product:
(y/2 + q) ^ 3 = q^3 + 3*q^2*y/2 + 3*q*y^2/4 + y^3/8
You'll see that the coefficients of our polynomial are the partial sums of our previous product, organized by count of x_i=1 terms. This enables us to compute our average for each term, multiply by the coefficient, and sum. Put a bit more explicitly:
ν(z_1, z_2, z_3) = (0/3)^3 * (q^3) + (1/3)^3 * (3*q^2/2) + (2/3)^3 * (3*q/4) + (3/3)^3 * (1/8)
So, if you have z_1=1, z_2=0, z_3=1, do:
ν(1, 0, 1) => P(y) = (y/2 + q) * (y/2 + 1 - q) * (y/2 + q)
Then use the FFT to multiply each term (combining smallest order terms first, building up) to get the full expression. Once you have the coefficients, calculate μ(...)^m for each term based on its order, multiply, and sum as before.
All in all, this will put you at a O(n log^2(n)) time evaluation, with time dominated by the repeated FFT to get the full polynomial P(y).

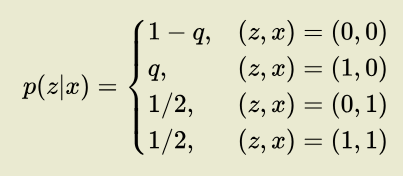
μ(x1,..,xm)the average ofx1...xm? (2) Is sum_{x1,...,xm} summing over all 2^m assignments of x1...xm, or is there an explicit subset of valid assignments?