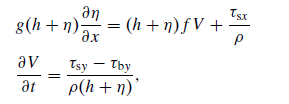Solving coupled PDE with python

Question

I do not understand how to solve for the eta and V in my coupled PDE equations using python or a python ode solver. (Or is it possible to do a numerical solution for these couple equations without a solver?) I have spent several days on this but I still cannot understand how to start! Any hints would be helpful . I understand the example given in

Solve 4 coupled differential equations in MATLAB

but I still need more hints to figure out how to apply these principles to my coupled PDEs below.

I would like to plot a timeseries of eta and V, given forcing inputs of varying timeseries of tau.

x is a point in space, and t is a point in time. h and f are assigned based on their value of x.
V = V(x,t) eta = eta(x,t) tau = tau(x,t) h = h(x), f = f(x) while g and rho are constants. The boundary values are V(0,0) = 0, eta(0,0)=0 , and tau(0,0) = 0. Assuming steady state conditions, the solution (V) is found by equating tau_sy and tau_by.

Answer 1

Ok, so here is a somewhat simple numerical scheme, that shows conceptual properties of your system. It is analogous to (explicit) Euler's method. It can be easily generalized to an analogous implicit Euler-like method.

You are given:

The functions h(x), f(x) , tau_sx(x, t), tau_sy(x, t) and tau_by(x, t)

The constants g and rho

You are looking for :

The functions V(x, t) and eta(x, t) that satisfy the pair of differential equations above.

To be able to find solutions to this problem, you need to be given:

V(x, 0) = V0(x) and eta(0, t) = eta0(t)

Assume your domain is [0, L] X [0, T], where x in [0, L] and t in [0, T]. Discretize the domain as follows: choose M and N positive integers and let dx = L / M and dt = T / N. Then consider only the finite set of points x = m dx and t = n dt for any integers m = 0, 1, ..., M and n = 0, 1, ..., N.

I am going to restrict all functions on the finite set of points defined above and use the following notation for an arbitrary function funct:

funct(x, t) = funct[m, n] and funct(x) = funct[m] for any x = m dx and t = n dt.

Then, the system of differential equations can be discretized as

g*(h[m] + eta[m,n])*(eta[m+1, n] - eta[m,n])/dx = f[m]*(h[m] + eta[m,n])*V[m,n] + tau_sx[m,n]/rho

(V[m, n+1] - V[m,n])/dt = (tau_sy[m,n] - tau_by[m,n])/(rho*(h[m] + eta[m,n]))

Solve for eta[m+1,n] and V[m,n+1]

eta[m+1,n] = eta[m,n] + f[m]*V[m,n]*dx/g + tau_sx[m,n]*dx/(g*rho*(h[m] + eta[m,n]))

V[m,n+1] = V[m,n] + (tau_sy[m,n] - tau_by[m,n])*dt/(rho*(h[m] + eta[m,n]))

For simplicity, I am going to abbreviate the right hand sides of the equations above as

eta[m+1,n] = F_eta(m, n, eta[m,n], V[m,n])

V[m,n+1] = F_V(m, n, eta[m,n], V[m,n])

that is, something like

def F_eta(m, n, eta[m,n], V[m,n]):
    return eta[m,n] + f[m]*V[m,n]*dx/g + tau_sx[m,n]*dx/(g*rho*(h[m] + eta[m,n]))

def F_V(m, n,  eta[m,n], V[m,n]):
    return V[m,n] + (tau_sy[m,n] - tau_by[m,n])*dt/(rho*(h[m] + eta[m,n]))

From the boundary conditions, we know

eta[0,n] = eta0[n] = eta0(n*dt) and

V[m,0] = V0[m] = V0(m*dx)

as input, for m = 0,..., M and n = 0,..., N.

for n in range(N):
    for m in range(M):
        eta[m+1,n] = F_eta(m, n, eta[m,n], V[m,n])
        V[m,n+1] = F_V(m, n, eta[m,n], V[m,n])

(you have to tweak these loops to reach the rightmost and the upper boundary points, but the philosophy stays the same)

Basically, you follow the pattern: generate the etas along the horizontal x axis and at the same time you generate a V one layer up. Then you move up to the next horizontal level.

o --eta--> o --eta--> o --eta--> o --eta--> o
|          |          |          |          | 
V          V          V          V          V
|          |          |          |          |
o --eta--> o --eta--> o --eta--> o --eta--> o