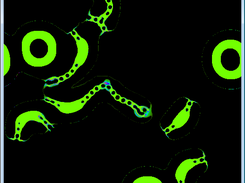
Conway's Game of Life is generalized to a continuous domain. OpenGL and GLSL shaders are used for real-time 2D and 3D graphics. Time stepping is done via a real to complex FFT based convolution operation. There are also two deliberately simple test implementations in FreeBasic and Matlab. A 2D version on a sphere shows that it is really not dependent on the underlying grid.

Features

  • 1D, 2D and 3D with various visualization choices
  • uses FFT for fast computation even for big neighborhoods
  • change parameters in real-time and watch the effect
  • parameters are saved and loaded easily, nothing is lost of your experiments
  • uses the GPU for maximum performance, float precision is sufficient
  • simple version in FreeBasic that should be transferable to any system or language
  • small version in Matlab that shows the concept very clearly
  • version on a sphere that proves the independence of the underlying grid
  • version using SDL, that is the same for Windows, Linux and Mac (only source)

Project Samples

the generic smooth glider sphere version (seams are gone in the newest version) 1D version mode 2 smooth time stepping gives nicer colors some stuff in smooth time stepping mode 3d version

Project Activity

See All Activity >

Categories

Fractal

License

GNU General Public License version 2.0 (GPLv2)

Follow SmoothLife

SmoothLife Web Site

You Might Also Like
A new approach to fast data transfer | IBM Aspera Icon
A new approach to fast data transfer | IBM Aspera

For organizations interested in a file transfer and streaming solution

IBM Aspera takes a different approach to tackling the challenges of big data movement over global WANs. Rather than optimize or accelerate data transfer, Aspera eliminates underlying bottlenecks by using a breakthrough transport technology that fully utilizes available network bandwidth to maximize speed and quickly scale up with no theoretical limit.
Learn More
Rate This Project
Login To Rate This Project

User Ratings

4.8 out of 5 stars
★★★★★
★★★★
★★★
★★
★
3
1
0
0
0
ease 1 of 5 2 of 5 3 of 5 4 of 5 5 of 5 0 / 5
features 1 of 5 2 of 5 3 of 5 4 of 5 5 of 5 0 / 5
design 1 of 5 2 of 5 3 of 5 4 of 5 5 of 5 0 / 5
support 1 of 5 2 of 5 3 of 5 4 of 5 5 of 5 0 / 5

User Reviews

Filter Reviews:
All
  • spacejockey123 Posted 2016-12-22
    Hi. The main smooth executable file work fine and its very interesting, but I can't seem to get the matlab code to work. Errors like 'Creating a string using double quotes is not supported. Use the string function.' Have you run into this problem before? Maybe from a newer version of Matlab
  • tfileme Posted 2013-05-12
    Smoothlife works perfectly.
    1 user found this review helpful.
  • bromagosa Posted 2012-10-10
    Great project! Any chance to get it running under GNU/Linux?
  • tim_hutton Posted 2012-10-09
    Amazingly good! The rules are astonishing. And with FFT for speed, this runs really fast, even in 3D.
Read more reviews >

Additional Project Details

Operating Systems

Windows

Intended Audience

Science/Research, Education, Advanced End Users, Developers, End Users/Desktop

Programming Language

MATLAB, C++, BASIC, GLSL (OpenGL Shading Language)

Related Categories

MATLAB Fractal Software, C++ Fractal Software, BASIC Fractal Software, GLSL (OpenGL Shading Language) Fractal Software

Registered

2012-02-23
Report inappropriate content