Teoria do campo cristalino

A teoria do campo cristalino (TCC ou CFT, do termo em inglês crystal field theory) descreve a quebra da degenerescência de orbitais, geralmente orbitais $d$ ou $f$, devido a um campo elétrico estático produzido por uma distribuição de carga circundante (ligantes da molécula ou do ânion). Essa teoria tem sido usada para descrever várias espectroscopias de compostos coordenados, em particular espectros ópticos (cores das espécies). A TCC justificar algumas propriedades magnéticas e visuais, além de entalpias de hidratação e geometrias espaciais de complexos de metais de transição, mas não busca descrever as ligações. Ela foi desenvolvido pelos físicos Hans Bethe e John Hasbrouck van Vleck na década de 1930. A teoria foi subsequentemente combinada com a teoria do orbital molecular para formar a teoria do campo ligante (TCL), mais realista e complexa, a qual aborda o processo de ligação química em complexos de metais de transição.

Visão geral da teoria do campo cristalino

De acordo com a teoria do campo cristalino, a interação entre um metal de transição e seus ligantes ocorre pela atração entre o cátion metálico e a carga negativa nos elétrons livres do ligante. A teoria é desenvolvida considerando as mudanças de energia dos cinco orbitais $d$ degenerados ao serem circundados por uma série de cargas pontuais — os ligantes —. Conforme um ligante se aproxima do íon metálico, seus elétrons ficam mais próximos de alguns dos orbitais $d$ do metal e mais distantes de outros, proporcionando uma degenerescência. Os elétrons nos orbitais $d$ e aqueles no ligante se repelem devido à repulsão entre cargas semelhantes. Com isso, os elétrons $d$ mais próximos dos ligantes terão uma energia mais alta do que aqueles mais distantes, o que resulta no desdobramento energético dos orbitais $d$. Esse desdobramento é afetado pelos seguintes fatores:

• a natureza do íon metálico.
• o estado de oxidação do metal. Um estado de oxidação mais alto leva a uma maior diferença em relação a um campo esférico.
• o arranjo dos ligantes ao redor do íon metálico.
• o número de coordenação do metal (ou seja, o número de átomos doadores de elétrons).
• a natureza dos ligantes que cercam o íon metálico. Quanto mais forte for o efeito dos ligantes, maior será a diferença entre os orbitais $d$ de alta e de baixa energia.

A geometria mais comum em complexos é a octaédrica, na qual seis ligantes formam os vértices de um octaedro ao redor do íon metálico. Na simetria octaédrica, os orbitais $d$ se dividem em dois conjuntos com uma diferença de energia $\Delta _{o}$ (o parâmetro de desdobramento do campo cristalino ou do campo ligante, também comumente denotado por $10Dq$ para dez vezes o "diferencial de quanta") de forma que os orbitais $d_{xy}$, $d_{xz}$ e $d_{yz}$ passam a ter menos energia e os orbitais $d_{z^{2}}$ e $d_{{x^{2}}-{y^{2}}}$, maior energia, porque o primeiro grupo, estando mais distante dos ligantes do que o último, experimenta menor repulsão. Os três orbitais de energia mais baixa são referidos como $t_{2g}$ e os dois orbitais de energia mais alta como $e_{g}$. Esses rótulos são baseados na teoria de simetria molecular: eles são os nomes das representações irredutíveis do grupo de pontos octaédricos, $O_{h}$. Os diagramas de energia orbital típicos são fornecidos abaixo na seção Spin alto e spin baixo.

Os complexos tetraédricos são o segundo tipo mais comum; neles, quatro ligantes formam um tetraedro ao redor do íon metálico. Em um desdobramento de campo cristalino tetraédrico, os orbitais $d$ se dividem em dois grupos, com uma diferença de energia $\Delta _{t}$. Os orbitais de energia mais baixa são $d_{z^{2}}$ e $d_{{x^{2}}-{y^{2}}}$, e os orbitais de energia mais alta são $d_{xy}$, $d_{xz}$ e $d_{yz}$ — ao contrário do caso octaédrico —. Além disso, uma vez que os elétrons do ligante na simetria tetraédrica não são orientados diretamente para os orbitais $d$, o desdobramento energético é menor do que no caso octaédrico. A geometrias quadrado planar e outras geometrias complexas também podem ser descritas pela TCC.

O tamanho da lacuna $\Delta$ entre os dois ou mais conjuntos de orbitais depende de vários fatores, incluindo os ligantes e a geometria do complexo. Alguns ligantes contribuem com um pequeno valor de $\Delta$, enquanto outros causam uma grande variação de energia. As razões para isso podem ser explicadas pela teoria do campo ligante. A série espectroquímica é uma lista empírica de ligantes ordenados pelo tamanho da divisão $\Delta$ causada por eles (de pequeno $\Delta$ a grande $\Delta$):

I⁻ < Br⁻ < S²⁻ < SCN⁻ (ligado a S) < Cl⁻ < NO₃⁻< N₃⁻ < F^– < OH^– < C₂O₄^2– < H₂O < NCS^– (ligado ao N) < CH₃CN < py < NH₃ < en < 2,2'-bipiridina < fen < NO₂^– < PPh₃ < CN^– < CO.

O estado de oxidação do metal também contribui para o tamanho de $\Delta$ entre os níveis de energia alto e baixo. À medida que o estado de oxidação aumenta para um determinado metal, a magnitude de $\Delta$ aumenta. Um complexo V³⁺ terá um $\Delta$ maior do que um complexo V²⁺ para um determinado conjunto de ligantes, pois a diferença na densidade de carga permite que os ligantes estejam mais próximos de um íon V³⁺ do que de um íon V²⁺. A distância menor entre o ligante e o íon metálico resulta em um $\Delta$ maior, porque o ligante e os elétrons metálicos estão mais próximos e, portanto, se repelem mais.

Spin alto e spin baixo

Diagrama de campo cristalino do [Fe(NO₂)₆]^3–, de baixo spin

Os ligantes que causam um grande desdobramento $\Delta$ dos orbitais $d$ são referidos como ligantes de campo forte, tais como CN^– e CO — da série espectroquímica —. Em complexos com esses ligantes, é desfavorável que elétrons ocupem orbitais de alta energia. Portanto, os orbitais de energia inferior são completamente preenchidos antes que os superiores começem a ser ocupados, de acordo com o princípio de Aufbau. Complexos como este são referidos como "de spin baixo". Por exemplo, NO₂^– é um ligante de campo forte e leva a um grande $\Delta$. O íon octaédrico [Fe(NO₂)₆]³⁻, que tem 5 elétrons de orbitais $d$, teria o diagrama de divisão octaédrico mostrado à direita com todos os cinco elétrons no nível $t_{2g}$. Este estado de spin baixo, portanto, não segue a regra de Hund.

Diagrama de campo cristalino do [FeBr₆]^3–, de spin alto

Por outro lado, ligantes que causam um pequeno desdobramento $\Delta$ dos orbitais $d$, como I^– e Br^–, são referidos como ligantes de campo fraco. Nesse caso, é mais estável a ocupação tanto de orbitais de maior energia como de menor energia em vez de dois elétrons no mesmo orbital de baixa energia, visto que eles sofrem repulsão entre si. Assim, um elétron é colocado em cada um dos cinco orbitais $d$ segundo a regra de Hund e complexos de "spin alto" são formados antes que ocorra qualquer emparelhamento. Por exemplo, Br^– é um ligante de campo fraco e produz um pequeno $\Delta _{o}$. Assim, o íon [FeBr₆]³⁻, novamente com cinco elétrons de orbitais $d$, teria um diagrama de divisão octaédrico na qual cada um dos 5 orbitais.

Para que ocorra o preenchimento de spin baixo, o custo energético do preenchimento de um orbital previamente semipreenchido deve ser menor que aquele de pôr o elétron adicional em um orbital $e_{g}$ a um custo de energia de $\Delta$. Conforme observado acima, $e_{g}$ refere-se aos orbitais $d_{z^{2}}$ e $d_{{x^{2}}-{y^{2}}}$ (para complexos octaédricos), que são mais elevados em energia do que $t_{2g}$. Se a energia necessária para emparelhar dois elétrons é maior que $\Delta$ — o custo energético de colocar um elétron em um orbital $e_{g}$ —, ocorre a formação de um complexo de spin alto.

O parâmetro de desdobramento do campo cristalino para complexos tetraédricos é denotado por $\Delta _{t}$ e é aproximadamente igual a ${\frac {4}{9}}$ $\Delta _{o}$ (para o mesmo metal e os mesmos ligantes). Portanto, a energia necessária para emparelhar dois elétrons é normalmente maior do que a energia necessária para pôr os elétrons nos orbitais de maior energia, sendo os complexos tetraédricos geralmente de spin alto.

O uso desses diagramas de divisão pode auxiliar na previsão das propriedades magnéticas de compostos de coordenação. Um composto que tem elétrons desemparelhados em seu diagrama de divisão será paramagnético e será atraído por campos magnéticos, enquanto um composto que não tiver elétrons desemparelhados em seu diagrama de divisão será diamagnético e fracamente repelido por um campo magnético.

Energia de estabilização do campo cristalino

A energia de estabilização do campo cristalino (EECC ou CFSE, do termo em inglês crystal field stabilization energy) é a energia de estabilidade reduzida que resulta da inserção de um íon de metal de transição no campo cristalino gerado por um conjunto de ligantes. Ela surge devido ao fato de que, quando os orbitais $d$ são desdobrados em um campo de ligantes (como descrito acima), alguns deles se tornam menos energéticos que antes em relação a um campo esférico — cuja variação de energia é conhecida por baricentro — no qual todos os cinco orbitais $d$ são degenerados. Por exemplo, em um caso octaédrico, o conjunto de orbitais $t_{2g}$ torna-se menor em energia do que os orbitais no baricentro. Como resultado disso, se houver algum elétron ocupando esses orbitais, o íon metálico é mais estável no campo do ligante em relação ao baricentro por uma quantidade conhecida como EECC. Por outro lado, os orbitais $e_{g}$ no caso octaédrico, são mais energéticos em relação ao baricentro, causando a sua ocupação uma redução da EECC.

Energia de estabilização do campo cristalino octaédrico. Orbitais atômicos $d$ degenerados de um íon metálico livre (à esquerda), desestabilização de orbitais $d$ dentro de um campo elétrico esférico negativo (ao centro) e perda de degeneração em relação ao campo esférico quando os ligantes são tratados como cargas pontuais em uma geometria octaédrica (à esquerda).

Se a separação dos orbitais $d$ num campo octaédrico é $\Delta _{o}$, os três orbitais $t_{2g}$ são estabilizados em relação ao baricentro por ${\frac {2}{5}}\Delta _{o}$ e os orbitais $e_{g}$ são desestabilizadas por ${\frac {3}{5}}\Delta _{o}$. Como exemplos, considere-se as duas configurações $d^{5}$ mostradas mais adiante na página. O caso de spin baixo (superior) tem cinco elétrons nos orbitais $t_{2g}$, de modo que a EECC total é de $5\times {\frac {2}{5}}\Delta _{o}$ = $2\Delta _{o}$. No caso de spin alto (inferior), a EECC é ${\bigg (}3\times {\frac {2}{5}}\Delta _{o}{\bigg )}-{\bigg (}2\times {\frac {3}{5}}\Delta _{o}{\bigg )}=0$ (caso em que a estabilização gerada pelos elétrons nos orbitais mais baixos é anulada pelo efeito desestabilizador dos elétrons nos orbitais superiores).

Propriedades ópticas

As propriedades ópticas (detalhes dos espectros de absorção e de emissão) de muitos complexos de coordenação podem ser explicadas pela teoria do campo cristalino. Frequentemente, entretanto, as cores mais intensas dos complexos metálicos surgem de excitações de transferência de carga mais intensas.

Gemoetrias e diagramas de desdobramento de campo cristalino

Nome	Forma	Diagrama energético
Octaédrica
Bipirâmide pentagonal
Antiprismática quadrada
Quadrado planar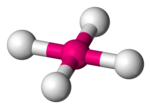
Pirâmide de base quadrada
Tetraédrica
Bipirâmide trigonal

Ver também

• Teoria do orbital molecular

Leitura adicional

• Miessler, G. L.; Tarr, D. A. (2003). Inorganic Chemistry 3rd ed. [S.l.]: Pearson Prentice Hall. ISBN 978-0-13-035471-6 
• Orgel, Leslie E. (1960). An introduction to transition-metal chemistry: Ligand-Field theory. [S.l.]: Methuen. ISBN 978-0416634402 
• Shriver, D. F.; Atkins, P. W. (2001). Inorganic Chemistry 4th ed. [S.l.]: Oxford University Press. pp. 227–236. ISBN 978-0-8412-3849-7 
• Silberberg, Martin S (2006). Chemistry: The Molecular Nature of Matter and Change 4th ed. [S.l.]: New York: McGraw Hill Company. pp. 1028–1034. ISBN 978-0-8151-8505-5 
• Zumdahl, Steven S (2005). Chemical Principles 5th ed. [S.l.]: Houghton Mifflin Company. pp. 550–551, 957–964. ISBN 978-0-669-39321-7 

Ligações externas

• Crystal-field Theory, Tight-binding Method and Jahn-Teller Effect in E. Pavarini, E. Koch, F. Anders e M. Jarrell (eds. ): Correlated Electrons: From Models to Materials, Jülich 2012,ISBN 978-3-89336-796-2
• Crystal field theory (draft article) em Citizendium.org