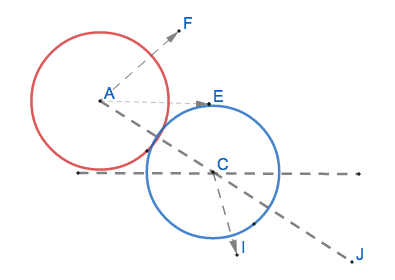
Two spherical bodies of mass $m_1$ and $m_2$ are placed in gravity free space as shown. Initially, the body with mass $m_2$ is at rest and the body with mass $m_1$ approaches the other body with a velocity $u \hat{i}$. An elastic oblique collision occurs. Find the ratio $\frac{m_1}{m_2}$ such that the maximum angle of deflection of $m_1$ is $60^\circ$.
I decided to solve this in the lab frame (or call it the ground frame), and I can't proceed until I know atleast one more parameter. If I solve it in the frame of the mass centre, as you will later see, it will be quite trivial. Can someone help m solve it in the ground frame?
My solution in the lab frame: Let $\angle{EAC} = \phi$, $\angle{JCI}= \beta$ and $\angle{FAE} = \alpha$ (see figure). In the collision, the impulse provided by contact force during collision is nearly zero and hence momentum can be conserved along the line of collision AC. Let $v_1$ be the speed if the body with mass $m_1$ after collision (at an angle of $\alpha$ with horizontal) and $v_2$ be speed of the body with mass $m_2$ after collision (at an angle of $\beta$ with the line of collision). Using conservation of momentum along line of collision, $$m_1 u \cos{\phi} = m_1 v_1 \cos{(\phi +\alpha)} + m_2 v_2 \cos{\beta}$$ Since the collision is elastic, $$e = 1 = \frac{v_2 \cos{\beta} - v_1 \cos{(\phi +\alpha)}}{u \cos{\phi} - 0}$$ Solving these two equations, we get $$\frac{(\frac{m_1}{m_2} +1)}{(\frac{m_1}{m_2} - 1)} \cdot \frac{v_1}{u} = \frac{\cos{\phi}}{\cos{(\phi + \alpha)}}$$ Let $\frac{m_1}{m_2} = \kappa$, now we use the fact that no motion is affected along the line perpendicular to the line of collision. So $\frac{v_1}{u} = \frac{\sin{\phi}}{\sin{(\phi+\alpha)}}$ and putting this in the expression we had got from the first two equations, we get $$\kappa = \frac{\tan{(\phi+\alpha)}+\tan{\phi}}{\tan{(\phi+\alpha)} - \tan{\phi}}$$ Now we need to find $\kappa$ such that the maximum angle of deflection of $m_1$ is $60^\circ$, which is equivalent to saying that $\tan{\alpha} \leq \sqrt{3}$. Just using the boundary condition of $\tan{\alpha} = \sqrt{3}$ should yield the result. This gives us the quadratic equation $$\kappa = 1+\frac{2}{\sqrt{3} (\cot{\phi} - \tan{\phi})}$$ which should be the desired answer.
But the problems with this result are 1) the maximum value of angle deflection is $\phi$ dependent, or dependent on the shape of the bodies, and 2) $\phi$ is an unknown and 3) it is not the correct answer. Is there some way in which we can calculate the numerical value of $\kappa$ in the ground frame, irrespective of any unknown parameters? And can someone point out the errors in this solution?
A hint for solving in the CM frame: Solving this problem in the frame of the centre of mass is quite beautiful. Here's a line of thought that'll lead to the answer: Use this well known fact- In elastic collisions, momentum vectors of the colliding bodies initially and finally are equal and opposite! (Try proving it as well, and try to think what'll happen in a general collision.) This would lead us to the conclusion that the speeds of the two bodies will remain same after collision in the frame of mass centre. So $\sin{\phi_{\text{max}}} = \frac{v_{\text{1, CM}}}{v_{\text{CM}}}$. Now it should be trivial from here. ;)