I have come across a few situations involving leaking and loading freight cars being pushed with a constant force. Here, I present two situations that leave me in doubt.
1) A car of mass $M_0$( sand of mass $m$ included ) at rest experiences a constant force $F$ at $t=0$ and starts to leak from the bottom at a constant rate $b$ at the same time. I am to calculate its speed when all the sand leaks out.
Here, I am concerned with the system's horizontal momentum.
I have, $P(0) = 0$ and $P(t) = (M_0 - m)v + x $, where $t$ is the time taken for all the sand to leak out, $v$ is the speed attained by the car at $t$ and $x$ is the momentum of the escaped sand subsystem.
Since the mass of the system remains unchanged, I have, $\Delta P = (M_0 - m)v + x = \int_{0}^{t} F \mathrm dt$
I do not see myself in a position to calculate $x$, and that is why I'm not sure if this approach is correct. While I do know the solution to this question( a different approach ), I would like to know if there are any flaws with my reasoning here. Can I expect the right answer if $x$ is correctly known?
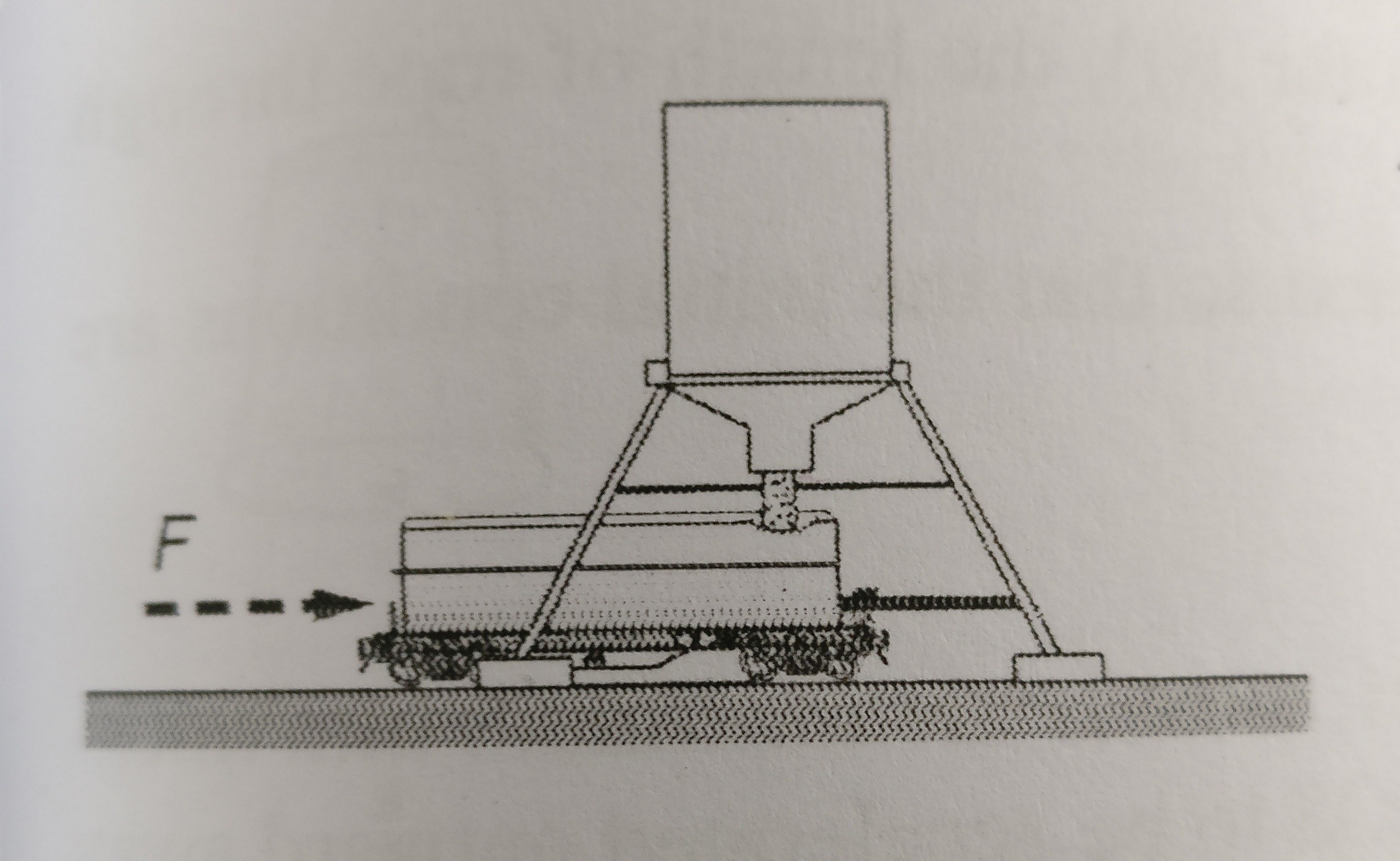
The next question concerns the loading of a freight car.
2) A freight car of mass $M$ starts from rest under an applied force $F$. At the same time, sand begins to run into the car at a steady rate $b$ from a hopper at rest along the track. I am to calculate its speed when a mass $m$ of sand has been transferred.
Once again, I'm concerned with the system's$( M + m )$ horizontal momentum. I am given, $\frac{\mathrm d M_{\mathrm car}}{\mathrm dt} =b$. Mass of the freight car at any time $t$ is then found out to be $M + bt$.
At some time $t$ I have, $P(t) = (M + bt) v$, where $v$ is the speed at that time.
Sometime later, $P(t+\Delta t) = (M + bt + b\Delta t) (v + \Delta v)$
The average rate of change of momentum is given by, $ \frac{\Delta P}{\Delta t} = ( M + bt) \frac{\Delta v}{\Delta t} + b( v + \Delta v) $
When I take $\Delta t \rightarrow 0 $, I see that the net external force depends on the speed of the car. This is an absurd result because if I shift my origin from my current inertial frame to another inertial frame( moving with a different speed ), the force acting on the car will be different. This is not possible. Where could I have gone wrong with my reasoning? The solution to this question is simple. However, I am curious to know where I went wrong.