Sum of normal forces

Question

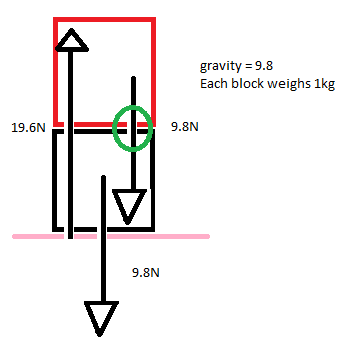
For the red block to not go through the black block the black block needs to push the red block with equal force(normal force) or else it will go through the black block, but where is the normal force? How can the sum of the black and red blocks force be equal to the normal force of the pink surface when the force of the red block is nulled by the normal force of the black block? In the picture I drew a green circle where the normal force between the black and red block "should be". Any explanation?

Answer 1

The reason is that the normal force acts on two different bodies.

The upper block pushes the black box down with its weight and the black box provides the normal force to the red box so that the net force on the red box becomes 0 but these two forces (normal force due to black box and the weight of red box) act on two different bodies, so they cannot cancel each other out.

The force due to the red box (it's weight)adds to the weight of the black box. So now the ground has to provide the black box the normal force equal to the weight of both the boxes.

Answer 2

Consider both the blocks as one system. Thus the system mass is 2kg and the normal force applied by earth surface to this system is therefore 19.6N to satisfy the equilibrium. Other normal forces are just internal.