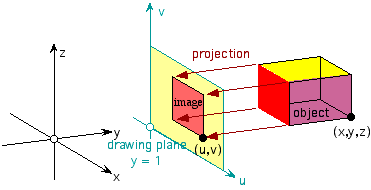
This tag is for questions relating to "Projection", which is nothing but the shadow cast by an object. An everyday example of a projection is the casting of shadows onto a plane. Projection has many application in various areas of Mathematics (such as Euclidean geometry, linear algebra, topology, category theory, set theory etc.) as well as Physics.
The concept of projection in mathematics is a very old one, most likely has its roots in the phenomenon of the shadows cast by real-world objects on the ground. Originally, the notion of projection was introduced in Euclidean geometry to denote the projection of the Euclidean space of three dimensions onto a plane in it.
Type I: In plane projections, a series of points on one plane may be projected onto a second plane by choosing any focal point, or origin, and constructing lines from that origin that pass through the points on the first plane and impinge upon the second. This type of mapping is called a central projection.
The figures made to correspond by the projection are said to be in perspective, and the image is called a projection of the original figure. If the rays are parallel instead, the projection is likewise called parallel; if, in addition, the rays are perpendicular to the plane upon which the original figure is projected, the projection is called orthogonal. If the two planes are parallel, then the configurations of points will be identical; otherwise this will not be true.
Type II: A second common type of projection is called stereographic projection. It refers to the projection of points from a sphere to a plane. This may be accomplished most simply by choosing a plane through the centre of the sphere and projecting the points on its surface along normals, or perpendicular lines, to that plane.
In general, however, projection is possible regardless of the attitude of the plane. Mathematically, it is said that the points on the sphere are mapped onto the plane; if a one-to-one correspondence of points exists, then the map is called conformal.
- In an abstract setting we can generally say that, a projection is a mapping of a set (or other mathematical structure) into a subset (or sub-structure), which is equal to its square for mapping composition (or, in other words, which is idempotent).
The restriction to a subspace of a projection is also called a projection, even if the idempotence property is lost.
References: