Help identify 16-bit PRNG algorithm

Question

I am trying to identify a 16-bit PRNG for which I have the whole sequence (period is 51445).

So far I have managed to identify that the algorithm does a bit swapping followed by an XOR:

def prng(seed: int):
    s = fun1(seed) # Shift size, mapping not identified
    xor = fun2(seed) # XOR code, mapping not identified
    
    seed = ((seed << s) | (seed >> (16-s))) & 0xFFFF

    if seed & 1:
        seed ^= xor

    return seed

For s=1 and xor = 0x2C, the above algorithm produces the correct result for about 43k seeds (85%). I am currently working on finding a mapping for the shift size (defined by fun1() in the code above).

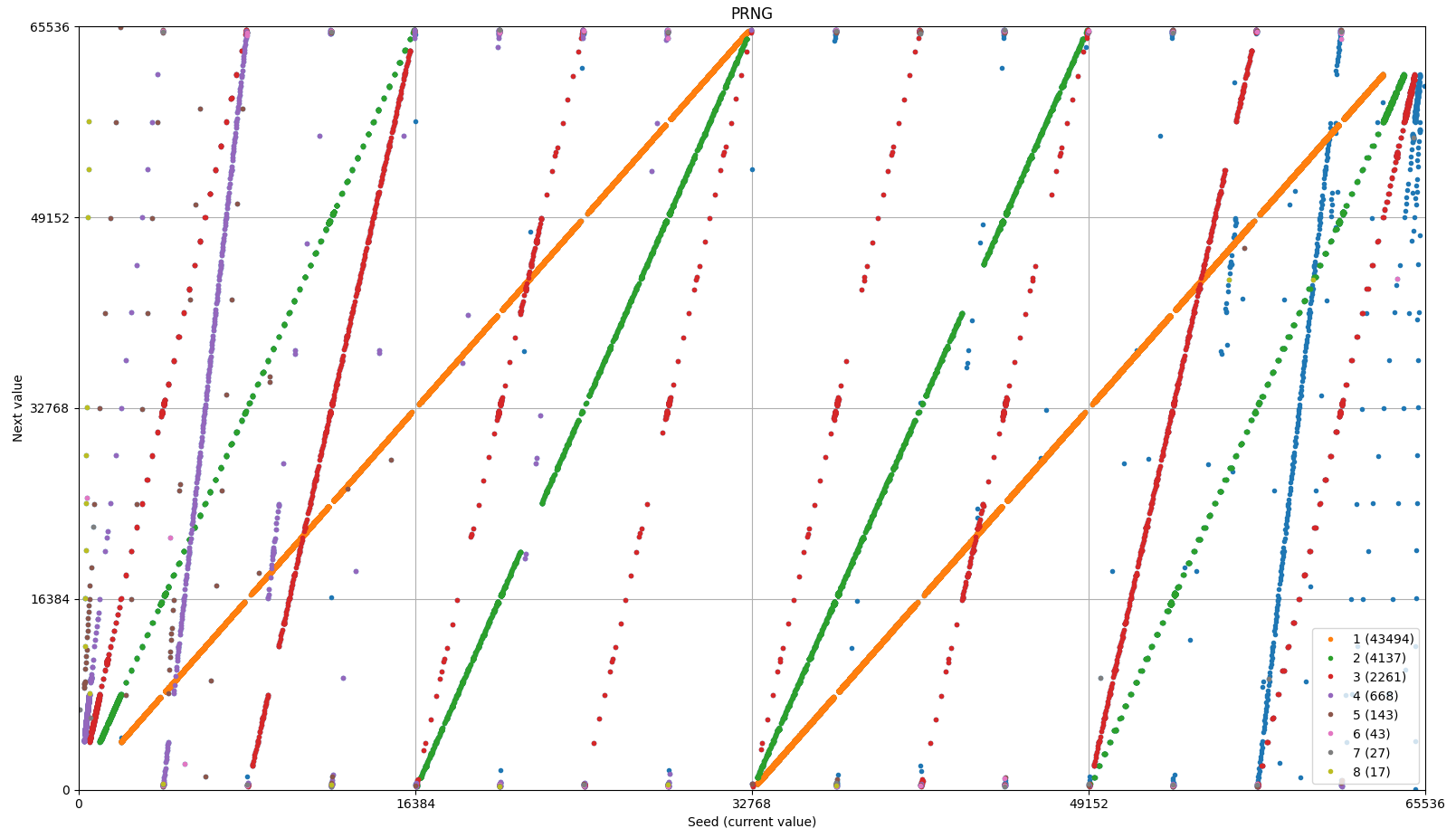
Here is the plot of the shift size for each seed. As can be seen from the legend, the shift size s=1 is identified for 43494 seeds, s=2 for 4137 seeds etc. What is particularly interesting is that the graph seems to be symmetric wrt. the point (32768, 32768).

I do not think the solution for this is in simple polynomials. Here is an excerpt of shift size vs. seed for some seed values (the first column is shift size, and everything else is the seed in different bases). For a very small change in bit structure (bit flip at position 4), the shift size changes significantly.

What I'm asking is for help with identifying the fun1() - any idea is welcome!

P.S. If it helps, the PRNG algorithm in question is implemented in a 20+ years old Zilog microcontroller (CLEP 2.1).

-    56544    DCE0    1101 1100 1110 0000
2    56545    DCE1    1101 1100 1110 0001
2    56546    DCE2    1101 1100 1110 0010
2    56547    DCE3    1101 1100 1110 0011
3    56548    DCE4    1101 1100 1110 0100
3    56549    DCE5    1101 1100 1110 0101
3    56550    DCE6    1101 1100 1110 0110
3    56551    DCE7    1101 1100 1110 0111
1    56552    DCE8    1101 1100 1110 1000
1    56553    DCE9    1101 1100 1110 1001
1    56554    DCEA    1101 1100 1110 1010
3    56555    DCEB    1101 1100 1110 1011
1    56556    DCEC    1101 1100 1110 1100
1    56557    DCED    1101 1100 1110 1101
1    56558    DCEE    1101 1100 1110 1110
1    56559    DCEF    1101 1100 1110 1111

1    56560    DCF0    1101 1100 1111 0000
1    56561    DCF1    1101 1100 1111 0001
1    56562    DCF2    1101 1100 1111 0010
1    56563    DCF3    1101 1100 1111 0011
1    56564    DCF4    1101 1100 1111 0100
1    56565    DCF5    1101 1100 1111 0101
1    56566    DCF6    1101 1100 1111 0110
1    56567    DCF7    1101 1100 1111 0111
1    56568    DCF8    1101 1100 1111 1000
1    56569    DCF9    1101 1100 1111 1001
1    56570    DCFA    1101 1100 1111 1010
-    56571    DCFB    1101 1100 1111 1011
1    56572    DCFC    1101 1100 1111 1100
1    56573    DCFD    1101 1100 1111 1101
1    56574    DCFE    1101 1100 1111 1110
1    56575    DCFF    1101 1100 1111 1111