Struggling to find an angle.

Question

As the figure below shows, two triangles $ABC$ and $ACD$ are overlapping.
The question is asking what the value of angle $B$ is.
I drew the figure in $GeoGebra$ and found out that $AB=AC$ which means the triangle $ABC$ is an isosceles triangle and therefore the angle $B=78°$.
And now I'm stuck at this point and I don't know whether I have to prove that the triangle $ABC$ is an isosceles triangle or I have to try some other ways to find the value of angle $B$.
Any help is highly appreciated.

Answer 1

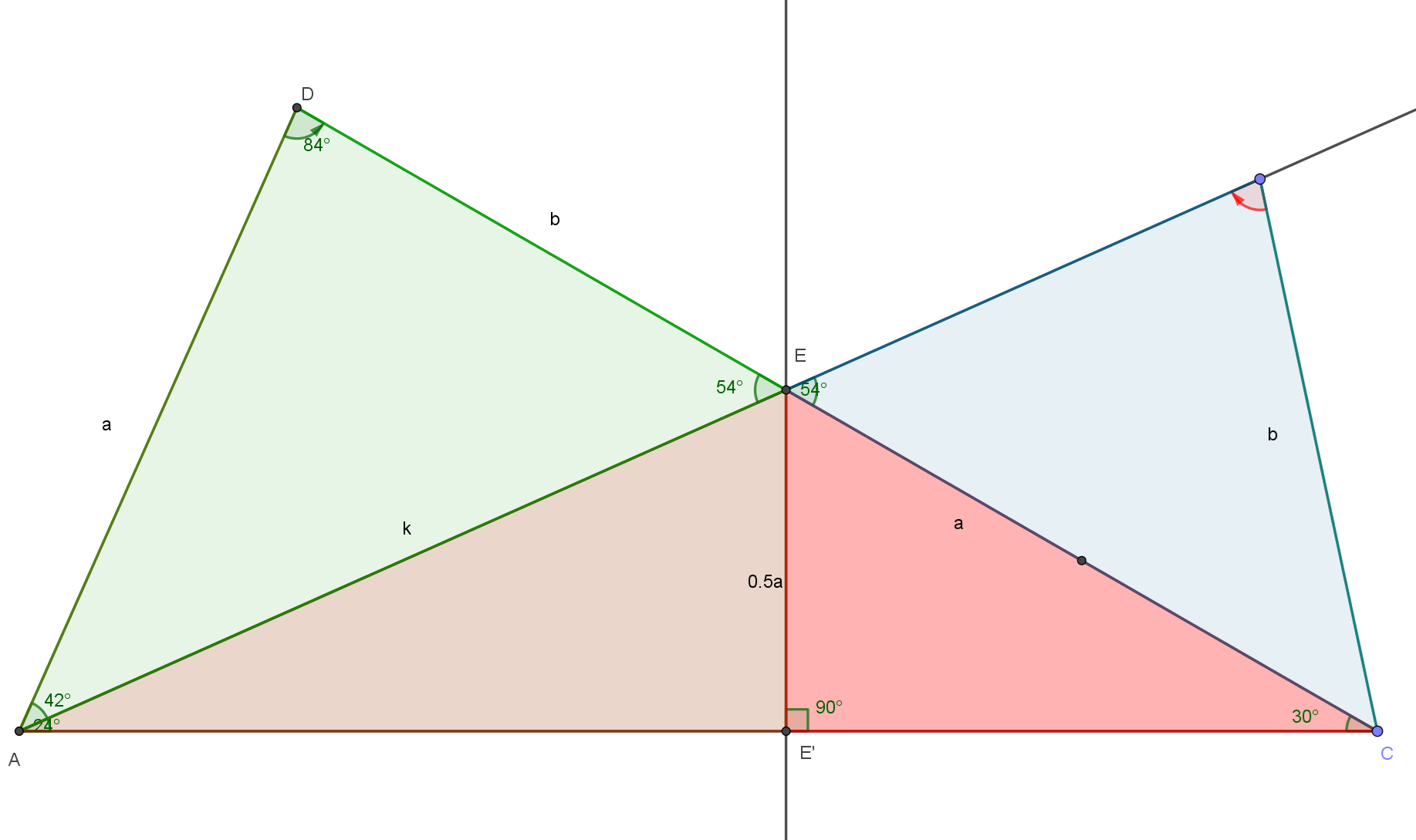
Draw E’ on AC such that EE’ is perpendicular to AC.

In the red triangle, EE’ = 0.5a.

From the brown triangle, obtain k as a function of a.

From the green triangle, find (1) $\angle D$; (2) $\angle DAE$; (3) the ratio of a: b.

From the blue triangle, get a : b in terms of the required unknown angle.

Equate the two a : b ratios. Eliminate　a：ｂ　to get $\angle B$

Answer 2

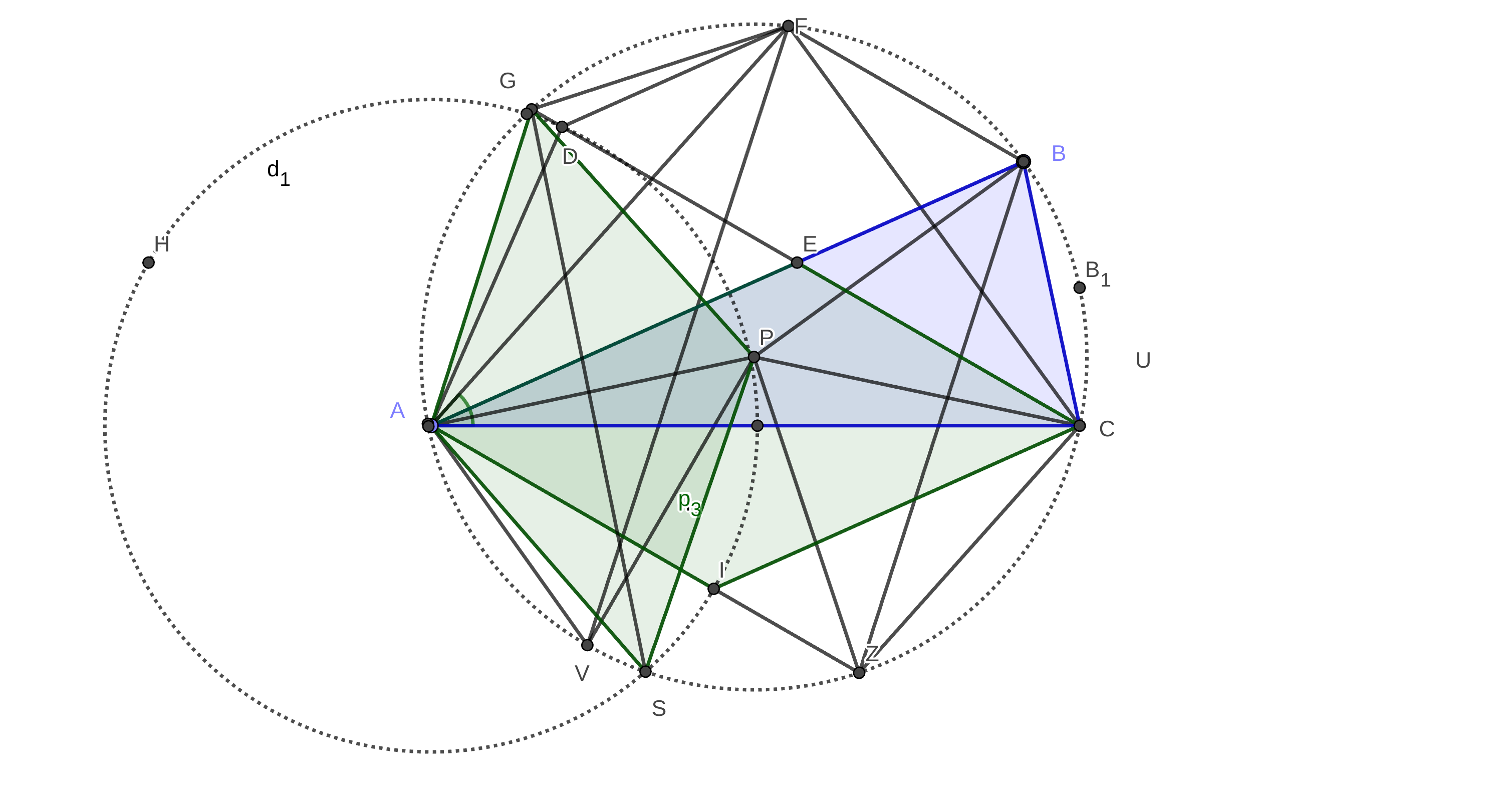
In figure we have:

$\overset{\large \frown}{CB}=48^o$

$\overset{\large \frown}{AG}=60^o$

$CG||BF\Rightarrow \overset{\large \frown}{GF}=48^o$

$CE=AI=AG=AS$

Because $\overset{\large \frown}{AG}=60^o$

Also:

$AZ||GC\Rightarrow \overset{\large \frown}{CZ}=\overset{\large \frown}{AG}=60^o$

$BZ||FV\Rightarrow \overset{\large \frown}{BF}=\overset{\large \frown}{VZ}$

so we have following sum of arcs:

$BC+BF+GF+AG+AV+VZ+ZC=360^o$

$VZ=BF$

$AV=GF=48^o$

So we have:

48+48+60+48+2BF+60=360

Which results in:

$2BF=240-3\times 48=96\Rightarrow BF=48$

$\Rightarrow AC=AV+VZ+ZC=48+48+60=156$

$\Rightarrow \angle ABC=\frac{\overset{\large \frown}{AC}=156^o}2=78^o$

Answer 3

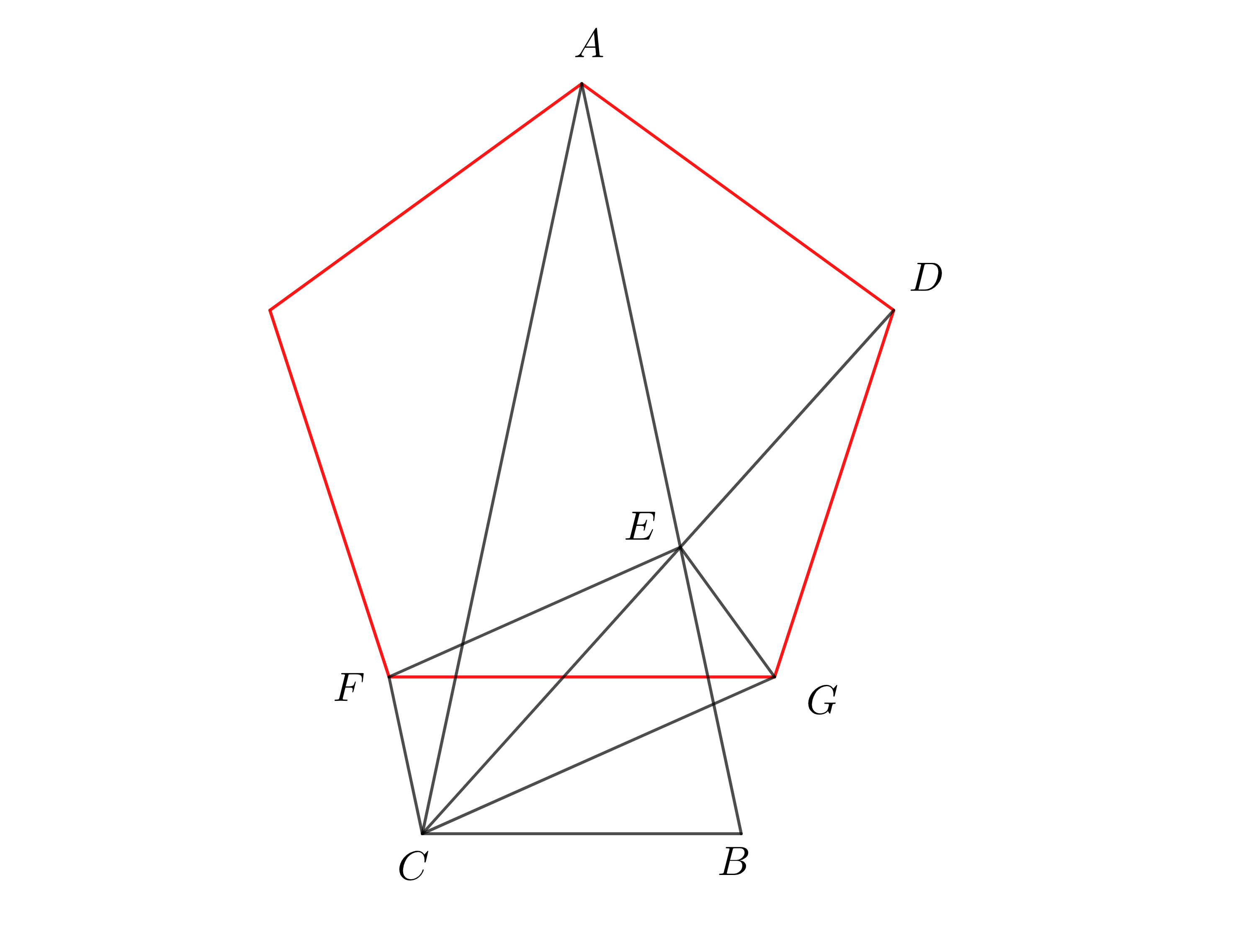
Just a HINT, I could not work out the entire path. But I thought it could be interesting to share the fact that the figure can be constructed with a regular pentagon and some isosceles triangles. In particular, $FGC$ and $GCD$ are isosceles. If you can show that also $CEG$ is isosceles, then you get that $AD \cong CE$ as desired. Once this is done, it is easy to prove that $EF\cong BC\cong ED$.

Answer 4

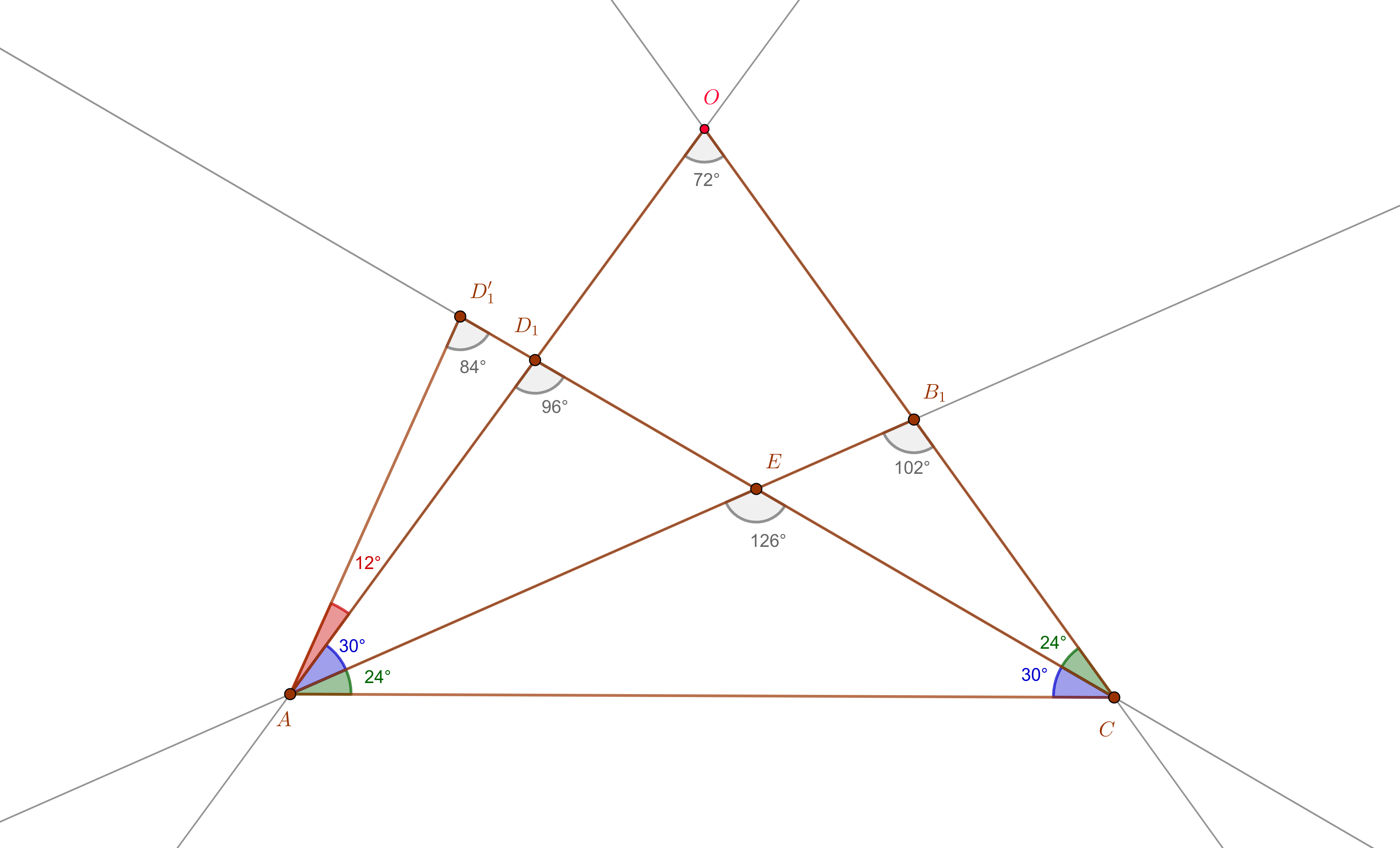
First of all, observe that there are two positions of the point $B$, below in the picture $B$ and $B_1$, so that the figure is "matched as is". With the restriction that the angle in $B$ in $\Delta ABC$ is acute we have only one possible position. But both points have some geometric meaning, so let us first find a path to uniquely construct the given constellation of points with an acute $\hat B$. This is done in a first part $(1)$ for the sake of completeness.

In a second part $(2)$ we have a first short solution involving trigonometry, at least the shortest i could find.

In a last third part $(3)$ i am trying to give a short synthetic proof based on a regular $30$-gon. It is not short enough for some taste (including mine), but there is also a time limit for searching for a shorter one. The interested reader may do this with similar ideas and a further smart observation, then please post an answer.

---

---

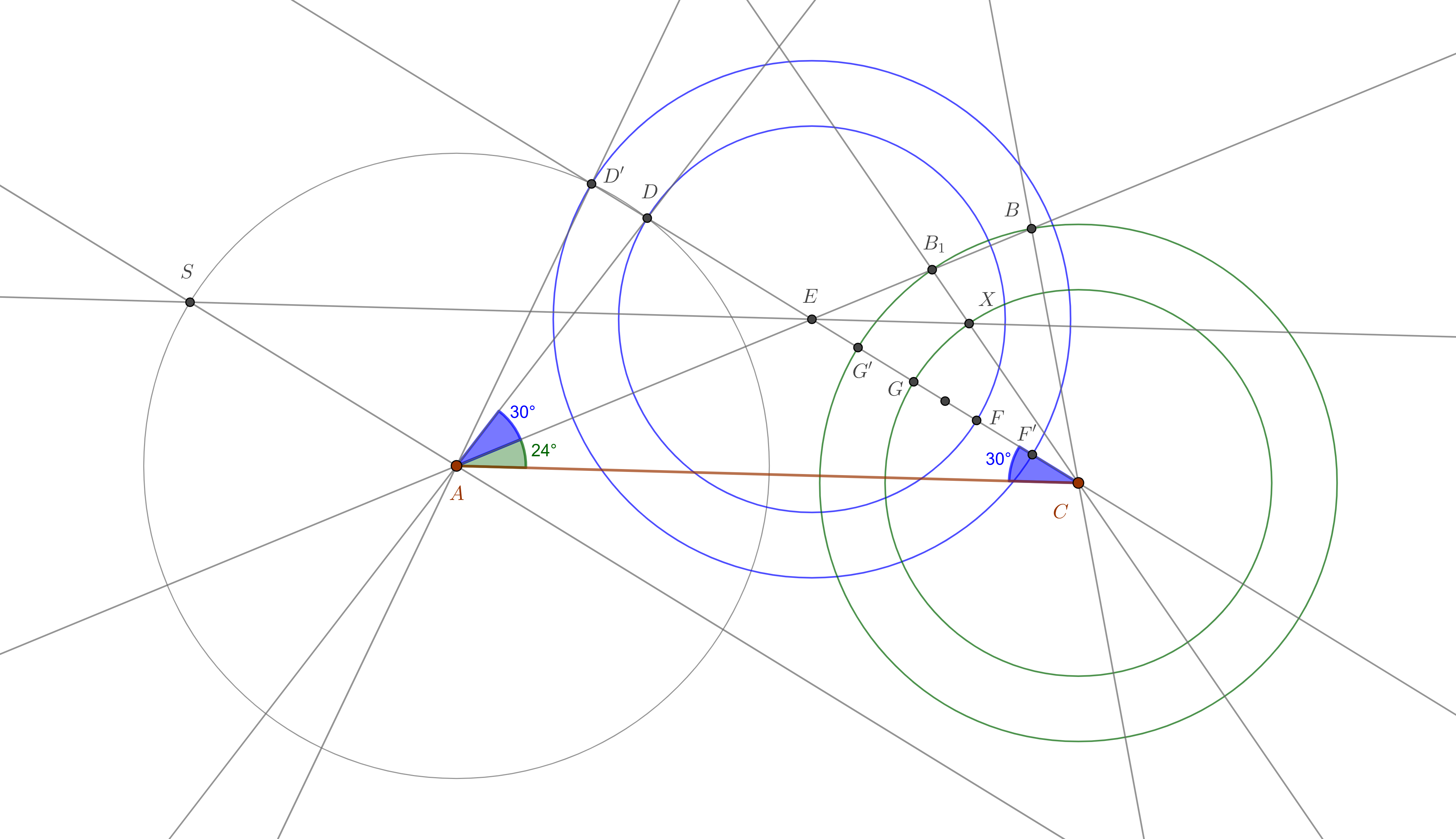
$(1)$ Discussion about the uniqueness of the given constellation of points:

We start with an arbitrary segment $AC$, and construct the angles of $24^\circ$ in $A$ and of $30^\circ$ in $C$ in the same (upper) half-plane. The corresponding rays intersect in $E$. We construct the parallelogram $ACES$, so transfer $CE$ as a segment $AS=CE$ with a vertex in $A$. We draw the circle centered in $A$ with radius $AS$, it intersects the ray $CE$ in two points, denoted by $D,D'$. (To fix the notation, $D$ is between $D'$ and $E$.) Let $F,F'$ be the reflections of $D,D'$ w.r.t. the point $E$. Let $G,G'$ be the reflections of $F,F'$ w.r.t. the mid point of $CE$. In this manner, we have segments of wanted lengths with a vertex in $C$, they are $CG=EF=ED$, and $CG'=EF'=ED'$. (Blue concentric circles show which segments were moved from one side of $E$ to the other side on the line $CE$.) We draw green circles centered in $C$ with radius $CG$, respectively $CG'$. It turns out that the smaller circle is not intersecting $AE$, so leads to no wanted constellation of points. However, the green circle with radius $CG'$ intersects $AE$ in two points $B,B_1$. We choose $B$ to be the point which has a bigger distance to $A$ and $E$. In a picture:

In the geogebra picture it turns out that the angle $\widehat {CAD}$ is a $30^\circ$-angle, as in $C$ in $\Delta EAC$. And the angle $\widehat {B_1CE}$ is a $24^\circ$-angle, as in $A$ in $\Delta EAC$. Similar triangles appear in the picture in a natural way: $\Delta ACD\sim \Delta EAD$, $\Delta ACB_1\sim \Delta CEB_1$, but of course, we have to show such properties. In such situations, i am taking the most generous symmetric constellation of points that may cover more (in best case) all important needed points.

---

---

$(2)$ First solution:

We try to use these "coincidences" as a hint. We use in a first solution $D_1$ instead of $D$, introduced in an alternative manner, till we have a match $D_1=D$.

The trigonometric solution needs a short lemma:

Short Lemma: We have: $$ 0 = 1+2\cos 72^\circ-2\cos 36^\circ\ . $$ Proof: Consider in the complex plane the regular pentagon centered at zero with $1$ as one of its vertices. Then the other four vertices project on the $x$ axis in $\cos 72^\circ$ (two) and $\cos 144^\circ=-\cos 36^\circ$ (the remained two). Since zero is the centroid, we have the wanted relation.

$\square$

Trigonometric solution: Let $\Delta EAC$ be the triangle with angles $\hat E,\hat A,\hat C$ having measures $126^\circ$, $24^\circ$, $30^\circ$. Construct points

• $D_1$ on the ray $[CE$, so that $\widehat{D_1AE}=30^\circ$, and
• $B_1$ on the ray $[AE$, with $\widehat{B_1CE}=24^\circ$.

Let $D_1'\ne D_1$ be the other point on $CE$ with $AD_1=AD_1'$. Then we have:

$$ \begin{aligned} \frac{CE}{AD_1} &= \frac{AC}{AD_1}\cdot \frac{CE}{AC} = \frac{\sin 96^\circ}{\sin 30^\circ}\cdot \frac{\sin 24^\circ}{\sin 126^\circ} = \frac{2\sin 96^\circ\sin 24^\circ}{\cos 36^\circ} \\ &= \frac{\cos (96^\circ- 24^\circ)-\cos (96^\circ+ 24^\circ)}{\cos 36^\circ} = \frac{\cos 72^\circ +\frac 12}{\cos 36^\circ}=1 \ , \\ &\qquad\text{ so we have $AD_1=AD_1'=CE$,} \\[3mm] \frac{D_1'E}{CB_1} &= \frac{D_1'E}{D_1'A} \cdot \frac{CE}{CB_1} = \frac{\sin 42^\circ}{\sin 54^\circ}\cdot \frac{\sin 102^\circ}{\sin 54^\circ} \\ &=\frac{\cos(102^\circ-42^\circ)-\cos(102^\circ+42^\circ)} {1-\cos 108^\circ} =\frac{\frac 12+\cos36^\circ} {1+\cos 72^\circ}=1\ , \\ &\qquad\text{ so we also have $D_1'E=CB_1$.} \end{aligned} $$ In both cases we have used the short lemma. So the point $B$ from the problem is located either in the constructed point $B_1$, with a corresponding angle $\widehat{AB_1C=102^\circ}$, or in the other location $B\in [AE$ (with $\Delta CBB_1$ isosceles) with a corresponding angle $\widehat{ABC=180^\circ-102^\circ=78^\circ}$.

$\square$

This is a simple complete solution using trigonometry.

---

---

$(3)$ Second solution:

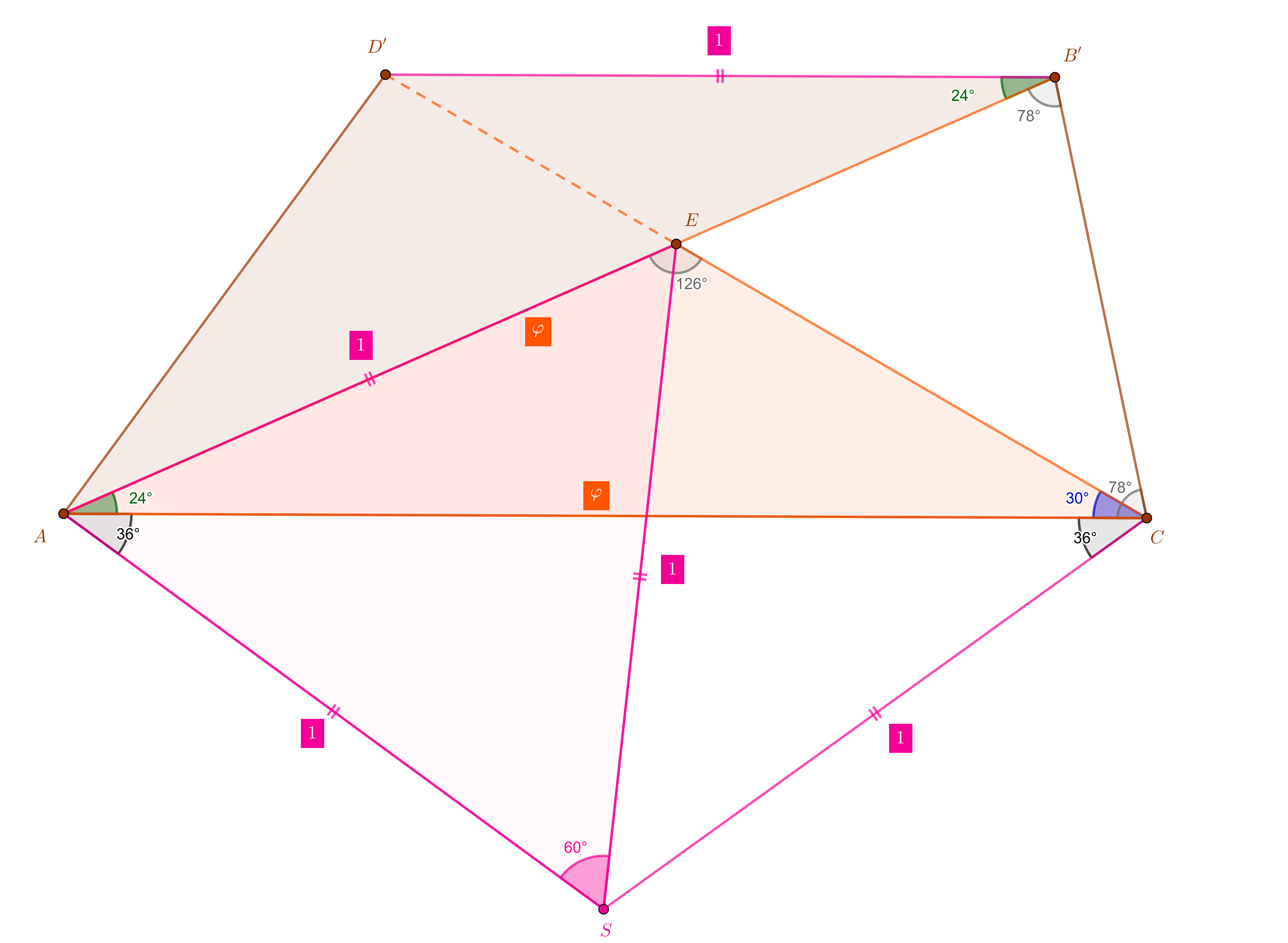
Solution using an explicit geometric construction: We are starting with $\Delta ACE$ with angles in $A,C,E$ of $24^\circ,30^\circ,126^\circ$. Construct the point $B'\in AE$ so that $\Delta AB'C$ is isosceles, $AB'=AC$. Its angles are $24^\circ,78^\circ,78^\circ$. Let $S$ be the circumcenter of $\Delta AEC$, so $\widehat{ASE}=2\cdot\widehat{ACE}=60^\circ$, making $\Delta AES$ equilateral, $SA=SE=SC=EA=\bbox[magenta]{\color{white}{\ 1\ }}$. Note that the angles in $\Delta ASC$ are $36^\circ,36^\circ,108^\circ$, so $A,S,C$ are consecutive vertices of a regular pentagon.
It is known that the proportion of the diagonal to the side in a regular pentagon is $$ \frac{AC}{AE}=\varphi=\frac 12(\sqrt 5+1)\ ,\qquad\varphi^2=\varphi+1\ . $$ We draw now a parallel from $B'$ to $AC$, and consider on it $D'$ as in the figure so that $B'D'=EA$.

(Are $C,E,D'$ on a line? Yes, this is our next task, a proof is needed.)

We show that the triangles $\Delta EAC$ and $\Delta EB'D'$ are similar. We have one angle of $24^\circ$ in each, so we need one more proportionality. We show $AC:B'D'=EA:EB'$, i.e. $\varphi:1=1:(\varphi-1)$, i.e. $\varphi^2-\varphi-1=0$, which is satisfied, the polynomial relation of the golden ratio.

This implies that the angles in $E$ in the similar triangles are both $126^\circ$, in particular, the segments $CE$ and $ED'$ are on the same line.

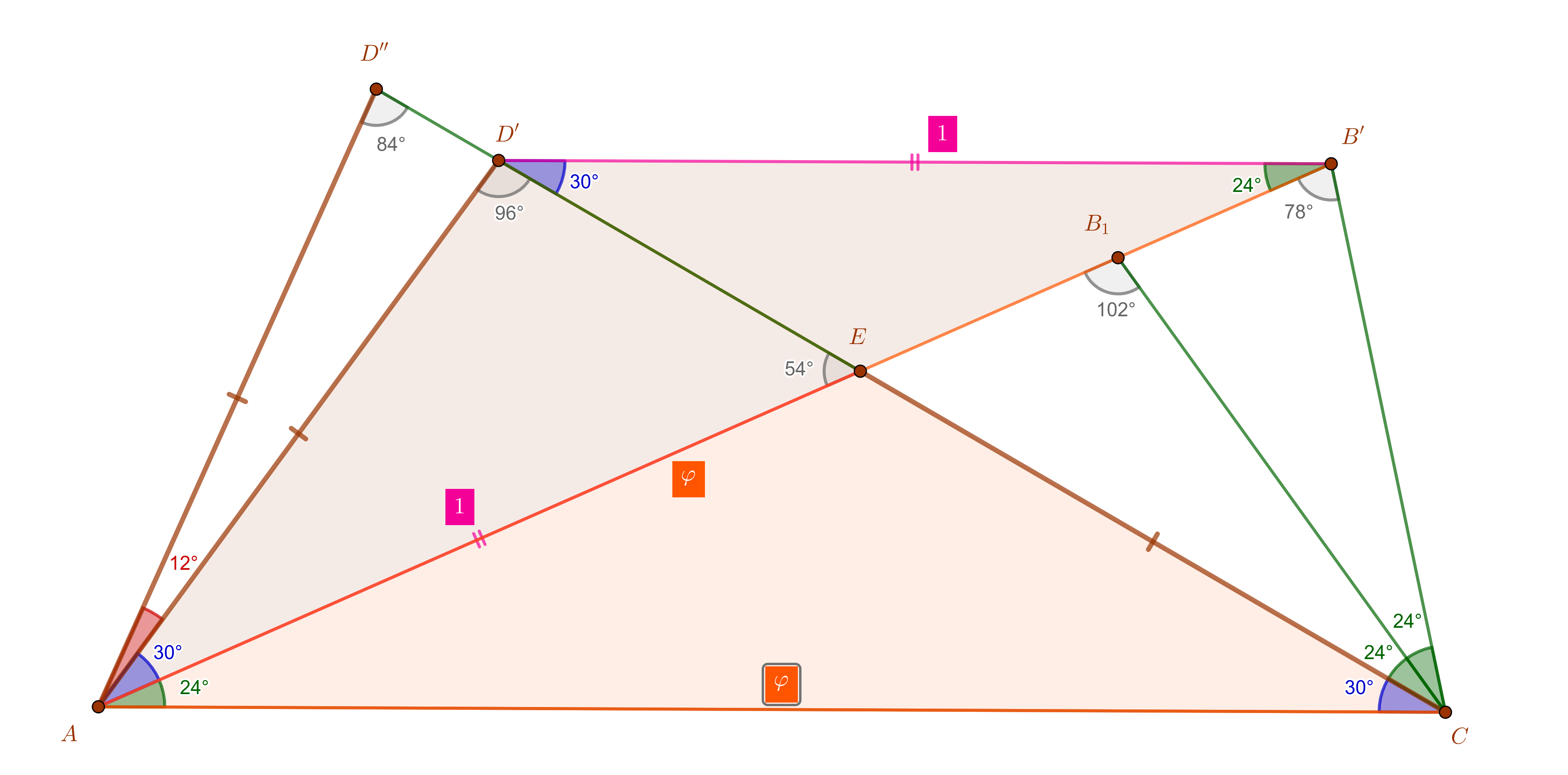
We compare now the triangles $\Delta EAC$ and $\Delta D'B'A$. We know an angle of $24^\circ$ in $A,B'$, and furthermore $EA=D'B'=1$, $AC=B'A$. So these triangles are congruent. We take this new information and construct the second point $D''$ on the ray $[CED'$ beyond $D'$ with $AD'=AD''$, i.e. $\Delta AD'D''$ isosceles in $A$ with angles $12^\circ,84^\circ,84^\circ$. Similarly there is $B_1\in AE$ with $\Delta CB'B_1$ isosceles in $C$ and angles $24^\circ,78^\circ,78^\circ$. We have by construction the following situation at this intermediate point:

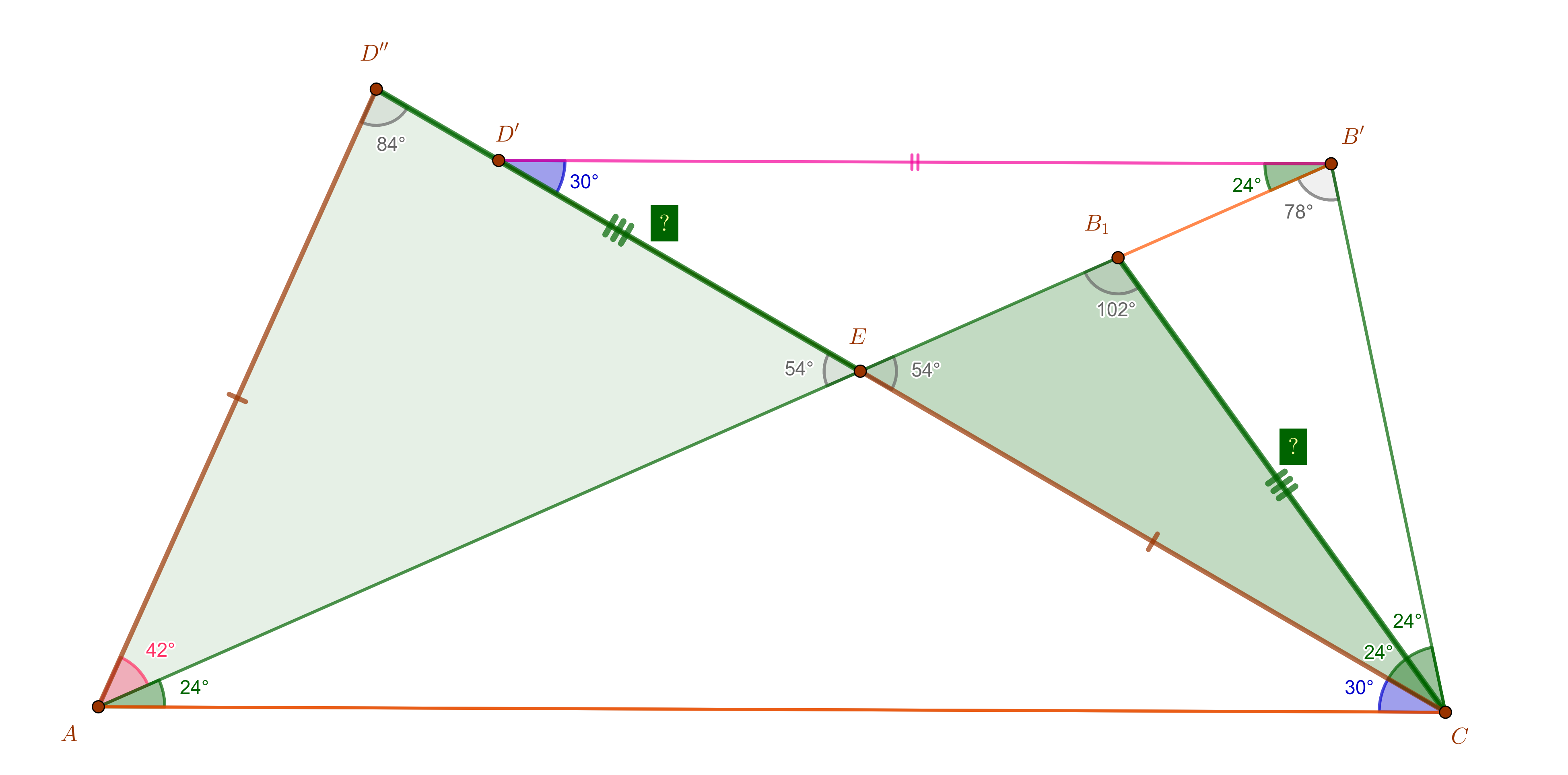
and by construction the equality (congruence) of the brown segments is insured, $CE=AD'=AD''$. We need only to prove the equality of the green segments $ED''$ and one of (known to be equal) $CB_1$, marked with thick green paint and with a question mark each in the following picture, which extracts from the above one the relevant pieces:

The two triangles are "divorced" from each other, so do the brown equal segments in them, too. Instead of searching for a construction in this wide spread constellation of points, we can bring the brown triangles together, and focus on the new placements of the green $?$-segments. So it is enough to show the following:

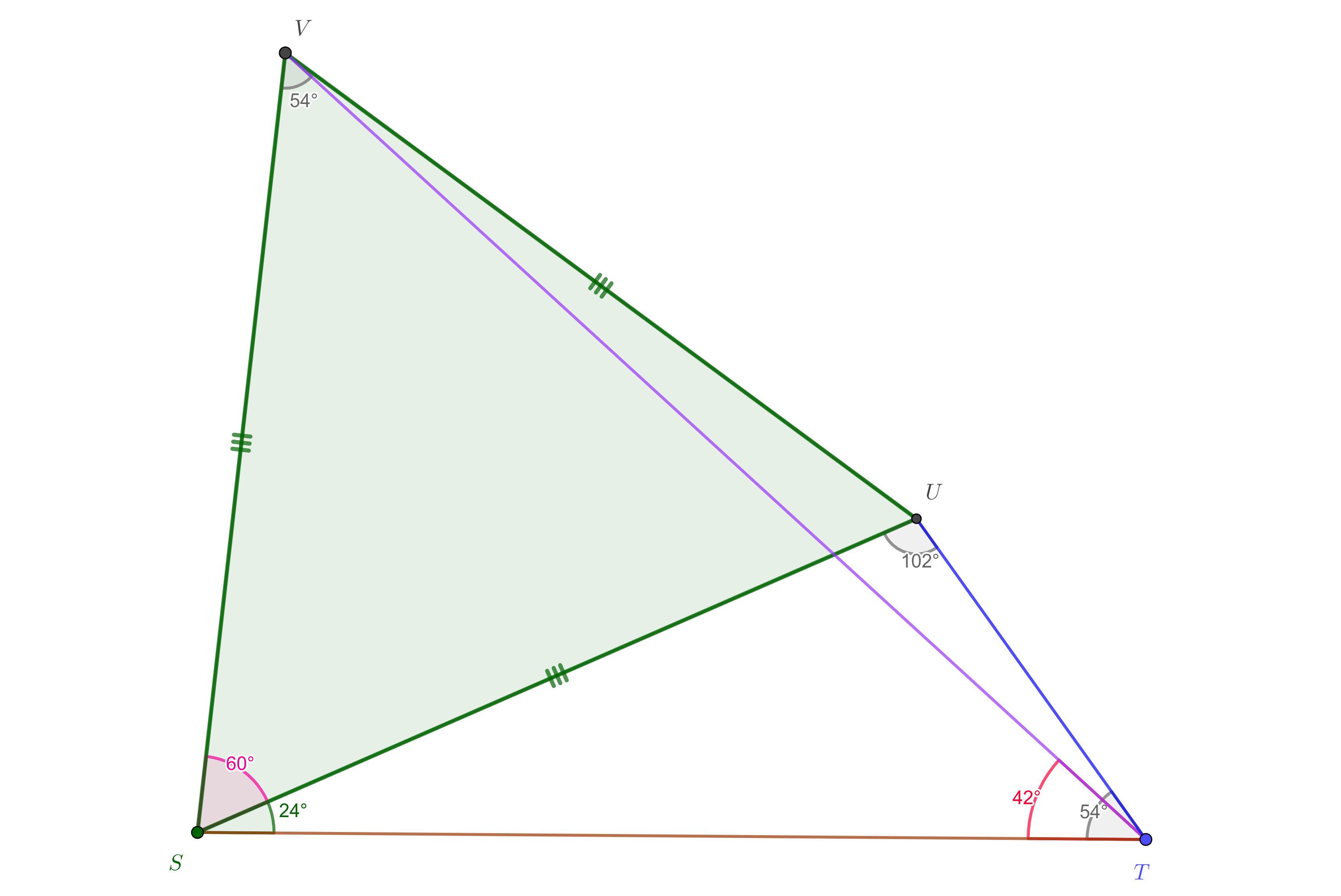
Lemma: Fix a segment $ST$. Construct in the same half-plane two triangles $\Delta STU$ with angles in $S,T,U$ of respectively $24^\circ,54^\circ,102^\circ$, and $\Delta STV$ with angles in $S,T,V$ of respectively $84^\circ,42^\circ,54^\circ$. Then $\Delta SUV$ is equilateral.

---

Proof of the lemma: It is natural to construct the following constellation of points by starting with the equilateral triangle. (Indirect proof. We construct points, and finally the wanted constellation of points from the lemma is obtained by the richer properties of the introduced objects.)

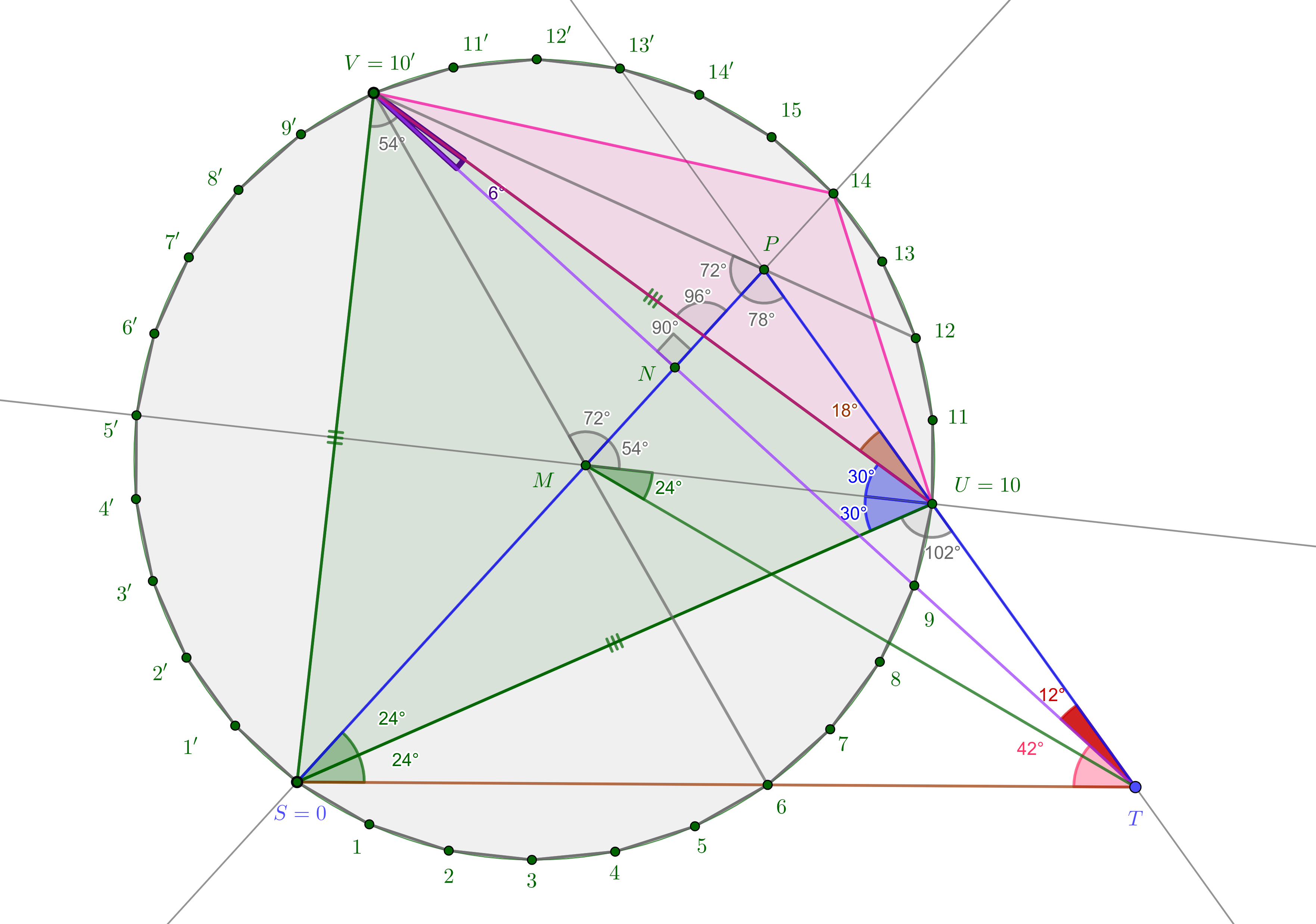
The involved angles are multiples of $6^\circ$, and because of this it is natural to realize the hole construction by starting from a $30$-gon. We do so and denote its vertices by numbers $0,1,2,\dots$ and in order to use smaller numbers, let a prime denote the reflection w.r.t. the diameter from $0$ to $15$. So the set of vertices is cyclicly ordered as $0,1,2,3,\dots, 13,14,15,14',13',\dots,3',2',1'$. Let us place the points $S,U,V$ from the lemma in $0,10,10'$. Angles formed by two chords of the $30$-gon are easily computed. An inscribed angle that "looks to" a chord or to an arc between two consecutive marked nodes / vertices has $6^\circ$. For the double arc we have the double measure, $12^\circ$, triple arc $18^\circ$, and so on...

Consider now the following figure, and we introduce one by one the yet unknown points.

Consider the pink triangle with vertices $U=10$, $14$, $V=10'$. Let $P$ be its incenter, the intersection of the angle bisectors, which are the three lines $U,13'$, and $V,12$, and $14,S$. The angle $\widehat {SPU}$ has the measure $(13+3)\cdot 6^\circ$. (There are $13$ "inscribed pieces" on the arc $\overset{\large\frown}{SU}$ and $3$ further ones on the arc $\overset{\large\frown}{14,13'}$.)

Let $M$ be the intersection of the diameter $U5'$, which is also the angle bisector from $U$ in $\Delta SUV$, and the two chords which are symmetric with respect to this diameter, $V,6$ and $S,14$. Then the angles in $M,P$ in $\Delta VMP$ are $\hat M=(6+6)\cdot 6^\circ=72^\circ$ and $\hat P=(10+2)\cdot 6^\circ=72^\circ$. So this triangle is isosceles in $V$, $VP=VM$. Let $N$ be the mid point of $MP$. Then $VN\perp MP$, i.e. the line $VN$ is the perpendicular bisector of $MP$. (We know the angle $\widehat {MVN}=90^\circ-72^\circ=18^\circ$, so $VN$ goes through $9$.)

Let $T$ be the intersection of $S,6$ and $13',P,U$. Then we have angles with the same measure, $\widehat{PUM}=8\cdot 6^\circ= \widehat{MST}$, so $MSTU$ cyclic. This shows $\widehat{UMT}=\widehat{UST}=24^\circ$, so $\Delta TMP$ has equal angles of $78^\circ$ in $M,P$. It is isosceles, so $TN$ is also the perpendicular bisector of $MP$, as $VN$. The points $V,N,9,T$ are thus collinear.

Consider the triangle $\Delta STV$. Its angles in $V,S$ are $\hat V=\widehat {SV9}=\widehat {0V9}=9\cdot 6^\circ=54^\circ$, and $\hat S=\widehat {6SV}=14\cdot 6^\circ=84^\circ$.

Consider the triangle $\Delta STU$. Its angles in $S,T$ are $\hat S=\widehat {US6}=24^\circ$, and $\hat T=\widehat {UMP}=54^\circ$.

So we realized a constellation of two triangles as in the lemma.

$\square$

---

Putting all together we have a complete synthetic proof of the claimed proposition.

As a final note, i would like to mention that a direct proof using a regular $30$-gon may be tried from the start, without breaking the story into pieces and solving two smaller problems. It depends on showing a concurrence of chords in this regular polygon. However, i could not find a simple argument for the "direct map" of the given constellation, as the used argument involving the concurrence of the angle bisectors of $\Delta U\; V\; 14$ above.