I am reading the Gortz's Wedhorn, Algebraic Geometry, p.414~p.415 ( dealing with construction of blow-up and its universal property ) and stuck at some (final) statement. Although the universal propdery of blow-up is proved in the Stack's project, Lemma 31.32.5 ( https://stacks.math.columbia.edu/tag/0806 ), I think that its proof is somewhat difficult to understand. I've searched several sites to find explanation of such final stucked statement, but there doesn't seem to be a satisfactory answer yet.
First note next definitions and lemma of stacks project and Gortz / Wedhorn.
Definition 31.13.1. An effective Cartier divisor on $S$ is a closed subscheme $D \subset S$ whose ideal sheaf $\mathcal{I}_D \subset \mathcal{O}_S$ is an invertible $\mathcal{O}_S$-module.
Lemma 31.13.2. ( https://stacks.math.columbia.edu/tag/01WS ) Let $S$ be a scheme. Let $D\subseteq S$ be a closed subscheme. The following are equivalent :
- (1) The subscheme $D$ is an effective Cartier divisor on $S$.
- (2) For every $x\in D$ there exists an affine open neighborhood $\operatorname{Spec}A=U\subset S$ of $x$ such that $U\cap D = \operatorname{Spec}(A/(f)) = V(f)$ with $f\in A$ nonzerodivisor .
Definition 13.90. ( Gortz, Wedhorn ) Let $X$ be a scheme and let $Z$ be a closed subscheme. A blow up of $X$ along $Z$ is a scheme $\tilde{X}$ and a morphism $\pi : \tilde{X} \to X$ such that $\pi^{-1}(Z)$ is an effective Cartier divisor and which is universal with respect to this property: If $\pi' : \tilde{X}'\to X$ is any morphism such that $\pi'^{-1}(Z)$ is an effective cartier divisor, then there is a unique morphism $g: \tilde{X}' \to \tilde{X}$ such that $\pi'=\pi \circ g$.
Second let me present Gortz / Wedhorn's argument for constructing blow up ( their book p.414 ~ p.415 ) :
In second paragraph in the argument, I convinced the possibility of reduction to $X=\operatorname{Spec}A$ affine. We accept this statement.
Q. Why the underlined statement is true? I understand that $\pi : \tilde{X} \to X$ is in the category ; i.e., $\pi^{-1}(Z)$ is effective Cartier divisor ( C.f. https://stacks.math.columbia.edu/tag/02OS ) . And I don't understand the remaining part.
$\divideontimes$ My first attempt to understand : Perhaps, next is possible? :
For each $f\in I$, there exists an $A$-algebra $\varphi_f : A \to C_f$ such that
-
- $\operatorname{Spec}(C_f)$ ( $ f \in I$) forms an open cover of $Y$.
-
- $\operatorname{Spec}(\varphi_f) : \operatorname{Spec} C_f \to \operatorname{Spec} A =X$ glues to $g : Y \to X$.
-
- $\varphi_f$ satisfies that 3-1) $\varphi_f ( f) \in C_f$ is regular ( nonzero divisor ) and 3-2 ) $\varphi_f(f)$ generates $\varphi_f(I)C_f$
?
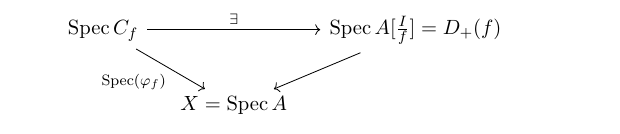
If this is ture, then as in the arguement there exists a unique $A$-algebra homomorphism $A[\frac{I}{f}] \to C_f$. We have commutative diagram :
By taking $\operatorname{Spec}$, we have
Then, by gluing, we have a (unique?) morphism $h: Y \to \tilde{X}=\bigcup_{f\in I}D_{+}(f)$ such that $g = \pi \circ h$. And can we really construct such $A$-algebras $\varphi_f : A \to C_f$ ? Can we try to use the Lemma 31.13.2 above? I don't understand these stuff at all. Can anyone help?
EDIT ( Second attempt to understand ) : I found associated reference : https://achinger.impan.pl/rigid/blowups.pdf . In the reference, page 4 above, the author noted that ( considering slight change in symbol ) " Since the affine opens $\operatorname{Spec}A[I/f]$ cover $\tilde{X}$, it suffices to show :
Every map $g : Y\to X$ such that the ideal of $g^{-1}(Z) \subseteq Y$ is invertible and generated by $f$ factors uniquely through $\operatorname{Spec}A[I/f]$."
Why this statement is sufficient? What the sentence 'generated by $f$' exactly means? And after establishment of this sufficiency, the author argues that "We can assume that $Y=\operatorname{Spec}C$ is affine. Then the assertion follows from the commutative algebra sublemma below. ( as argued in the final paragraph of the above image )
Sublemma. Let $A$ be a ring, $I \subseteq A$ an ideal, $f\in I$ an element. Then every homomorphism $\varphi : A \to C$ such that $\varphi(I)C= \varphi(f) C$ and $\varphi(f)$ is a nonzero-divisor in $C$ factors uniquely through the affine blowup algebra $A[I/f]$.
To apply the sublemma for the case $Y=\operatorname{Spec}C$, first let $\varphi : A\to C$ be the induced ring homomorphism from the $g : Y \to X$. Then the above condition "the ideal of $g^{-1}(Z)= V(\varphi(I)C) \subseteq Y$ is invertible and generated by $f$" guarantees that $\varphi(I)C= \varphi(f)C$ and $\varphi(f)$ is a nonzero-divisor in $C$ ?
Can anyone explain these argument more friendly?