First, the coordinates given have to corrected with respect to the center. As mentioned in question, the size of the image is $3024 \times 4032$ pixels. Therefore, the coordinates of the center are $( \dfrac{3024}{2}, \dfrac{4032}{2}) = (1512, 2016) $. With this, the corrected coordinates becomes
$P_1 = (986, -1153)$
$P_2 = (-991, -1183)$
$P_3 = (-831, 1254) $
$P_4 = (778, 1240) $
And
$ P_2' = (697, 1007) $
$P_3' = (1122, -892)$
$P_4' = (-1241, -854)$
$Q' = (-144, -80) $
Next, we have to find the focal length $z_0$ of the camera. This is only possible if the four given points are the four corners of a rectangle, as is the case here. So taking four rays of the form
$ R_i = t_i \begin{bmatrix} P_i \\ z_0 \end{bmatrix} $
If the $R_i$'s are vertices of a rectangle then two conditions must be satisfied:
$R_2 - R_1 = R_3 - R_4 $
$ (R_2 - R_1) \cdot (R_3 - R_2) = 0 $
The first of these equations gives a linear system of three equations in the four unknown $t_i$'s. Its solution is
$ (t_1, t_2, t_3, t_4) = \lambda \mathbf{v} $
where $\mathbf{v} \in \mathbb{R}^4 $ and is now known.
The second equation leads to a quadratic equation in $z_0$, and gives
$ z_0 = - \sqrt{ \dfrac{ (v_2 P_2 - v_1 P_1) \cdot ( v_3 P_3 - v_2 P_2) }{ (v_3 - v_2)(v_2 - v_1) }} $
We can take $\lambda = 1$, and compute the $R_i$'s.
From which we can compute the ratio $r = \dfrac{\| R_1 R_2 \|}{ \|R_2 R_3 \|} $
This ratio comes to $r \approx \dfrac{1}{\sqrt{2}} $.
Moving on to the second image, we only have three vertices known. So we'll write
$ R_i' = t_i' Q_i' , i = 2, 3, 4 $
We can take $t_2' = K $ where $K \gt 0$ is a chosen constant. This leaves two unknowns, $t_3' $ and $t_4'$ to be determined. To determine them we impose the following two conditions
$(R_2' - R_3') \cdot (R_4' - R_3') = 0 $
$\| R_4' - R_3'\|^2 = r^2 \| R_2' - R_3' \|^2 $
Solving this quadratic system leads to the values of $t_3'$ and $t_4'$. There can be more than one solution. In this case we have to choose the right one based on the direction of the normal vector to the plane defined by $R_2', R_3'$ and $R_4'$.
Having determined the correct values of $t_3'$ and $t_4'$ we now have $R_2', R_3', R_4'$.
We can now find the point $R_{Q'}$ whose corresponding image is point $Q'$ in the second image, by intersecting the ray from $Q'$ with the plane defined by $R_2', R_3', R_4'$.
The following step is to decompose the vector $R_{Q'} - R_3' $ into two (perpendicular) components along the two vectors $(R_2' - R_3') $ and $(R_4' - R_3')$, which is a trivial task.
So now we have
$ R_{Q'} = R_3' + \alpha (R_2' - R_3') + \beta (R_4' - R_3')$
Now we go back to the first image in which we know $R_2, R_3, R_4$ and write
$ R_Q = R_3 + \alpha (R_2 - R_3) + \beta (R_4 - R_3) $
Finally we have to intersect the ray from the origin to $R_Q$ with the plane $z = z_0$, again a trivial task.
Once we do that, we have the $2D$ vector $Q$.
Taking the center of view into consideration and adjusting the coordinates $Q$, we obtain the position coordinates in the image.
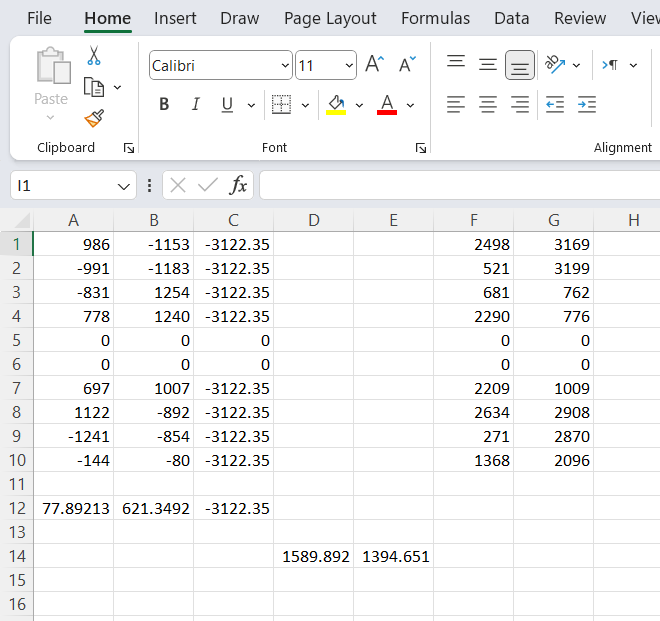
After running the above procedure on the given data, I obtained
$Q = (77.892, 621.349) $
Taking into account the coordinates of the center of view ( which are (1512, 2016) ), we get the coordinates for $Q$ relative to the top left corner of the image as
$ ( 1590, 1395 )$
which is very close to the values estimated by the OP. His estimate for the coordinates of $Q$ were $(1581, 1405)$.
Below is the implementation of the above steps, written in Excel VBA script. The source code for the functions "solve_rd_system" and "intersect_three_quadrics" is included in this Excel file as a macro (VBA script). Click on the link, to open the online file, then click on "Editing" and choose "Open in Desktop App". This will open the file in your desktop Excel program. Click "View" then select "Macros".
Public Sub calculate_position_of_q()
Dim pts(50, 2) As Double
Dim spoints(10, 3), points3d(10, 3) As Double
Dim xpts(10, 3) As Double
Dim q(4, 4, 3), qc(4, 4, 3), ipoints(8, 3) As Double
Dim ipoint As Integer
Dim points2_3d(4, 3) As Double
Dim a1, a2 As Double
Dim teez(3) As Double
Dim s1(3), s2(3), s3(3) As Double
Dim sol(3) As Double
Dim recpoints(6, 2) As Double
Dim sourcepoints(5, 3) As Double
Dim xp As Double, zp As Double
Dim r As Double
Dim center(3) As Double
Dim irp, isp As Integer
Dim pts0(10, 2) As Double
Dim x0(4), x1(4), xx(4, 4) As Double, mt As Integer, ierr As Integer
Dim ma(5, 5), bvec(5) As Double
Dim image1(5, 3) As Double
cx = 3024 / 2
cy = 4032 / 2
'-----------------Preprocessing: identify z0
For icorner = 1 To 4
xpts(icorner, 1) = ActiveSheet.Cells(icorner, 6) - cx
xpts(icorner, 2) = -(ActiveSheet.Cells(icorner, 7) - cy)
Next icorner
'
' t2 P2 - t1 P1 = t3 P3 - t4 P4
'
For i = 1 To 2
ma(i, 1) = -xpts(1, i)
ma(i, 2) = xpts(2, i)
ma(i, 3) = -xpts(3, i)
ma(i, 4) = xpts(4, i)
Next i
ma(3, 1) = -1
ma(3, 2) = 1
ma(3, 3) = -1
ma(3, 4) = 1
For i = 1 To 3
bvec(i) = 0
Next i
Call solve_rd_system(ma, bvec, 3, 4, mt, x0, xx, 0.00000001, ierr)
If mt <> 1 Then
MsgBox ("mt is not equal to 1. Cannot continue")
Exit Sub
End If
For i = 1 To 4
x1(i) = xx(i, 1)
Next i
' equation for z0
't^2 ( v1 P1 - v2 P2 ) . ( v3 P3 - v2 P2 ) = 0
'this will be a quadratic equation as follows
'(v1 - v2)(v3 - v2) z0^2 + K = 0
'this will give z0 (take the negative z0)
For i = 1 To 2
u1(i) = x1(1) * xpts(1, i) - x1(2) * xpts(2, i)
u2(i) = x1(3) * xpts(3, i) - x1(2) * xpts(2, i)
Next i
z0 = -Sqr(-dotn(u1, u2, 2) / ((x1(1) - x1(2)) * (x1(3) - x1(2))))
MsgBox ("z0 = " + Str(z0))
For ipoint = 1 To 4
xpts(ipoint, 3) = z0
Next ipoint
' compute the coordinates of the four corners in 3D
For icorner = 1 To 4
For j = 1 To 3
points3d(icorner, j) = x1(icorner) * xpts(icorner, j)
Next j
Next icorner
' find the ratio of the sides of the rectangle
For i = 1 To 3
u1(i) = points3d(1, i) - points3d(2, i)
u2(i) = points3d(3, i) - points3d(2, i)
Next i
r = norm(u1, 3) / norm(u2, 3)
' determine sense of points
For i = 1 To 2
u1(i) = xpts(2, i) - xpts(1, i)
u2(i) = xpts(3, i) - xpts(2, i)
Next i
u1(3) = 0
u2(3) = 0
Call cross(u1, u2, u3)
isense = Sgn(u3(3))
' now we're momentarily done with the first image. We'll move to the second image
For isp = 2 To 5
xpts(isp + 5, 1) = ActiveSheet.Cells(isp + 5, 6) - cx
xpts(isp + 5, 2) = -(ActiveSheet.Cells(isp + 5, 7) - cy)
xpts(isp + 5, 3) = z0
Next isp
For i = 1 To 2
s1(i) = xpts(7, i)
s2(i) = xpts(8, i)
s3(i) = xpts(9, i)
Next i
s1(3) = z0
s2(3) = z0
s3(3) = z0
For k = 1 To 3
For i = 1 To 4
For j = 1 To 4
q(i, j, k) = 0
Next j
Next i
Next k
q(1, 4, 1) = 0.5
q(4, 1, 1) = 0.5
q(4, 4, 1) = -15
q(1, 2, 2) = 0.5 * dot(s1, s2)
q(1, 3, 2) = -0.5 * dot(s1, s3)
q(2, 2, 2) = -(dot(s2, s2))
q(2, 3, 2) = 0.5 * dot(s2, s3)
q(1, 1, 3) = -(r ^ 2) * dot(s1, s1)
q(2, 2, 3) = (1 - r ^ 2) * dot(s2, s2)
q(3, 3, 3) = dot(s3, s3)
q(1, 2, 3) = (r ^ 2) * dot(s1, s2)
q(2, 3, 3) = -(dot(s2, s3))
For k = 1 To 3
For i = 2 To 4
For j = 1 To i - 1
q(i, j, k) = q(j, i, k)
Next j
Next i
Next k
Call intersect_three_quadrics(q, qc, ipoints)
MsgBox ("no. of possibilities =" + Str(ipoints(0, 0)))
lfirst = 1
' we need all the t's to be positive
icount = 0
lfound = 0
For isol = 1 To ipoints(0, 0)
If ipoints(isol, 1) > 0 And ipoints(isol, 2) > 0 And ipoints(isol, 3) > 0 Then
icount = icount + 1
For i = 1 To 3
sol(i) = ipoints(isol, i)
Next i
Else
MsgBox ("solution rejected")
GoTo lnext_isol1
End If
For ipoint = 1 To 3
For i = 1 To 3
points3d(ipoint + 6, i) = sol(ipoint) * xpts(ipoint + 6, i)
Next i
Next ipoint
For i = 1 To 3
u0(i) = points3d(8, i)
u1(i) = points3d(7, i) - points3d(8, i)
u2(i) = points3d(9, i) - points3d(8, i)
u4(i) = xpts(10, i)
Next i
Call cross(u1, u2, u3)
If Sgn(u3(2)) = isense Then
MsgBox ("Solution no. " + Str(isol) + " rejected")
GoTo lnext_isol1
End If
lfound = 1
' equation of plane where q' lies is u3^T ( t u4 - u0) = 0
t1 = dot(u0, u3) / dot(u3, u4)
For i = 1 To 3
points3d(10, i) = t1 * u4(i)
u5(i) = t1 * u4(i)
Next i
' decompose points3d i.e. u5 in terms of u0, u1, u2
' u0 + t u1 + s u2 = u5
' t u1 + s u2 = u5 - u0 = u6
For i = 1 To 3
u6(i) = u5(i) - u0(i)
Next i
a1 = dot(u6, u1) / dot(u1, u1)
a2 = dot(u6, u2) / dot(u2, u2)
MsgBox ("a1 =" + Str(a1) + ".... a2 = " + Str(a2))
Exit For
lnext_isol1:
Next isol
If lfound = 0 Then
MsgBox ("No. valid solutions found. Exiting")
Exit Sub
End If
'-------------------------------------------------
For i = 1 To 3
u0(i) = points3d(3, i)
u1(i) = points3d(2, i) - points3d(3, i)
u2(i) = points3d(4, i) - points3d(3, i)
Next i
For i = 1 To 3
u3(i) = u0(i) + a1 * u1(i) + a2 * u2(i)
Next i
' projection of u3 in 2D is found by intersecting the ray (t u3) with k^T (r - z0 (k)) = 0
t2 = z0 / u3(3)
For i = 1 To 3
u4(i) = t2 * u3(i)
Next i
For i = 1 To 3
ActiveSheet.Cells(12, i) = u4(i)
Next i
u1(1) = u4(1) + cx
u1(2) = cy - u4(2)
For i = 1 To 2
ActiveSheet.Cells(14, i + 3) = u1(i)
Next i
For ipoint = 1 To 10
For j = 1 To 3
ActiveSheet.Cells(ipoint, j) = xpts(ipoint, j)
Next j
Next ipoint
End Sub
This is an image of the Excel worksheet that produced these results.
The input data is in columns $F$ and $G$. The rest is output.