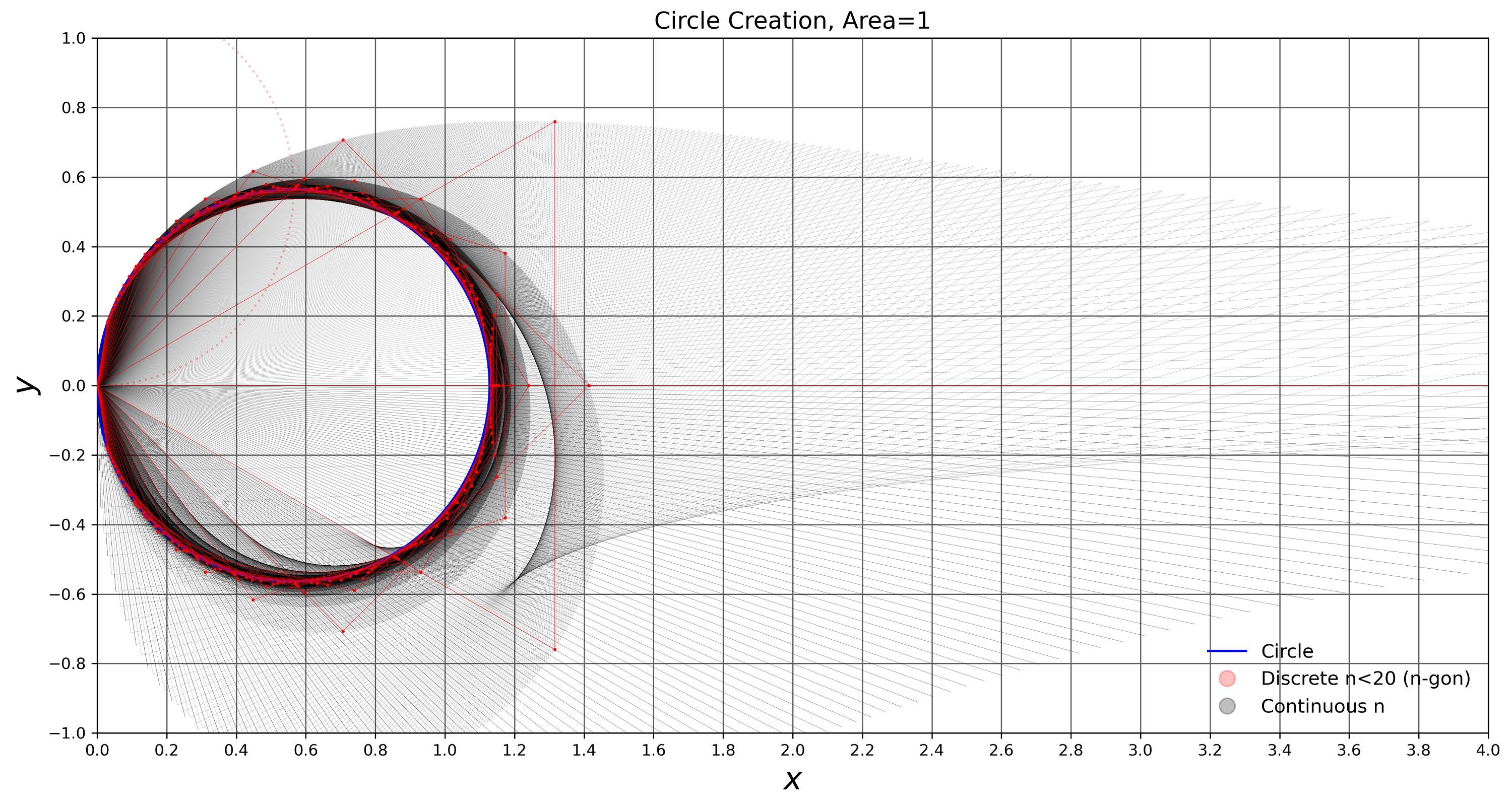
To gain more intuitive nature about the irrational and transcendental behavior of $\pi$ circles were constructed with $n$-gons circumference $C=1$ see [SE].
This method however describes how a circle (I think) can be created from $n$-gons with area: $A=1$.
While I am no math expert I would like to know if the method is valid. I cannot find a similar method on internet for reference.
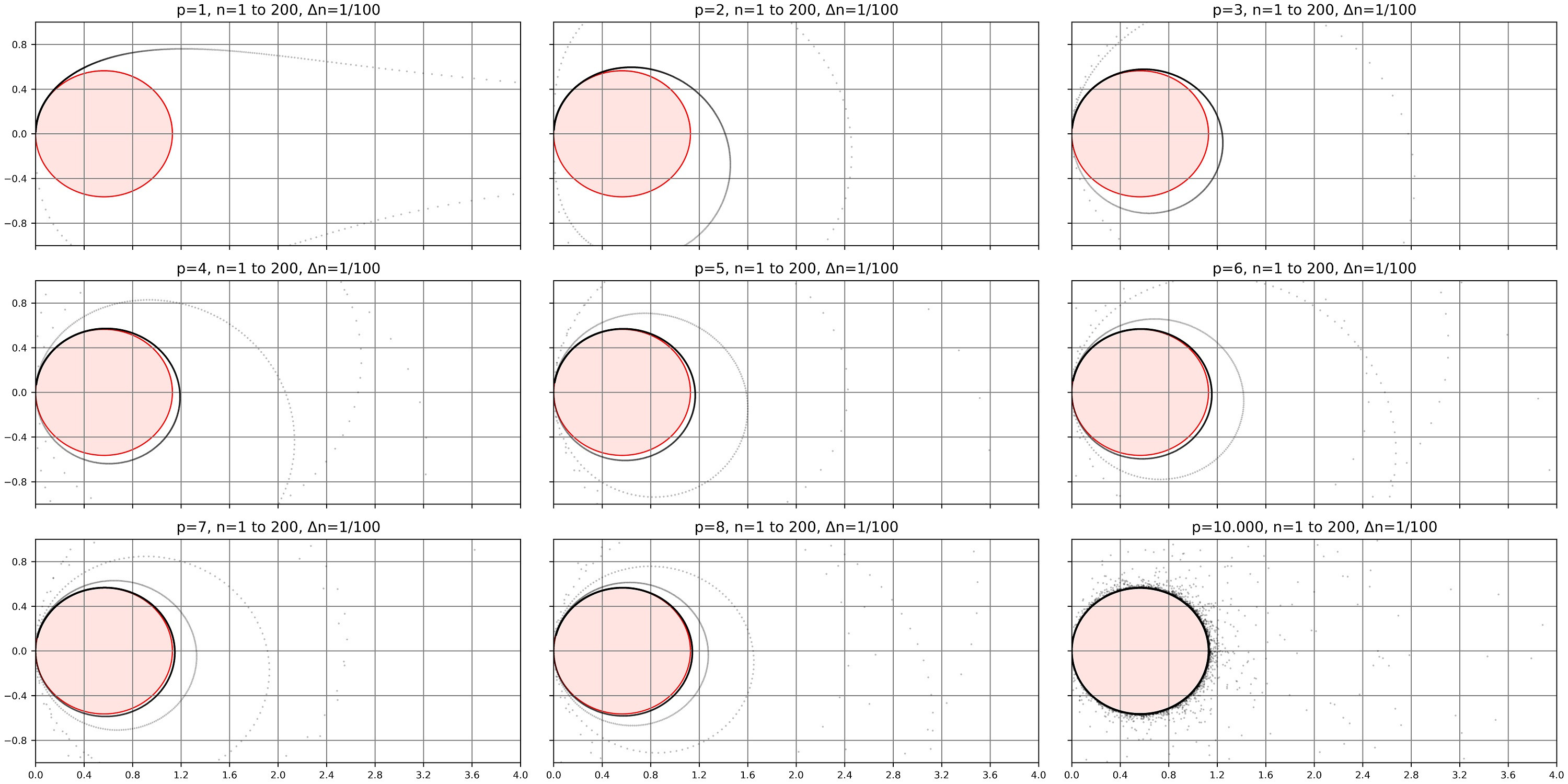
Polygons with $n$ sides ($n$-gons) can be defined as function of the side length $s$ and the angle between $3$ neighbor edge points. The $n$-gons are defined such that one edge point is in the origin.
$$x=s \cdot \sum_{k=0}^{p} \cos \left(\frac{2k+1}{n} \pi \right)$$ $$y=s \cdot \sum_{k=0}^{p} \sin \left(\frac{2k+1}{n} \pi \right)$$
Normally summing $p=n$ elements completing one pass $360^{\circ}$. The area of all $n$-gons is set to $A=1$. The side length $s$ can be determined with $n$-gon area formula [Wiki]:
$$A=\frac{ns^{2}}{4 \cdot \tan \left( \frac{\pi}{n} \right)}=1$$ $$s=2 \cdot \sqrt{ \frac{ \tan \left( \frac{\pi}{n} \right)}{n} }$$
Resulting in the following $n$-gons:
$$x=2 \cdot \sqrt{ \frac{ \tan \left( \frac{\pi}{n} \right)}{n} } \cdot \sum_{k=0}^{p} \cos \left(\frac{2k+1}{n} \pi \right)$$ $$y=2 \cdot \sqrt{ \frac{ \tan \left( \frac{\pi}{n} \right)}{n} } \cdot \sum_{k=0}^{p} \sin \left(\frac{2k+1}{n} \pi \right)$$
Empirical (see graphs) it is found that $n$ and $k$ could be continuous numbers, though not sure if that is valid hence the question. By integration a circle formula is found:
$$x=2 \cdot \sqrt{ \frac{ \tan \left( \frac{\pi}{n} \right)}{n} } \cdot \int \cos \left(\frac{2k+1}{n} \pi \right)dk=\frac{n}{\pi}\cdot \sqrt{ \frac{ \tan \left( \frac{\pi}{n} \right)}{n} } \cdot \sin \left(\frac{2k+1}{n} \pi \right)$$ $$y=2 \cdot \sqrt{ \frac{ \tan \left( \frac{\pi}{n} \right)}{n} } \cdot \int \sin \left(\frac{2k+1}{n} \pi \right)dk=-\frac{n}{\pi}\cdot \sqrt{ \frac{ \tan \left( \frac{\pi}{n} \right)}{n} } \cdot \cos \left(\frac{2k+1}{n} \pi \right)$$
This parametrized function gives us a circle if the radius $R$ of the circle exists [Wolfram]:
$$R_{\infty}= \frac{1}{\pi}\cdot \lim_{n \rightarrow\infty} \sqrt{ n \cdot \tan \left( \frac{\pi}{n} \right) } = \frac{1}{\sqrt{\pi}}$$
The radius seems to exist in infinity. We set the area of the $n$-gons $A=1$ the area of the final circle becomes:
$$A=\pi R^{2}=\pi \cdot \left( \frac{1}{\sqrt{\pi}} \right)^{2}=\frac{\pi}{\pi}=1$$
Here the final circle has the same area as the $n$-gons.
Question [Edit].
While I am no math expert I would like to know if the method is valid and where it needs correction. I cannot find a similar method on internet for reference.
I am having difficulties swapping discrete $n$ and $k$ for continuity. More information about continuity in this context is welcome.
With circle creation $n$-gon area $A=1$ the found radius $R_{\infty}=1/\sqrt{\pi}$ is a limit value. Circle creation $n$-gon circumference $C=1$ [SE], the radius $R=1/{2 \pi}$ is better defined (no limit value). Why is a circle with $C=1$ better defined as $A=1$?
Could a similar method also be scaled up to $3d$ with polyhedron's. (Platonic solid's)? First thought it is not possible while the numbers of edges grow irregular. Ideas are welcome.
Graph 1: $n$-gons discrete and continuous.
(x and y swapped so graph is landscape)