Critical points of Torus height function

Question

I'm reading Tu's intro to manifolds. He defines a critical point of a smooth map $F:N\to M$ to be a point where the differential $F_{*,p}:T_pN\to T_{F(p)}M$ fails to be surjective. He then gives illustration of the $2$ torus embedded in three space, standing vertically with a height function $f(x,y,z)=z$ given. So in this example, the differential at a critical point would have to be the zero map, as it would otherwise be surjective onto $\mathbb{R}$.

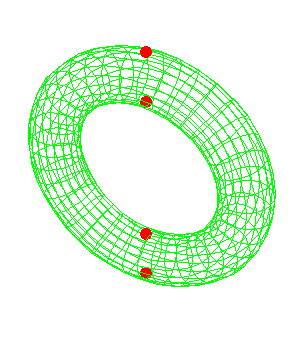
So I should be able to see just from the picture that there are four critical points as shown. But I don't know why. Is it because the tangent plane at each of these points is flat (i.e. every point in the tangent plane is at the same height)? If so, why would that make the differential not onto? After this example, he explains that $p$ is critical if $\frac{\partial f(p)}{\partial x^1}=,...,=\frac{\partial f(p)}{\partial x^n}=0$ for some coordinate neighboorhood of $p$, but since the example comes before this theorem, I should be able to understand the example without it.

Answer 1

Your map $f: \mathbb{T}^2 \to \mathbb{R}$ is the restriction of the projection function $\pi_z : \mathbb{R}^3 \to \mathbb{R}$. Since this is a linear map, identifying $\mathbb{R}^3$ with its tangent space at each point and likewise for $\mathbb{R}$, the differential of $\pi_z$ is just $\pi_z$. In particular, its kernel is the $xy$ plane.

This helps us to figure out the differential of $f$. After all, $f$ is the composition of the inclusion map $\mathbb{T}^2 \hookrightarrow \mathbb{R}^3$ and $\pi_z$, so $df_p$ is the composition of $T_p \mathbb{T}^2 \hookrightarrow \mathbb{R}^3$ and $\pi_z$. This is the zero map exactly when the image of $T_p \mathbb{T}^2$ in $\mathbb{R}^3$ is contained in the $xy$ plane. This is the condition you should be looking for; the points you've identified are clearly the only points at which the tangent plane is the $xy$ plane, hence they're the critical points.