Sistema di coordinate terrestri

Un sistema di coordinate terrestri è un insieme di parametri uniti a formare una terna di funzioni di punti sufficientemente regolari X_i(P) (i=1,2,3), grazie alla quale si identificano in maniera univoca gli oggetti sulla superficie terrestre. La posizione degli oggetti viene espressa mediante un sistema di coordinate riferite ad un opportuno sistema geodetico di riferimento (Datum). I sistemi di coordinate sono molti e tra loro equivalenti, è possibile passare da uno all’altro mediante l'utilizzo di opportune formule matematiche. Ogni sistema di coordinate può essere materializzato solo attraverso misurazioni che legano fisicamente gli elementi caratteristici del sistema di coordinate con i punti oggetto di rilievo.

Coordinate cartesiane

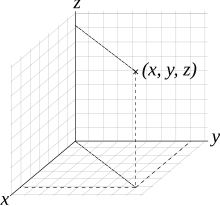
Le coordinate cartesiane permettono di individuare la posizione dei punti nello spazio attraverso quello che viene detto sistema di coordinate cartesiane. Tale sistema di riferimento viene stabilito mediante l'assunzione di tre assi fissati, detti assi cartesiani, indicati dalle lettere X, Y, e Z. Le caratteristiche dei tre assi consistono nell'essere ortogonali tra loro e nell'incontrarsi in un unico punto, definito origine degli assi e solitamente indicato con O. I tre assi identificano tre differenti piani all'interno dello spazio, i piani xy, xz e yz, che corrispondono in figura rispettivamente al piano orizzontale, al piano verticale a sinistra dell'asse Z (orientato) e al piano verticale a destra dell'asse Z. Ciascun punto è individuato attraverso la distanza che lo divide da ognuno dei tre assi, mediante l'utilizzo di tre coordinate (x,y,z), una per asse. Una caratteristica fondamentale del sistema di coordinate cartesiane è la possibilità di proiettare tutti i punti dello spazio ortogonalmente a determinati piani, a loro volta ortogonali tra loro, in modo da riuscire a rappresentare elementi e superfici tridimensionali su di un piano. Tali proiezioni prendono il nome di proiezioni ortogonali. Le proiezioni ortogonali, caratteristica unica all'interno dei sistemi di riferimento, rendono quello delle coordinate cartesiane un sistema puramente geometrico, regolare in tutto lo spazio e privo di singolarità.

Coordinate sferiche

Le coordinate sferiche (o polari) sono un sistema di coordinate che permette di esprimere la posizione di un punto nello spazio in alternativa alle coordinate cartesiane. Le coordinate sferiche vengono determinate tramite i tre parametri ( $\rho$ , $\theta$ , $\phi$ ). La relazione tra le coordinate sferiche e quelle cartesiane è dettata dalle seguenti equazioni:

x=\rho \sin \theta \ \cos \phi

y=\rho \sin \theta \ \sin \phi

z=\rho \cos \theta

Gli intervalli che definiscono i tre parametri sono $\left[0,+\infty \right)$ per $\rho$ , $\left[0,\pi \right)$ per $\theta$ , e $\left[0,2\pi \right)$ per $\phi$ .

Questo sistema di coordinate, chiamato sistema di coordinate sferiche, è simile al sistema della latitudine e longitudine utilizzato per la Terra in approssimazione sferica. In particolare considerando l'asse Z come l'asse di rotazione terrestre, la latitudine $\delta$ , complementare di theta, è determinata dalla relazione $\delta =90^{\circ }-\theta$ , e la longitudine est $l=\phi$ (se $\phi$ compreso fra 0° e 180°) ovvero la longitudine ovest $l=-\phi$ (se $\phi$ compreso fra -180° e 0°), se il semipiano $xz$ (con x>0) contiene il cerchio massimo passante per meridiano di Greenwich.

Coordinate ellissoidiche

Le coordinate ellissoidiche si basano sullo stesso principio delle coordinate sferiche ma usano un ellissoide invece che una sfera come superficie di riferimento che viene detto anche sferoide. Fissato un ellissoide di rotazione, un punto sull'equatore, considerando la normale all'ellissoide passante per il punto allora definisco le coordinate ellissoidiche del punto $P(\phi ,\lambda ,h)$ .

Coordinate intrinseche

Il sistema di coordinate intrinseche è completamente determinato dal campo gravitazionale terrestre, per questo è particolarmente indicato per descrivere le grandezze che dipendono direttamente dalla gravità. La terna (Φ_p,Λ_p,C_p) è costituita da tre funzioni di punti che garantiscono in maniera univoca la definizione della posizione dell'oggetto. I primi due termini sono quelli riferiti alla planimetria e vengono descritti tramite le coordinate astrogeodetiche (o naturali o intrinseche) o geografiche, il terzo è quello altimetrico. L'altimetria può essere definita con metodi differenti:

usare il valore del potenziale gravitazionale terrestre W_p

(diminuisce allontanandosi dalla superficie della Terra).

usare la quota geopotenziale C:

$C={\frac {W_{0}-W_{p}}{1000}}$

dove:

$W_{0}-W_{p}=\int _{o}^{p}g\,dn$ (detto numero geopotenziale)

per determinare W₀ si deve scegliere tra le infinite superfici equipotenziali una di riferimento G attraverso cui poi si determina il numero geopotenziale. Considerando il fattore 1000 come una costante dimensionale in [Gal], C espressa in [m].

quota ortometrica

$H=arco(P_{0}P)$

misurata lungo la verticale (direzione del filo a piombo) fino alla superficie del geoide.

Coordinate astrogeodetiche

Le coordinate astrogeodetiche vengono calcolate rispetto ad un sistema di riferimento fisso che assume come assi l'equatore celeste e l'asse di rotazione terrestre (inclinato di 23° 27' rispetto al piano dell'eclittica). Inizialmente si utilizzano come coordinate la declinazione (delta) e l'ascensione retta (alpha), le quali individuano univocamente le posizioni degli astri nella sfera celeste rispetto ad un punto d'origine fisso: primo punto d'Ariete, determinato dall'intersezione tra l'eclittica e l'equatore celeste (cerchio massimo). Tali coordinate risultano essere indipendenti dal moto di rotazione della Terra dato che sono fissate alla volta celeste. La conoscenza delle posizioni degli astri permette di individuare lo zenit, ovvero la verticale sulla sfera celeste. Considerando il movimento rotatorio della Terra, attorno all'asse di rotazione istantaneo, fisso rispetto alla sfera celeste, con velocità angolare istantanea (supposta costante) concludiamo che lo zenit di un punto gira in modo solidale alla Terra. Attraverso osservazioni alle stelle e misure di tempo è possibile definire le coordinate planimetriche intrinseche (ovvero dipendenti unicamente dalla gravità terrestre) del punto di osservazione attraverso gli angoli $\Lambda _{p},\Phi _{P}$ . Questi angoli vengono definiti a partire dalla verticale alla superficie del punto di osservazione $n_{p}$ ,il versore dell'asse di rotazione terrestre $e_{r}$ , e la perpendicolare nel punto di Greenwich $n_{gr}$ . Le formule che definiscono la latitudine e longitudine intrinseche sono:

$\sin \Phi _{p}=e_{r}\cdot n_{p}$
$\cos \Delta _{p}={\frac {e_{r}\land n_{gr}}{\cos \Phi _{gr}}}\cdot {\frac {e_{r}\land n_{p}}{\cos \Phi _{p}}}$

Nel calcolo delle coordinate astrogeodetiche vengono fatte determinate ipotesi che corrispondono a specifici coefficienti correttivi:

L'asse di rotazione istantanea terrestre viene preso fisso, non si considerano quindi i moti di precessione e nutazione (dovuto all'attrazione luni-solare) e le influenze dovute al moto di altri pianeti.
La velocità angolare, supposta costante, in realtà varia con oscillazioni dovute al momento angolare dell'atmosfera e degli oceani.
La materiaizzazione dell'asse d'istantanea rotazione non è costante, ma risente dell'oscillazione di Chandler Wobble, costituita da una componente giroscopica, dovuta all'interazione nucleo liquido e mantello elastico e altre interazioni dovute ai moti convettivi della Terra.
Il vettore $n$ di $\Lambda ,\Phi$ risulta variabile nel tempo in seguito all'azione diretta di attrazione luni-solare e all'effetto indiretto delle maree terrestri con periodi di circa 2 cicli al giorno. Variazioni che possono essere corrette mediando misure per periodi di tempo più lunghi.

Coordinate geografiche

Il sistema di coordinate geografiche consente di individuare in maniera precisa e biunivoca ogni punto della superficie terrestre, la sua corrispondente rappresentazione sulla carta e viceversa. Esso è individuato dalla latitudine, dalla longitudine e dall'altitudine. La latitudine si definisce come il valore angolare dell'arco di meridiano compreso fra il punto e l'equatore, la longitudine è il valore angolare dell'arco di parallelo compreso fra quel punto e un meridiano di riferimento, infine l'altitudine o quota è definita rispetto ad un livello di riferimento, quello medio del mare, nei cui confronti può assumere valori positivi e negativi.

Trasformazioni di coordinate geografiche

È possibile operare la trasformazione da coordinate geografiche a cartesiane con le seguenti formule:

x=\left(N+h\right)\cos \varphi \ \cos \lambda

y=\left(N+h\right)\cos \varphi \ \sin \lambda

z=\left[N\left(1-e^{2}\right)+h\right]\sin \varphi

dove:

$N={\frac {a}{\sqrt[{2}]{(1-e^{2}(\sin \varphi )^{2})}}}$ (N raggio di curvatura detta Grannormale)

h è la quota ellissoidica, e è l'eccentricità ( $e^{2}={\frac {a^{2}-c^{2}}{a^{2}}}$ ) ed a è l'asse maggiore dell'ellissoide.

Bibliografia

sistemi di coordinate, su geomatica.como.polimi.it. URL consultato il 18 novembre 2016 (archiviato dall'url originale l'11 giugno 2016).
Elvio Lavagna, Geocartografia, Guida alla lettura delle carte geotopografiche, Zanichelli, 2014, ISBN 978-88-08-15789-8.

Voci correlate

Collegamenti esterni

sistemi di coordinate, su geomatica.como.polimi.it. URL consultato il 18 novembre 2016 (archiviato dall'url originale l'11 giugno 2016).