ערימה
במדעי המחשב, ערימה (באנגלית: Heap) היא מבנה נתונים בצורת עץ מכוון המקיים תכונה בסיסית, הנקראת תכונת הערימה.
לתכונת הערימה יש שני מודלים בסיסיים: ערימת מינימום וערימת מקסימום.
בערימת מקסימום המפתח של כל צומת בעץ קטן ממפתח אביו. כתוצאה מדרישה זו, הצומת בעל המפתח הגדול ביותר הוא תמיד השורש של העץ, וניתן למצוא אותו בסיבוכיות זמן , כלומר במספר פעולות קבוע, שאיננו תלוי במספר האיברים בערימה.
ב"ערימת מינימום", כל מפתח יהיה קטן ממפתחות בניו, כלומר המפתח הקטן ביותר יהיה שורש הערימה, ואלגוריתם פעולה על ערימה זו יפעל בצורה זהה לאלגוריתם הפועל על ערימת מקסימום.
דרישה זו היא הדרישה היחידה מערימות באופן כללי. ישנם סוגים ספציפיים של ערימות שבהם נוספות דרישות, המשפרות את תפקוד הערימה.
הערימות השונות הן המימושים היעילים ביותר של מבנה הנתונים המופשט תור עדיפויות.
דוגמה לשימוש של ערימה: כאשר יש בחדר מיון מטופלים בעלי רמת דחיפות שונה (לדוגמה: 100, 95, 90, 85 ו-80), נרצה להעניק את הטיפול הראשון למטופל הדחוף ביותר. ניתן להציג את כל הממתינים לטיפול בערימת מקסימום, כך שהמפתח של כל קודקוד יהיה רמת הדחיפות שלו.
בצורה זו כאשר המטופל הדחוף ביותר ייקרא לטיפול ויוסר מחדר המיון, נסיר את שורש הערימה באמצעות אלגוריתם הסרת שורש מערימה, והשורש החדש שייווצר יהיה הדחוף ביותר מבין הנותרים.
סוגי ערימות
[עריכת קוד מקור | עריכה]ערימה בינארית
[עריכת קוד מקור | עריכה] ערך מורחב – ערימה בינארית
ערך מורחב – ערימה בינארית
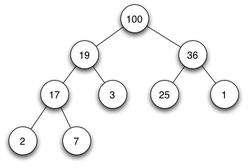
ערימה בינארית היא ערימה שמיוצגת באמצעות עץ בינארי, כלומר לכל צומת יש לכל היותר שני בנים. בנוסף לתכונת הערימה, היא מקיימת תכונה נוספת הנוגעת לצורתה:
- הערימה היא עץ כמעט שלם, כלומר היא מלאה לחלוטין בכל רמותיה פרט אולי לאחרונה המלאה מצד שמאל עד לנקודה מסוימת.
בזכות תכונה זו, דרך נוחה לייצג ערימה בינארית היא בתוך מערך, ובצורה קומפקטית בה אין צורך לשמור מצביעים מכל תא במערך לתאים המייצגים את בניו. בנו השמאלי של קודקוד יימצא באינדקס ובנו הימני באינדקס .
באופן דומה אביו של קודקוד יימצא באינדקס .
גישה זו מאפשרת את מימוש מיון ערימה, שממיין איברים תוך שימוש במקום קבוע (במקום להקצות כמות זיכרון נוספת התלויה בגודל הקלט) - כל המיון יתבצע בתוך המערך שבו נתונים האיברים.
ערימה מסוג זה ניתנת לבניה ממערך לא ממוין בסיבוכיות .
ערימה בינומית
[עריכת קוד מקור | עריכה] ערך מורחב – ערימה בינומית
ערך מורחב – ערימה בינומית
ערימה בינומית מיוצגת בתור אוסף של עצים בינומיים. ההגדרה המיוחדת של עצים בינומיים מבטיחה שהערימה תקיים, פרט לתכונת הערימה, תכונה נוספת:
- לכל דרגה נתונה זהה, קיים בערימה הבינומית לכל היותר עץ אחד שזוהי דרגת שורשו (כלומר, כל העצים בערימה הם מאורך שונה).
בשל תכונות אלו ערימה בינומית מסוגלת לאפשר מיזוג עם ערימה נוספת מסוגה בזמן מהיר.
ערימת פיבונאצ'י
[עריכת קוד מקור | עריכה] ערך מורחב – ערימת פיבונאצ'י
ערך מורחב – ערימת פיבונאצ'י
ערימות פיבונאצ'י ממומשות גם הן בתור אוסף של עצים, בדומה לערימות בינומיות, אך העצים אינם חייבים להיות עצים בינומיים. בשל כך ערימת פיבונאצ'י היא גמישה יותר, ומהירה יותר כאשר מתייחסים לסיבוכיות משוערכת של זמן הריצה של הפעולות שבה (כלומר, לא בודקים את הזמן שלוקחת פעולה בודדת, אלא את הזמן שלוקחת סדרה של פעולות).
ערימת פיבונאצ'י משמשת לשיפור זמן הריצה של אלגוריתמים דוגמת אלגוריתם דייקסטרה והאלגוריתם של פרים.
ייצוג ערימה במערך סטטי
[עריכת קוד מקור | עריכה]מקובל לייצג ערימה על ידי מערך סטטי (משתי סיבות עיקריות: טבעי וקל למימוש, יעיל בזיכרון וזמן ריצה).
כאמור בערימה (מקסימום) הנתון בכל קודקוד גדול שווה משני ילדיו. ערימה היא עץ שלם, פרט אולי לרמה האחרונה שבה העלים מתחילים משמאל לימין.
גודלו הלוגי של מערך יהיה n כמספר הקודקודים וישמר במשתנה נפרד heapSize.
- מערך בו השורש במקום 0.
- הילדים של קודקוד i באינדקסים 2i+1 (בן שמאלי), 2i+2 (בן ימני).
- האבא של קודקוד i באינדקס [i-1)/2)].
- העלים נמצאים באינדקסים: [n-1, n-2, n-3..., [n/2.
- מערך בו השורש במקום 1 (מתעלמים ממקום 0, שיטה זו מקלה על החישובים).
- הילדים של קודקוד i באינדקסים 2i (בן שמאלי), 2i+1 (בן ימני).
- האבא של קודקוד i באינדקס [i/2].
- העלים נמצאים באינדקסים: 1+[n, n-1, n-2..., [n/2.
מתכונות המערך יש אפשרות להתייחס למסלול בעץ המתאים לערימה בתור תת-מערך, זאת לצורך חישובים שונים על ידי כך שנעבור מהעלה לאביו וכך הלאה עד לשורש העץ, תת-המערך יהיה ממוין. לדוגמה: מצא את מיקומו של האיבר העומד להיכנס מבלי להכניסו.
ניתן גם לממש ערימה מדרגה K במערך סטטי באופן דומה.
ראו גם
[עריכת קוד מקור | עריכה]קישורים חיצוניים
[עריכת קוד מקור | עריכה]- Fredman, Michael Lawrence; Tarjan, Robert E. (1987). "Fibonacci heaps and their uses in improved network optimization algorithms" (PDF). Journal of the Association for Computing Machinery. 34 (3): 596–615. doi:10.1145/28869.28874.
| מבני נתונים | ||
|---|---|---|
| מבנים מופשטים | רשימה • מחסנית • קבוצה • מולטי קבוצה • תור • דו-תור • תור עדיפויות • מילון • מחרוזת • איחוד קבוצות זרות | |
| מימושים ליניאריים | מערך • מערך משונן • טבלת גיבוב • רשימה מקושרת • רשימת דילוגים • חוצץ | |
| גרפים ועצים | ערימה (בינארית • בינומית • פיבונאצ'י) • עץ חיפוש (עץ אדום שחור • עץ 2-3 • עץ 2-3-4) • עץ סיפות • עץ B • עץ +B • עץ AVL • עץ Splay • עץ BSP • עץ kd • עץ R • Trie • X-fast trie • טריי y מהיר• עץ WAVL | |
| הסתברותיים | מסנן בלום | |