מכפלה סקלרית

מכפלה סקלרית היא פעולה על שני וקטורים מהמרחב האוקלידי $\mathbb {R} ^{n}$ שמחזירה סקלר (ומכאן שמה). המכפלה הסקלרית מהווה מכפלה פנימית במרחב האוקלידי.

הגדרה פורמלית

המכפלה הסקלרית בין שני וקטורים ${\vec {\alpha }},{\vec {\beta }}$, מסומנת על ידי ${\vec {\alpha }}\cdot {\vec {\beta }}$ (יש ספרים המשתמשים בנקודת כפל עבה יותר, ולכן באנגלית מכפלה זו נקראת Dot product).

כשם שניתן לתאר וקטור במרחב באמצעות סדרת קואורדינטות או באמצעות אורכו וכיוונו, כך גם קיימות שתי הגדרות (שקולות) למכפלה הסקלרית המשתמשות במאפיינים אלה.

ההגדרה הגאומטרית

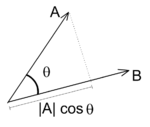
יהיו שני וקטורים ${\vec {\alpha }},{\vec {\beta }}$. מכפלתם הסקלרית שווה למכפלת אורכיהם (להכללת מונח האורך, עיינו בערך נורמה) וקוסינוס הזווית שביניהם. בסימנים:

${\vec {\alpha }}\cdot {\vec {\beta }}=\|\mathbf {\alpha } \|\|\mathbf {\beta } \|\cos(\alpha ,\beta )$.

בניגוד לזווית בין ישרים, שאינה יכולה לעלות על 90 מעלות, הזווית בין וקטורים יכולה גם להיות קהה ואז המכפלה הסקלרית תהיה שלילית.

ההגדרה האלגברית

במרחב וקטורי העמודה/שורה יהיו שני וקטורים מהצורה –

${\vec {\alpha }}=(a_{1},...,a_{n})$

${\vec {\beta }}=(b_{1},...,b_{n})$

מכפלתם הסקלרית תוגדר על ידי

$\langle \alpha ,\beta \rangle =a_{1}b_{1}+\dots +a_{n}b_{n}$

הגדרה זו כללית יותר מההגדרה הגאומטרית, כיוון שניתן להכלילה לממדים גדולים מ-$3$, שם מושג הזווית בין הווקטורים טעון הגדרה. למעשה ניתן להגדיר זווית בעזרת המכפלה הפנימית. כיוון שאי שוויון קושי-שוורץ מבטיח כי בכל ממד מתקיים $\left|{\vec {\alpha }}\cdot {\vec {\beta }}\right|\leq \left|{\vec {\alpha }}\right|\cdot \left|{\vec {\beta }}\right|$, ניתן להגדיר

$\cos \theta \,{\overset {\underset {\mathrm {def} }{}}{=}}\,{\frac {{\vec {\alpha }}\cdot {\vec {\beta }}}{|{\vec {\alpha }}|\cdot |{\vec {\beta }}|}}$.

תמיד ישנה זווית המקיימת משוואה זו, כיוון שהמנה תמיד קטנה או שווה בערכה המוחלט ל-$1$.

במקרה הפרטי של קואורדינטות קרטזיות במרחב תלת־ממדי, המכפלה הסקלרית נתונה על ידי

$\left(\alpha _{x}{\hat {x}}+\alpha _{y}{\hat {y}}+\alpha _{z}{\hat {z}}\right)\cdot \left(\beta _{x}{\hat {x}}+\beta _{y}{\hat {y}}+\beta _{z}{\hat {z}}\right)=\alpha _{x}\beta _{x}+\alpha _{y}\beta _{y}+\alpha _{z}\beta _{z}$

נוסחה זו נכונה עבור כל בסיס אורתונורמלי.

תכונות ומאפיינים

המכפלה הסקלרית היא ביליניארית (כלומר, ${\vec {A}}\cdot ({\vec {B}}+{\vec {C}})={\vec {A}}\cdot {\vec {B}}+{\vec {A}}\cdot {\vec {C}}$ ולכל סקלר $t$, $(t{\vec {A}})\cdot {\vec {B}}=t({\vec {A}}\cdot {\vec {B}})$) סימטרית (כלומר ${\vec {A}}\cdot {\vec {B}}={\vec {B}}\cdot {\vec {A}}$).

מכפלה סקלרית של שני וקטורים היא $0$ אם ורק אם הם ניצבים זה לזה, כיוון ש-$\cos 90^{\circ }=0$. ההכללה של תכונה זו במרחבי מכפלה פנימית כלליים היא האורתוגונליות (ביוונית, אורתוגונלי משמעו ניצב). כאשר המכפלה הפנימית בין שני וקטורים מתאפסת, הם נקראים וקטורים אורתוגונליים, או ניצבים.

משמעות

מכפלה סקלרית של וקטור מסוים בווקטור יחידה נותנת את ההטלה של הווקטור המסוים על אותו כיוון: ההיטל של וקטור ${\vec {B}}$ על ${\hat {A}}$ נתון על ידי ${\mbox{Projection}}=({\hat {A}}\cdot {\vec {B}}){\hat {A}}$ כאשר ה"כובע" מסמן וקטור יחידה.

שימושים

בפיזיקה, עבודה של כוח קבוע שווה למכפלה הסקלרית של הכוח בהעתק.

בתוכנה, ניתן לבדוק כמה קרובים שני וקטורים נורמלים (באורך $1$) להצביע לאותו הכיוון לפי המכפלה הסקלרית שלהם.

ראו גם

• מרחב וקטורי
• מכפלה פנימית (הכללה של מכפלה סקלרית)
• מכפלה וקטורית (מכפלה מסוג שונה ב-$\mathbb {R} ^{3}$)
• מכפלה מעורבת (מכפלה סקלרית של וקטור במכפלה וקטורית של שני וקטורים אחרים).
• דיברגנץ

קישורים חיצוניים

• מכפלה סקלרית, באתר MathWorld (באנגלית)