- Mathematiques
-
Mathématiques
Les mathématiques constituent un domaine de raisonnements logiques sur des concepts tels que les nombres, les structures et les transformations. Les mathématiques désignent aussi le domaine de recherche visant à développer ces connaissances, ainsi que la sciences par un rapport particulier au réel. Elles sont de nature purement intellectuelles, basées sur des vrais (c'est-à-dire que les axiomes ne sont pas soumis à l'expérience mais ils en sont souvent inspirés notamment dans le cas des mathématiques classiques) ou sur des postulats provisoirement admis. Un théorème, proposition, lemme, scholie ou vérité respecte une certaine structure rationnelle appelée sciences et dans différents domaines de la technique. C'est ainsi qu'[1].
Sommaire
Étymologie
Le terme « mathématique » vient du français, matematica en [2],[3].
La forme neutre de l'adjectif μαθηματικός a été substantivée en τα μαθηματικά (ta mathēmatiká) pour désigner les sciences mathématiques dans leur ensemble. Cette forme plurielle, utilisée par Cicéron (mathematica) puis en français et dans les autres langues européennes. Le singulier est parfois employé (« la mathématique » en français, mathematic en anglais), mais « le mot donne alors au contexte une teinte d'didactisme »[4].
Dans l'argot scolaire, le terme « mathématiques » est fréquemment Historique
Article détaillé : écriture. Le premier objet reconnu attestant de os d'Ishango datant de 20 000 ans avant notre ère[5],[6],[7]. Le développement des mathématiques en tant que connaissance transmise dans les premières commerce, la gestion des récoltes, la mesure des surfaces, la prédiction des événements astronomiques, et parfois l'exécution de rituels religieux.
écriture. Le premier objet reconnu attestant de os d'Ishango datant de 20 000 ans avant notre ère[5],[6],[7]. Le développement des mathématiques en tant que connaissance transmise dans les premières commerce, la gestion des récoltes, la mesure des surfaces, la prédiction des événements astronomiques, et parfois l'exécution de rituels religieux.
Les premiers développements mathématiques concernaient l'extraction des racines carrées, des racines cubiques, la résolution d'trigonométrie, le entiers naturels... Ils s'effectuèrent dans les civilisations babyloniennes, chinoises ou encore civilisation grecque, les mathématiques, influencées par les travaux antérieurs et les spéculations philosophiques, recherchent davantage d'abstraction. Les notions de axiomatique sont précisées. Deux branches se distinguent, l'géométrie. Au IIIe siècle av. J.-C., les [8] résument et ordonnent les connaissances mathématiques de la Grèce.
La chinoises et indiennes, notamment en matière de représentation des nombres[réf. nécessaire]. Les travaux mathématiques sont considérablement développés tant en trigonométrie (introduction des fonctions trigonométriques) qu'en analyse combinatoire, l'analyse numérique et l'algèbre polynomiale sont inventées et développées.
Durant la Renaissance européenne, une partie des textes arabes sont étudiés et traduits en latin. La recherche mathématique se concentre en Europe. Le Viète et Descartes. Leibniz, indépendamment, inventent le
 XVIIIe siècle et du XIXe siècle, les mathématiques connaissent de forts développements avec l'étude systématique des structures, à commencer par les Galois sur les équations polynomiales, et les Dedekind.
XVIIIe siècle et du XIXe siècle, les mathématiques connaissent de forts développements avec l'étude systématique des structures, à commencer par les Galois sur les équations polynomiales, et les Dedekind.
Le XIXe siècle voit avec Cantor le développement d'une théorie axiomatique sur tous les objets étudiés, soit la recherche des [réf. nécessaire]. Ce développement de l'axiomatique conduira plusieurs mathématiciens du XXe siècle à chercher à définir toutes les mathématiques à l'aide d'un langage : la logique.
Le XXe siècle a connu un fort développement en mathématiques avec une spécialisation des domaines, et la naissance ou le développement de nombreuses nouvelles branches (théorie de la mesure, théorie spectrale, topologie algébrique et informatique a eu un impact sur la recherche. D'une part, elle a facilité la communication et le partage des connaissances, d'autre part, elle a fourni un formidable outil pour la confrontation aux exemples. Ce mouvement a naturellement conduit à la modélisation et à la numérisation.
Domaines des mathématiques
Un découpage des mathématiques en deux, trois ou quatre domaines différents est couramment utilisé[réf. nécessaire] : algèbre et analyse, ou bien algèbre, analyse et géométrie, ou bien algèbre, analyse, probabilités. De tels découpages ne sont pas évidents et les frontières les séparant sont toujours mal définies. En effet, de nombreux résultats font appel à des compétences mathématiques variées. Le théorème de Wiles, établi en 1994, en est un exemple. Bien que formulé de manière dite arithmétique, la preuve nécessite de profondes compétences en analyse et en géométrie.
Domaines fondamentaux
L'algèbre est l'ensemble des méthodes mathématiques visant à étudier et développer les structures algébriques et à comprendre les relations qu'elles entretiennent entre elles. L'algèbre, au sens actuel, trouve historiquement ses origines dans la compréhension des équations polynomiales et dans les développements des méthodes de résolution : les recherches dans ces domaines ont suscité l'émergence des notions qui fondent la théorie des groupes, de la théorie de Galois ou encore de la analyse est la partie des mathématiques s'intéressant aux questions de régularité des applications d'une variable réelle ou complexe : on parle alors plus volontiers d'analyse réelle ou d'analyse complexe. En un sens élargi, elle englobe toutes les méthodes mathématiques qui s'y apparentent, et un certain nombre de méthodes pour comprendre et analyser les espaces de fonctions.
La probabilités tentent en un sens large de formaliser tout ce qui relève de l'aléatoire. Bien qu'anciennes, elles ont connu un renouveau avec la théorie de la mesure. La compréhension des lois aléatoires rendant compte au mieux des données déjà réalisées forme les statistiques.
Exemples de domaines transversaux
 mathématiques discrètes (associées à l'essor de l'groupes finis, probabilités discrètes, monoïdes, arithmétique élémentaire) utilise tout autant des méthodes analytiques que des méthodes algébriques, avancées, pour résoudre des problèmes qui peuvent souvent être énoncés de façon élémentaire.
mathématiques discrètes (associées à l'essor de l'groupes finis, probabilités discrètes, monoïdes, arithmétique élémentaire) utilise tout autant des méthodes analytiques que des méthodes algébriques, avancées, pour résoudre des problèmes qui peuvent souvent être énoncés de façon élémentaire.
- La topologie algébrique tend à associer à des objets géométriques de natures diverses des invariants de nature algébrique. Elle se situe donc à la frontière de la géométrie et de l'algèbre. Toutefois, pour des objets géométriques présentant une certaine structure analytique, ces invariants algébriques peuvent parfois se définir ou se comprendre en faisant uniquement appel à des outils essentiellement d'analyse. La majeure partie de la recherche en 2009 en topologie algébrique tend à oublier la structure topologique et à réduire les questions à des problèmes essentiellement d'algèbre.
- En un certain sens, les systèmes dynamiques se situent entre la géométrie, l'analyse et les probabilités. Ils tendent à comprendre de manière qualitative ce qui s'assimile à une loi d'évolution. Les objets étudiés relèvent de l'analyse (équations différentielles par exemples), des probabilités (itération d'une espaces homogènes). Le traitement qui y est consacré fait l'objet d'interprétations essentiellement de nature géométriques, tout en utilisant des outils avancés d'analyse fonctionnelle, de théorie des processus, de géométrie différentielle, etc. Des résultats d'arithmétique peuvent aussi être obtenus par des considérations relevant des systèmes dynamiques.
- La géométrie algébrique est l'exemple d'un domaine en un sens strict à la rencontre de l'algèbre et de la géométrie. Elle trouve ses origines dans les travaux sur la résolution des équations cubiques. Le premier objet d'étude de la géométrie algébrique est la variété algébrique, lieu d'annulation d'équations polynomiales : il a une signification à la fois algébrique et géométrique. Ce domaine connut un fort développement au XIXe siècle, avec notamment le théorème de Bézout. Les développements récents initiés par géométrie arithmétique.
- La théorie des opérateurs relève plutôt de l'analyse, ou encore de l'analyse fonctionnelle (par exemple, pour les problèmes de régularité des solutions d'équations aux dérivées partielles elliptiques, notamment le géométrie non commutative. Les objets d'études se trouvent être des généralisations d'algèbres d'opérateurs.
Mathématiques appliquées et mathématiques pures
 Simulation numérique d'un crash d'une voiture. - L'analyse numérique : domaine applicatif des mathématiques.
Simulation numérique d'un crash d'une voiture. - L'analyse numérique : domaine applicatif des mathématiques.
On fait parfois la distinction entre mathématiques pures et mathématiques appliquées :
- Les mathématiques pures ont pour objectif le développement des connaissances mathématiques pour elles-mêmes sans aucun intérêt a priori pour les applications, sans aucune motivation d'autres sciences. L'objet de la recherche mathématique peut ainsi être une meilleure compréhension d'une série d'exemples particuliers abstraits, sur lesquels s'appuie et se développe la réflexion mathématique, la généralisation d'un aspect d'une discipline ou la mise en évidence de liens entre diverses disciplines des mathématiques.
- Au contraire, les mathématiques appliquées sont la mise en œuvre des connaissances mathématiques pour les besoins de formalisme d'autres sciences (physique, biologie, Selon une boutade de [réf. nécessaire]
Les mathématiques appliquées, en un sens mal définies, comprennent entre autres l'analyse numérique, les statistiques appliquées et la théorie de l'optimisation mathématique. Certains domaines de recherche des mathématiques sont nées à la frontière avec d'autres sciences (voir ci-dessous).
Pratique mathématique
Activité de recherche
La recherche mathématique ne se limite pas qu'à la démonstration des théorèmes. L'une des méthodes les plus fructueuses de recherche mathématique est la mise en rapprochement de domaines a priori éloignés en mettant en lumière des phénomènes analogues (par exemple, la équations différentielles linéaires). Voir des phénomènes analogues se produire peut conduire à vouloir adapter des résultats d'un domaine des mathématiques à un autre, à reformuler des éléments de démonstration en termes équivalents, à tenter une espace vectoriel) qui regrouperait les deux domaines... Dans ce dernier cas, ce nouvel objet deviendrait alors un objet d'étude par lui-même. Dans certains cas, l'identification d'objets a priori différents devient nécessaire : le langage des catégories permet de faire ce genre de choses.
Une autre méthode de recherche est la confrontation aux exemples et aux cas particuliers. Cette confrontation peut permettre de réfuter des propriétés qu'on pensait ou espérait être vraies (géométrie riemannienne, l'étude des surfaces (donc des objets en dimension 2) et de leurs Anosov à formaliser le difféomorphisme d'Anosov, une transformation possédant d'intéressantes propriétés dynamiques.
Langage mathématique
Article détaillé : groupe, corps ou variété peuvent être empruntés et redéfinis pour désigner des objets mathématiques. Mais souvent des termes sont formés et introduits selon les besoins : topologie, symboles, les uns en rapport avec le implication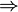 ou le connecteur unaire de négation
ou le connecteur unaire de négation  , d'autres en rapport avec le quantificateur universel
, d'autres en rapport avec le quantificateur universel 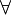 ou le quantificateur existentiel
ou le quantificateur existentiel 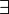 . La plupart des notations utilisées au XXIe siècle ont été introduites après le XVIIe siècle seulement.
. La plupart des notations utilisées au XXIe siècle ont été introduites après le XVIIe siècle seulement.
Il existe un langage mathématique qui décrit les mathématiques. En ce sens, on dit qu'il s'agit d'un métalangage : il s'agit de la logique mathématique.
Rapport des mathématiques avec les autres sciences
Les mathématiques entretiennent des rapports particuliers avec toutes les sciences, au sens large du terme. L'analyse de données (interprétation graphique, données statistiques...) fait appel à des compétences mathématiques variées. Mais des outils avancés de mathématiques interviennent dans les modélisations.
Toutes les sciences dites dures, à l'exception des mathématiques, tendent à une compréhension du monde réel. Cette compréhension passe par la mise en place d'un modèle, prenant en compte un certain nombre de paramètres considérés comme causes d'un phénomène. Ce modèle constitue un objet mathématique, dont l'étude permet une meilleure compréhension du phénomène étudié, éventuellement une prédiction qualitative ou quantitative quant à son évolution future.
La modélisation fait appel à des compétences relevant essentiellement de l'analyse et des probabilités, mais les méthodes algébriques ou géométriques s'avèrent utiles.
Mathématiques et physique
Les mathématiques sont nées d'une volonté de compréhension de l'espace ambiant : la géométrie naît de la modélisation de formes idéalisées, et l'arithmétique des besoins des gestions des quantités. Astronomie et géométrie différentielle est un outil essentiel sur lequel repose notamment la relativité générale, développée par le mathématicien Minkowski puis par le physicien Isaac Newton a-t-il développé le diffusion de la chaleur dans les corps, séries qui portent son nom, porte ouverte sur la théorie de Fourier ; ... Plus récemment, citons les problèmes de quantification géométrique, d'intégrales de Donaldson...
Un domaine de recherche spécifique, la physique mathématique, tend précisément à développer les méthodes mathématiques mises à l'usage de la physique.
Le lien étroit entre mathématiques et physique se reflète dans l'enseignement supérieur des mathématiques. L'enseignement de la physique fait appel à des cours de mathématiques pour physiciens ; et il n'est pas rare que les cursus de mathématiques dans les universités incluent une initiation facultative à la physique.
 Schéma de pendule.
Schéma de pendule.
Mathématiques et informatique
L'essor des techniques au XXe siècle a ouvert la voie à une nouvelle science, l'informatique théorique peuvent être considérés comme d'essence mathématique, d'autres branches de l'informatique faisant plutôt usage des mathématiques. Les nouvelles technologies de communication ont quant à elles ouvert la voie aux applications à des branches des mathématiques parfois très anciennes (cryptographie et théorie des codes.
En contrepartie, les sciences informatiques influencent l'évolution moderne des mathématiques.
Les mathématiques discrètes forment un domaine de recherche actuel des mathématiques visant à développer les méthodes utilisées en science informatique, incluant la théorie de la complexité, la théorie de l'information, la théorie des graphes... Parmi les problèmes ouverts, citons notamment le célèbre P=NP[9] en théorie de la complexité, qui fait partie des 7 problèmes du prix du millénaire. Celui qui arrivera à décider si P et NP sont différents ou égaux recevra un montant de 1 000 000 Les mathématiques et la biologie, la chimie et la géologie
La chaînes de Markov (théorie des processus discrets) ou par des équations différentielles couplées. Il en va de même pour l'évolution des génotypes : le principe de Hardy-Weinberg, souvent évoquée en génétique, relève de propriétés générales sur les processus à temps discret (existence de lois limites). Plus généralement, la phylogéographie fait appel à des modélisations probabilistes. De plus, la médecine use de tests (statistiques) pour comprendre la validité de tel ou tel traitement. Un domaine spécifique de recherche à la frontière de la biologie est né : la XXIe siècle, la macromolécule en biologie est variable et détermine son action. Cette modélisation fait appel à la polyèdre dont les distances et les angles sont fixés par les lois d'interaction.
Les géophysique, à savoir la géophysique mathématique. De même, la météorologie, l'océanographie et la planétologie sont grandes consommatrices de mathématiques car elles nécessitent des modélisations.
Rapport entre les mathématiques et les sciences humaines
Son rapport avec les sciences humaines se fait essentiellement par les statistiques et les probabilités, mais aussi par des stochastiques ou non, en économie et en finance (sociologie, psychologie, économie, gestion...).
Notamment, les mathématiques financières sont une branche des mathématiques appliquées visant à la compréhension de l'évolution des marchés financiers et de l'estimation des risques. Cette branche des mathématiques se développe à la frontière des probabilités et de l'analyse et use des statistiques.
Utilisation non scientifique
La mathématisation ou l'appel à des méthodes mathématiques ne justifie en aucun cas l'authenticité scientifique. En effet, les postulats d'une « pensée » peuvent être extrêmement problématiques, voire farfelus, mais s'ils sont de nature à être quantifiés, ils peuvent donner lieu à des calculs complexes.
Les astrologie statistique utilise les tests statistiques pour mettre en évidence d'éventuelles Choisnard et Gauquelin, menées à la marge de la recherche scientifique, n'ont en date de 2009 pas été productives et n'ont réussi à donner aucune preuve recevable d'un lien de cause à effet.
Dans l'essai polémique Sokal et économie mathématique. Le postulat fondamental de cette discipline est que l'activité économique peut se comprendre à partir d'un axiome de nature profit, et ce de façon rationnelle. Cette sorte de vision calcul individuel se transpose en calcul mathématique. Toutefois, certains sociologues, comme Bourdieu, et même certains économistes, refusent ce postulat de l'don, mais aussi dépendent d'autres enjeux dont l'intérêt financier n'est qu'une partie, ou tout simplement ne sont pas rationnelles. La mathématisation est donc selon eux un habillage permettant une valorisation scientifique de la matière.
Ceci dit, la modélisation mathématique en économie permet de percer à jour des mécanismes économiques qui n'auraient pu être découverts que très difficilement par une analyse « littéraire ». Par exemple, les explications des Mathématiques et philosophie
 Carl Friedrich Gauss : Regina Scientiarum[10] et le mot scientiarium signifie en réalité « des Fondements
Carl Friedrich Gauss : Regina Scientiarum[10] et le mot scientiarium signifie en réalité « des Fondements Article détaillé : logique comme outil pour démontrer des vérités organisées en théories. Une première analyse laisse espérer qu'une utilisation puissante de cet outil tellement sûr, une réduction toujours plus poussée des bases, les
Article détaillé : logique comme outil pour démontrer des vérités organisées en théories. Une première analyse laisse espérer qu'une utilisation puissante de cet outil tellement sûr, une réduction toujours plus poussée des bases, lesD'une part, en tant qu'activité humaine, les mathématiques s'éloignent du modèle d'une construction suivant scrupuleusement les lois de la logique et indépendante du réel. Citons un fait et un phénomène pour illustrer ceci. Tout d'abord, les démonstrations que rédigent les mathématiciens ne sont pas formalisées au point de suivre en détail les lois de la logique, car cela est impossible en un temps raisonnablement court. Comme pour n'importe quelle science. l'acceptation de la véracité d'une démonstration, et donc d'un théorème, repose in fine sur un La structure des révolutions scientifiques de Thomas Kuhn). L'avènement de l'[11].
Cependant l'activité mathématique est loin de se réduire à la recherche de démonstrations et à la vérification de celles-ci. La confiance que la communauté mathématique place dans un de ses membres qui propose un résultat nouveau intervient dans la réception qu'aura ce résultat, et ce d'autant plus s'il est inattendu, ou modifie la façon de voir les choses. On peut prendre pour exemple historique les controverses sur les XIXe siècle, durant lequel les travaux de Lobatchevsky ont été largement ignorés ; ou bien, dans un autre ordre d'idée, la difficulté de la réception des travaux du jeune républicain Cauchy[12]. La sociologie des mathématiques étudie de tels phénomènes (voir sociologie des sciences).
théorèmes d'incomplétude, démontrés par XXe siècle, montrent que, contrairement à ce qu'espérait Enseignement Article détaillé : mathématiques modernes, méthode de Moore, Impact culturel
Article détaillé : mathématiques modernes, méthode de Moore, Impact culturelExpression artistique
 Page couverture du Traité de l'harmonie réduite à ses principes naturels de fréquences fondamentales de vibration sont dans des rapports simples. Par exemple, l'octave est un doublement de fréquence, la quinte une multiplication par 3/2.
Page couverture du Traité de l'harmonie réduite à ses principes naturels de fréquences fondamentales de vibration sont dans des rapports simples. Par exemple, l'octave est un doublement de fréquence, la quinte une multiplication par 3/2.
Ce lien entre les fréquences et l'Traité de l'harmonie réduite à ses principes naturels de [13], compositeur baroque français et théoricien de la musique. Il repose en partie sur l'analyse des
Si la courbe tracée en rouge, qui suit les notes harmoniques, a une allure logarithmique, cela correspond au rapport entre deux phénomènes:
- d'une part, la représentation de la hauteur d'un son par notre fréquence du son (une fréquence double correspond toujours à la même « distance sonore » appelée octave).
- d'autre part, les fréquences harmoniques qui sont des multiples entiers de la fréquence fondamentale.
 beauté aux figures symétriques. Une symétrie d'une figure géométrique est, intuitivement, l'existence d'un motif de la figure qui se répète suivant une règle précise, tout en étant partiellement transformé. Mathématiquement, une symétrie est l'existence d'une action non triviale d'un isométrie, c'est-à-dire qui préserve les distances sur la figure. En d'autres termes, l'intuition de la règle est mathématiquement réalisée par le fait que c'est un groupe qui agit sur la figure, et le sentiment qu'une règle régit la symétrie est précisément dû à la structure algébrique de ce groupe.
beauté aux figures symétriques. Une symétrie d'une figure géométrique est, intuitivement, l'existence d'un motif de la figure qui se répète suivant une règle précise, tout en étant partiellement transformé. Mathématiquement, une symétrie est l'existence d'une action non triviale d'un isométrie, c'est-à-dire qui préserve les distances sur la figure. En d'autres termes, l'intuition de la règle est mathématiquement réalisée par le fait que c'est un groupe qui agit sur la figure, et le sentiment qu'une règle régit la symétrie est précisément dû à la structure algébrique de ce groupe.
Par exemple, le groupe lié à la symétrie miroir est l'ensemble
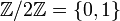 . Un test de Rorschach est une figure invariante par cette symétrie, de même qu'un papillon et plus généralement le corps des animaux, du moins en surface. Lorsqu'on dessine la surface de la mer, l'ensemble des vagues possède une symétrie par translation : bouger notre regard de la longueur séparant deux crêtes de vagues ne change pas la vue que l'on a de la mer. Un autre cas de symétrie, cette fois non isométrique et presque toujours seulement approximative, est celui présenté par les Vulgarisation
. Un test de Rorschach est une figure invariante par cette symétrie, de même qu'un papillon et plus généralement le corps des animaux, du moins en surface. Lorsqu'on dessine la surface de la mer, l'ensemble des vagues possède une symétrie par translation : bouger notre regard de la longueur séparant deux crêtes de vagues ne change pas la vue que l'on a de la mer. Un autre cas de symétrie, cette fois non isométrique et presque toujours seulement approximative, est celui présenté par les Vulgarisation
La vulgarisation mathématique a pour objectif de présenter les mathématiques en un langage dénué de termes techniques. Comme l'objet d'études des mathématiques n'est pas réel, elle use souvent d'un vocabulaire imagé, et de comparaisons ou analogies non rigoureuses, pour faire sentir l'idée des développements mathématiques. Parmi les ouvrages qui se fixent ce but, citons Oh, les maths de Yakov Perelman et Le livre qui rend fou de Raymond Smullyan. Toutefois, les mathématiques font rarement l'objet de vulgarisation dans des journaux écrits ou télévisés.
Littérature et filmographie
Si nombre de biographies portent sur les mathématiciens, les mathématiques sont un thème certes peu exploité dans la littérature ou la filmographie, mais présent.
Romans
- Plusieurs livres de Le Théorème du Perroquet
- Zéro, ou les cinq vies d'Aémer
- Le Démon des maths de Hans Magnus Enzensberger
- Mathématique du crime de Guillermo Martinez
Films
- Will Hunting
- Un homme d'exception, film de Ron Howard (2001)
- Pi, film de Darren Aronofsky (1998)
- La preuve irréfutable, (2005)
- Cube 2 et Crimes à Oxford.
Théatre
Pièces de théâtre
- Spécialistes de théâtre de sciences
- Le Théâtre scientifique de Louis Figuier, Fabienne Cardot, Revue Romantisme, 1989
- Théâtre et sciences, Le double fondateur, Jacques Baillon, L'Harmattan, 2002
- Le Théâtre de sciences, Michel Valmer, CNRS Éditions, 2006
- Science on stage, from Dr Faustus to Copenhagen, Kirsten Sheperd-Barr, Princeton University Press, 2006.
- Le Modèle scientifique dans le théâtre de Tom Stoppard, Liliane Campos, dans Epistémocritique, Revue d'études et de recherches sur la littérature et les savoirs, vol. II, 2008
Séries télévisées
- Numb3rs, série de Nicolas Falacci et Cheryl Heuton.
- Notes et références
- ↑ The Unreasonable Effectiveness of Mathematics in the Natural Sciences," Communications on Pure and Applied Mathematics 13(1): 1–14.
- ↑ (en) Oxford English Dictionary, article mathematic (accès restreint)
- ↑ The Oxford Dictionary of English Etymology, Oxford English Dictionary
- ↑ Colin, 1971 (à expliquer), cité à l'article mathématique du Trésor de la langue française
- ↑ Le Bâton d'Ishango, ↑ Le Bâton d'Ishango, MathWorld
- ↑ Les os incisés d'Ishango font naître la numération en Afrique, ↑ (en) Euclid's Elements (site interactif)
- ↑ (en) P=NP, ↑ Mathematics - Crystalinks
- ↑ Voir le numéro spécial de décembre 2008 des Notices of the American Mathematical Society consacré à la démonstration formelle
- ↑ Nicolas Bouleau, Actes du Groupe canadien d'études en didactique des mathématiques, page 24
- ↑ Traité de l'harmonie réduite à ses principes naturels, Paris, 1722, réédité en IBSN 2-86-563157-5 ou ISBN 2-05-100787-X
Voir aussi
Articles connexes
Liens externes
- Open Directory — Mathématiques
- Yahoo! Directory — Mathématiques
- PlanetMath.org : encyclopédie collaborative avec (en)
- Ressources en mathématiques (en)
- Encyclopaedia of Mathematics (en)
- Portail des mathématiques
- Portail sur les sciences
Catégorie : Mathématiques
Wikimedia Foundation. 2010.




