Anexo:Poliedros uniformes por el triángulo de Schwarz

Lista creada por Harold Scott MacDonald Coxeter de los poliedros uniformes wythoffianos degenerados, dando símbolos de Wythoff, figuras de vértices y descripciones usando los símbolos de Schläfli. Todos los poliedros uniformes y todos los poliedros uniformes Wythoffianos degenerados se enumeran en este artículo

Existen numerosas relaciones entre los poliedros uniformes. La construcción de Wythoff es capaz de generar casi todos los poliedros uniformes a partir de triángulos de Schwarz agudos y obtusos. Los números que se pueden usar para los lados de un triángulo de Schwarz agudo u obtuso no diedral que no conducen necesariamente a poliedros uniformes degenerados son 2, 3, 3/2, 4, 4/3, 5, 5/2, 5/3 y 5/4. Pero los números con numerador 4 y aquellos con numerador 5 no pueden aparecer juntos. También se puede usar 4/2, pero solo conduce a poliedros uniformes degenerados, ya que 4 y 2 tienen un factor común. Hay 44 triángulos de Schwarz de este tipo (5 con simetría tetraédrica, 7 con simetría octaédrica y 32 con simetría icosaédrica), que, junto con la familia infinita de triángulos de Schwarz diedrales, pueden formar casi todos los poliedros uniformes no degenerados. La construcción de Wythoff también puede generar muchos poliedros uniformes degenerados, con vértices, aristas o caras completamente coincidentes, y los que surgen de triángulos de Schwarz que no usan 4/2 también se dan en las tablas a continuación junto con sus elementos correspondientes no degenerados. Los triángulos de reflexión de Schwarz no se han incluido, ya que simplemente crean formas duplicadas o degeneradas; sin embargo, algunos se mencionan fuera de las tablas debido a su aplicación a tres de los poliedros romos.

Hay algunos poliedros uniformes no Wythoffianos que no pueden ser generados mediante triángulos de Schwarz. Sin embargo, la mayoría de ellos se pueden generar utilizando la construcción de Wythoff como recubrimientos dobles (los poliedros no Wythoffianos se recubren dos veces en lugar de una) o con varias caras coincidentes adicionales que deben descartarse para dejar no más de dos caras en cada borde (véase poliedro omnitruncado). Dichos poliedros están marcados con un asterisco en esta lista. Los únicos poliedros uniformes que no se generan mediante la construcción de Wythoff son el gran dirombicosidodecaedro y el gran dirrombidodecaedro birromo.

Cada mosaico de triángulos de Schwarz en una esfera puede cubrir la esfera solo una vez o, en cambio, puede enrollarse alrededor de la esfera un número entero de veces, cruzándose en el proceso. El número de veces que el teselado da vueltas alrededor de la esfera es la densidad del mosaico y se denota como μ.

Los nombres cortos de Jonathan Bowers para los poliedros, conocidos como acrónimos de Bowers, se utilizan en lugar de los nombres completos de los poliedros para ahorrar espacio. También se da el índice de Maeder. A excepción de los triángulos diédricos de Schwarz, los triángulos de Schwarz están ordenados por sus densidades.

Triángulos de Möbius y Schwarz

Hay 4 triángulos esféricos con ángulos π/p, π/q, π/r, donde (p q r) son números enteros: (Harold Scott MacDonald Coxeter, "Uniform polyhedra", 1954)

1. (2 2 r) - Diédrico
2. (2 3 3) - Tetraédrico
3. (2 3 4) - Octaédrico
4. (2 3 5) - Icosaédrico

Se denominan triángulos de Möbius.

Además, en los triángulos de Schwarz se considera que (p q r) son números racionales. Cada uno de estos se puede clasificar en uno de los 4 conjuntos anteriores.

Densidad (μ)	Diédrico	Tetraédrico	Octaédrico	Icosaédrico
d	(2 2 n/d)
1		(2 3 3)	(2 3 4)	(2 3 5)
2		(3/2 3 3)	(3/2 4 4)	(3/2 5 5), (5/2 3 3)
3		(2 3/2 3)		(2 5/2 5)
4			(3 4/3 4)	(3 5/3 5)
5		(2 3/2 3/2)	(2 3/2 4)
6		(3/2 3/2 3/2)		(5/2 5/2 5/2), (3/2 3 5), (5/4 5 5)
7			(2 3 4/3)	(2 3 5/2)
8				(3/2 5/2 5)
9				(2 5/3 5)
10				(3 5/3 5/2), (3 5/4 5)
11			(2 3/2 4/3)	(2 3/2 5)
13				(2 3 5/3)
14			(3/2 4/3 4/3)	(3/2 5/2 5/2), (3 3 5/4)
16				(3 5/4 5/2)
17				(2 3/2 5/2)
18				(3/2 3 5/3), (5/3 5/3 5/2)
19				(2 3 5/4)
21				(2 5/4 5/2)
22				(3/2 3/2 5/2)
23				(2 3/2 5/3)
26				(3/2 5/3 5/3)
27				(2 5/4 5/3)
29				(2 3/2 5/4)
32				(3/2 5/4 5/3)
34				(3/2 3/2 5/4)
38				(3/2 5/4 5/4)
42				(5/4 5/4 5/4)

Aunque un poliedro suele tener la misma densidad que el triángulo de Schwarz del que se genera, no siempre es así. En primer lugar, los poliedros que tienen caras que pasan por el centro del modelo (incluidos los hemipoliedros, el gran dirombicosidodecaedro y el gran dirrombidodecaedro birromo) no tienen una densidad bien definida. En segundo lugar, la distorsión necesaria para recuperar la uniformidad al cambiar un poliedro esférico a su equivalente plano puede empujar las caras a través del centro del poliedro y retroceder por el otro lado, cambiando la densidad. Esto sucede en los siguientes casos:

• El gran cuboctaedro truncado, 2 3 4/3 |. Mientras que el triángulo de Schwarz (2 3 4/3) tiene una densidad de 7, la recuperación de la uniformidad empuja los ocho hexágonos por el centro, dando una densidad |7 − 8| = 1, la misma que la del triángulo colunar de Schwarz (2 3 4) que comparte los mismos círculos máximos.
• El dodecadodecaedro truncado, 2 5/3 5 |. Mientras que el triángulo de Schwarz (2 5/3 5) tiene una densidad de 9, la recuperación de la uniformidad empuja a los doce decágonos por el centro, dando una densidad de |9 − 12| = 3, la misma que la del triángulo colunar de Schwarz (2 5/2 5) que comparte los mismos círculos máximos.
• Tres poliedros romos: el gran icosaedro | 2 3/2 3/2, el pequeno icosicosidodecaedro retrorromo | 3/2 3/2 5/2 y gran icosidodecaedro retrorromo | 2 3/2 5/3. Aquí las figuras de los vértices se han distorsionado en pentagramas o hexagramas en lugar de pentágonos o hexágonos, empujando todos los triángulos de la figura roma por el centro y dando densidades de |5 − 12| = 7, |22 − 60| = 38 y |23 − 60| = 37 respectivamente. Estas densidades son las mismas que las de los triángulos de Schwarz con ángulo "reflejo" colunar que no se incluyen arriba. Así, se puede considerar que el gran icosaedro proviene de (2/3 3 3) o (2 3 3/4), el pequeño icosicosidodecaedro retrorromo de (3 3 5/8) o (3 3/4 5/3), y el gran icosidodecaedro retrorromo de (2/3 3 5/2), (2 3/4 5/3), o (2 3 5/7). (Coxeter, "Poliedros uniformes", 1954)

Cuadro resumen

Las ocho formas para las construcciones de Wythoff a partir de un triángulo general (pqr). También se pueden crear "achatados parciales" (no se muestran en este artículo)

Las nueve formas reflexibles para las construcciones de Wythoff a partir de un cuadrilátero general (p q r s)

Hay siete puntos generadores con cada conjunto de p, q, r (y algunas formas especiales):

General				Triángulo rectángulo (r=2)
Descripción	Símbolo de Wythoff	Configuración de vértices	Diagrama de Coxeter	Símbolo de Wythoff	Configuración de vértices	Símbolo de Schläfli	Diagrama de Coxeter
Regular y cuasirregular	q | p r	(p.r)q		q | p 2	pq	{p,q}
	p | q r	(q.r)p		p | q 2	qp	{q,p}
	r | p q	(q.p)r		2 | p q	(q.p)²	t1{p,q}
Truncado y expandido	q r | p	q.2p.r.2p		q 2 | p	q.2p.2p	t0,1{p,q}
	p r | q	p.2q.r.2q		p 2 | q	p. 2q.2q	t0,1{q,p}
	p q | r	2r.q.2r.p		p q | 2	4.q.4.p	t0,2{p,q}
Enfrentado	p q r |	2r.2q.2p		p q 2 |	4.2q.2p	t0,1,2{p,q}
	p q r s |	2p.2q.-2p.-2q	-	p 2 r s |	2p.4.-2p.4/3		-
Achatado	| p q r	3.r.3.q.3.p		| p q 2	3.3.q.3.p	sr{p,q}
	| p q r s	(4.p.4.q.4.r.4.s)/2	-	-	-		-

Hay cuatro casos especiales:

• p q r
  s |: esta es una mezcla de p q r | y p q s |. Ambos símbolos p q r | y p q s | generan un poliedro de base común con algunas caras adicionales. La notación p q r
  s | representa entonces el poliedro base, formado por las caras comunes tanto a p q r | como a p q s |.
• | p q r: las formas achatadas (alternadas) reciben este símbolo que de otro modo no se usaría.
• | p q r s: una forma achatada única para el U75 que no es construible por Wythoff usando dominios fundamentales triangulares. Se incluyen cuatro números en este símbolo de Wythoff, ya que este poliedro tiene un dominio fundamental esférico tetragonal.
• | (p) q (r) s: una forma de achatado única para la figura de Skilling que no es construible por el procedimiento de Wythoff.

Esta tabla de conversión del símbolo de Wythoff a la configuración de vértice falla para los cinco poliedros excepcionales enumerados anteriormente, cuyas densidades no coinciden con las densidades de sus teselaciones de triángulos de Schwarz generadores. En estos casos se distorsiona mucho la figura de vértice para lograr uniformidad con caras planas: en los dos primeros casos es un triángulo obtuso en lugar de un triángulo acutángulo, y en los tres últimos es un pentagrama o hexagrama en lugar de un pentágono o hexágono, dando vueltas alrededor del centro dos veces. Esto da como resultado que algunas caras atraviesen el poliedro en comparación con las formas topológicamente equivalentes sin la distorsión de la figura de vértice y aparezcan como retrógradas en el otro lado.​

Diédrico (prismático)

En los triángulos diédricos de Schwarz, dos de los números son 2 y el tercero puede ser cualquier número racional estrictamente mayor que 1.

1. (2 2 n/d) – degenerado si mcd(n, d) > 1.

Muchos de los poliedros con simetría diédrica tienen caras digonales que los convierten en poliedros degenerados (por ejemplo, los diedros y los hosoedros). Las columnas de la tabla que solo dan poliedros uniformes degenerados no están incluidas: los casos degenerados especiales (solo en el triángulo de Schwarz (2 2 2)) están marcados con una cruz grande. Los antiprismas uniformes con una base {p} donde p < 3/2 no pueden existir porque sus figuras de vértices violarían la desigualdad triangular; estos también están marcados con una gran cruz. El antiprisma cruzado de 3/2 (trirp) es degenerado, es plano en el espacio euclidiano y también está marcado con una gran cruz. Los triángulos de Schwarz (2 2 n/d) se enumeran aquí solo cuando mcd(n, d) = 1, ya que de lo contrario solo dan como resultado poliedros uniformes degenerados.

La siguiente lista da todos los casos posibles donde n ≤ 6.

(p q r)	q r | p q.2p.r.2p	p r | q p. 2q.r.2q	p q r | 2r.2q.2p	| p q r 3.r.3.q.3.p
(2 2 2) (μ=1)	X	X	4.4.4 cubo 4-p	3.3.3 tet 2-ap
(2 2 3) (μ=1)	4.3.4 trip 3-p	4.3.4 trip 3-p	6.4.4 hip 6-p	3.3.3.3 oct 3-ap
(2 2 3/2) (μ=2)	4.3.4 trip 3-p	4.3.4 trip 3-p	6/2.4.4 2trip 6/2-p	X
(2 2 4) (μ=1)	4.4.4 cube 4-p	4.4.4 cube 4-p	8.4.4 op 8-p	3.4.3.3 squap 4-ap
(2 2 4/3) (μ=3)	4.4.4 cubo 4-p	4.4.4 cubo 4-p	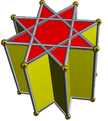8/3.4.4 stop 8/3-p	X
(2 2 5) (μ=1)	4.5.4 pip 5-p	4.5.4 pip 5-p	10.4.4 dip 10-p	3.5.3.3 pap 5-ap
(2 2 5/2) (μ=2)	4.5/2.4 stip 5/2-p	4.5/2.4 stip 5/2-p	10/2.4.4 2pip 10/2-p	3.5/2.3.3 stap 5/2-ap
(2 2 5/3) (μ=3)	4.5/2.4 stip 5/2-p	4.5/2.4 stip 5/2-p	10/3.4.4 stiddip 10/3-p	3.5/3.3.3 starp 5/3-ap
(2 2 5/4) (μ=4)	4.5.4 pip 5-p	4.5.4 pip 5-p	10/4.4.4 – 10/4-p	X
(2 2 6) (μ=1)	4.6.4 hip 6-p	4.6.4 hip 6-p	12.4.4 twip 12-p	3.6.3.3 hap 6-ap
(2 2 6/5) (μ=5)	4.6.4 hip 6-p	4.6.4 hip 6-p	12/5.4.4 stwip 12/5-p	X
(2 2 n) (μ=1)	4.n.4 n-p	4.n.4 n-p	2n.4.4 2n-p	3.n.3.3 n-ap
(2 2 n/d) (μ=d)	4.n/d.4 n/d-p	4.n/d.4 n/d-p	2n/d.4.4 2n/d-p	3.n/d.3.3 n/d-ap

Tetraédrico

En los triángulos tetraédricos de Schwarz, el numerador máximo permitido es 3.

#	(p q r)	q | p r (p.r)q	p | q r (q.r)p	r | p q (q.p)r	q r | p q.2p.r.2p	p r | q p. 2q.r.2q	p q | r 2r.q.2r.p	p q r | 2r.2q.2p	| p q r 3.r.3.q.3.p
1	(3 3 2) (µ=1)	3.3.3 tet U1	3.3.3 tet U1	3.3.3.3 oct U5	3.6.6 tut U2	3.6.6 tut U2	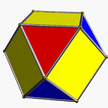4.3.4.3 co U7	4.6.6 toe U8	3.3.3.3.3 ike U22
2	(3 3 3/2) (µ=2)	(3.3.3.3.3.3)/2 2tet –	(3.3.3.3.3.3)/2 2tet –	(3.3.3.3.3.3)/2 2tet –	3.6.3/2.6 oho U3	3.6.3/2.6 oho U3	2(6/2.3.6/2.3) 2oct –	2(6/2.6.6) 2tut –	2(3.3/2.3.3.3.3) 2oct+8{3} –
3	(3 2 3/2) (µ=3)	3.3.3.3 oct U5	3.3.3 tet U1	3.3.3 tet U1	3.6.6 tut U2	2(3/2.4.3.4) 2thah U4*	3(3.6/2.6/2) 3tet –	2(6/2.4.6) cho+4{6/2} U15*	3(3.3.3) 3tet –
4	(2 3/2 3/2) (µ=5)	3.3.3 tet U1	3.3.3.3 oct U5	3.3.3 tet U1	3.4.3.4 co U7	3(6/2.3.6/2) 3tet –	3(6/2.3.6/2) 3tet –	4(6/2.6/2.4) 2oct+6{4} –	(3.3.3.3.3)/2 gike U53
5	(3/2 3/2 3/2) (µ=6)	(3.3.3.3.3.3)/2 2tet –	(3.3.3.3.3.3)/2 2tet –	(3.3.3.3.3.3)/2 2tet –	2(6/2.3.6/2.3) 2oct –	2(6/2.3.6/2.3) 2oct –	2(6/2.3.6/2.3) 2oct –	6(6/2.6/2.6/2) 6tet –	?

Octaédrico

En los triángulos octaédricos de Schwarz, el numerador máximo permitido es 4. También existen triángulos octaédricos de Schwarz que usan 4/2 como número, pero estos solo conducen a poliedros uniformes degenerados ya que 4 y 2 tienen un factor común.

#	(p q r)	q | p r (p.r)q	p | q r (q.r)p	r | p q (q.p)r	q r | p q.2p.r.2p	p r | q p. 2q.r.2q	p q | r 2r.q.2r.p	p q r | 2r.2q.2p	| p q r 3.r.3.q.3.p
1	(4 3 2) (µ=1)	4.4.4 cubo U6	3.3.3.3 oct U5	3.4.3.4 co U7	3.8.8 tic U9	4.6.6 toe U8	4.3.4.4 sirco U10	4.6.8 girco U11	3.3.3.3.4 snic U12
2	(4 4 3/2) (µ=2)	(3/2.4)4 oct+6{4} –	(3/2.4)4 oct+6{4} –	(4.4.4.4.4.4)/2 2cubo –	3/2.8.4.8 socco U13	3/2.8.4.8 socco U13	2(6/2.4.6/2.4) 2co –	2(6/2.8.8) 2tic –	?
3	(4 3 4/3) (µ=4)	(4.4.4.4.4.4)/2 2cubo –	(3/2.4)4 oct+6{4} –	(3/2.4)4 oct+6{4} –	3/2.8.4.8 socco U13	2(4/3.6.4.6) 2cho U15*	3.8/3.4.8/3 gocco U14	6.8.8/3 cotco U16	?
4	(4 2 3/2) (µ=5)	3.4.3.4 co U7	3.3.3.3 oct U5	4.4.4 cubo U6	3.8.8 tic U9	4.4.3/2.4 querco U17	4(4.6/2.6/2) 2oct+6{4} –	2(4.6/2.8) sroh+8{6/2} U18*	?
5	(3 2 4/3) (µ=7)	3.4.3.4 co U7	4.4.4 cubo U6	3.3.3.3 oct U5	4.6.6 toe U8	4.4.3/2.4 querco U17	3.8/3.8/3 quith U19	4.6/5.8/3 quitco U20	?
6	(2 3/2 4/3) (µ=11)	4.4.4 cubo U6	3.4.3.4 co U7	3.3.3.3 oct U5	4.3.4.4 sirco U10	4(4.6/2.6/2) 2oct+6{4} –	3.8/3.8/3 quith U19	2(4.6/2.8/3) groh+8{6/2} U21*	?
7	(3/2 4/3 4/3) (µ=14)	(3/2.4)4 = (3.4)4/3 oct+6{4} –	(4.4.4.4.4.4)/2 2cubo –	(3/2.4)4 = (3.4)4/3 oct+6{4} –	2(6/2.4.6/2.4) 2co –	3.8/3.4.8/3 gocco U14	3.8/3.4.8/3 gocco U14	2(6/2.8/3.8/3) 2quith –	?

Icosaédrico

En los triángulos icosaédricos de Schwarz, el numerador máximo permitido es 5. Además, el numerador 4 no se puede usar en absoluto en los triángulos icosaédricos de Schwarz, aunque se permiten los numeradores 2 y 3. (Si 4 y 5 pudieran aparecer juntos en algún triángulo de Schwarz, tendrían que hacerlo también en algún triángulo de Möbius; pero esto es imposible ya que (2 4 5) es un triángulo hiperbólico, no esférico).

#	(p q r)	q | p r (p.r)q	p | q r (q.r)p	r | p q (q.p)r	q r | p q.2p.r.2p	p r | q p. 2q.r.2q	p q | r 2r.q.2r.p	p q r | 2r.2q.2p	| p q r 3.r.3.q.3.p
1	(5 3 2) (µ=1)	5.5.5 doe U23	3.3.3.3.3 ike U22	3.5.3.5 id U24	3.10.10 tid U26	5.6.6 ti U25	4.3.4.5 srid U27	4.6.10 grid U28	3.3.3.3.5 snid U29
2	(3 3 5/2) (µ=2)	3.5/2.3.5/2.3.5/2 sidtid U30	3.5/2.3.5/2.3.5/2 sidtid U30	(310)/2 2ike –	3.6.5/2.6 siid U31	3.6.5/2.6 siid U31	2(10/2.3.10/2.3) 2id –	2(10/2.6.6) 2ti –	3.5/2.3.3.3.3 seside U32
3	(5 5 3/2) (µ=2)	(5.3/2)5 cid –	(5.3/2)5 cid –	(5.5.5.5.5.5)/2 2doe –	5.10.3/2.10 saddid U33	5.10.3/2.10 saddid U33	2(6/2.5.6/2.5) 2id –	2(6/2.10.10) 2tid –	2(3.3/2.3.5.3.5) 2id+40{3} –
4	(5 5/2 2) (µ=3)	(5.5.5.5.5)/2 gad U35	5/2.5/2.5/2.5/2.5/2 sissid U34	5/2.5.5/2.5 did U36	5/2.10.10 tigid U37	5.10/2.10/2 3doe –	4.5/2.4.5 raded U38	2(4.10/2.10) sird+12{10/2} U39*	3.3.5/2.3.5 siddid U40
5	(5 3 5/3) (µ=4)	5.5/3.5.5/3.5.5/3 ditdid U41	(3.5/3)5 gacid –	(3.5)5/3 cid –	3.10.5/3.10 sidditdid U43	5.6.5/3.6 ided U44	10/3.3.10/3.5 gidditdid U42	10/3.6.10 idtid U45	3.5/3.3.3.3.5 sided U46
6	(5/2 5/2 5/2) (µ=6)	(5/2)10/2 2sissid –	(5/2)10/2 2sissid –	(5/2)10/2 2sissid –	2(5/2.10/2)2 2did –	2(5/2.10/2)2 2did –	2(5/2.10/2)2 2did –	6(10/2.10/2.10/2) 6doe –	3(3.5/2.3.5/2.3.5/2) 3sidtid –
7	(5 3 3/2) (µ=6)	(3.5.3.5.3.5)/2 gidtid U47	(310)/4 2gike –	(3.5.3.5.3.5)/2 gidtid U47	2(3.10.3/2.10) 2seihid U49*	5.6.3/2.6 giid U48	5(6/2.3.6/2.5) 3ike+gad –	2(6.6/2.10) siddy+20{6/2} U50*	5(3.3.3.3.3.5)/2 5ike+gad –
8	(5 5 5/4) (µ=6)	(510)/4 2gad –	(510)/4 2gad –	(510)/4 2gad –	2(5.10.5/4.10) 2sidhid U51*	2(5.10.5/4.10) 2sidhid U51*	10/4.5.10/4.5 2did –	2(10/4.10.10) 2tigid –	3(3.5.3.5.3.5) 3cid –
9	(3 5/2 2) (µ=7)	(3.3.3.3.3)/2 gike U53	5/2.5/2.5/2 gissid U52	5/2.3.5/2.3 gid U54	5/2.6.6 tiggy U55	3.10/2.10/2 2gad+ike –	3(4.5/2.4.3) sicdatrid –	4.10/2.6 ri+12{10/2} U56*	3.3.5/2.3.3 gosid U57
10	(5 5/2 3/2) (µ=8)	(5.3/2)5 cid –	(5/3.3)5 gacid –	5.5/3.5.5/3.5.5/3 ditdid U41	5/3.10.3.10 sidditdid U43	5(5.10/2.3.10/2) ike+3gad –	3(6/2.5/2.6/2.5) sidtid+gidtid –	4(6/2.10/2.10) id+seihid+sidhid –	? (3|3 5/2) + (3/2|3 5)
11	(5 2 5/3) (µ=9)	5.5/2.5.5/2 did U36	5/2.5/2.5/2.5/2.5/2 sissid U34	(5.5.5.5.5)/2 gad U35	5/2.10.10 tigid U37	3(5.4.5/3.4) cadditradid –	10/3.5.5 quit sissid U58	10/3.4.10/9 quitdid U59	3.5/3.3.3.5 isdid U60
12	(3 5/2 5/3) (µ=10)	(3.5/3)5 gacid –	(5/2)6/2 2gissid –	(5/2.3)5/3 gacid –	2(5/2.6.5/3.6) 2sidhei U62*	3(3.10/2.5/3.10/2) ditdid+gidtid –	10/3.5/2.10/3.3 gaddid U61	10/3.10/2.6 giddy+12{10/2} U63*	3.5/3.3.5/2.3.3 gisdid U64
13	(5 3 5/4) (µ=10)	(5.5.5.5.5.5)/2 2doe –	(3/2.5)5 cid –	(3.5)5/3 cid –	3/2.10.5.10 saddid U33	2(5.6.5/4.6) 2gidhei U65*	3(10/4.3.10/4.5) sidtid+ditdid –	2(10/4.6.10) siddy+12{10/4} U50*	?
14	(5 2 3/2) (µ=11)	5.3.5.3 id U24	3.3.3.3.3 ike U22	5.5.5 doe U23	3.10.10 tid U26	3(5/4.4.3/2.4) gicdatrid –	5(5.6/2.6/2) 2ike+gad –	2(6/2.4.10) sird+20{6/2} U39*	5(3.3.3.5.3)/2 4ike+gad –
15	(3 2 5/3) (µ=13)	3.5/2.3.5/2 gid U54	5/2.5/2.5/2 gissid U52	(3.3.3.3.3)/2 gike U53	5/2.6.6 tiggy U55	3.4.5/3.4 qrid U67	10/3.10/3.3 quit gissid U66	10/3.4.6 gaquatid U68	3.5/3.3.3.3 gisid U69
16	(5/2 5/2 3/2) (µ=14)	(5/3.3)5 gacid –	(5/3.3)5 gacid –	(5/2)6/2 2gissid –	3(5/3.10/2.3.10/2) ditdid+gidtid –	3(5/3.10/2.3.10/2) ditdid+gidtid –	2(6/2.5/2.6/2.5/2) 2gid –	10(6/2.10/2.10/2) 2ike+4gad –	?
17	(3 3 5/4) (µ=14)	(3.5.3.5.3.5)/2 gidtid U47	(3.5.3.5.3.5)/2 gidtid U47	(3)10/4 2gike –	3/2.6.5.6 giid U48	3/2.6.5.6 giid U48	2(10/4.3.10/4.3) 2gid –	2(10/4.6.6) 2tiggy –	?
18	(3 5/2 5/4) (µ=16)	(3/2.5)5 cid –	5/3.5.5/3.5.5/3.5 ditdid U41	(5/2.3)5/3 gacid –	5/3.6.5.6 ided U44	5(3/2.10/2.5.10/2) ike+3gad –	5(10/4.5/2.10/4.3) 3sissid+gike –	4(10/4.10/2.6) did+sidhei+gidhei –	?
19	(5/2 2 3/2) (µ=17)	3.5/2.3.5/2 gid U54	(3.3.3.3.3)/2 gike U53	5/2.5/2.5/2 gissid U52	5(10/2.3.10/2) 2gad+ike –	5/3.4.3.4 qrid U67	5(6/2.6/2.5/2) 2gike+sissid –	6(6/2.4.10/2) 2gidtid+rhom –	?
20	(5/2 5/3 5/3) (µ=18)	(5/2)10/2 2sissid –	(5/2)10/2 2sissid –	(5/2)10/2 2sissid –	2(5/2.10/2)2 2did –	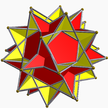2(5/2.10/3.5/3.10/3) 2gidhid U70*	2(5/2.10/3.5/3.10/3) 2gidhid U70*	2(10/3.10/3.10/2) 2quitsissid –	?
21	(3 5/3 3/2) (µ=18)	(310)/2 2ike –	5/2.3.5/2.3.5/2.3 sidtid U30	5/2.3.5/2.3.5/2.3 sidtid U30	5/2.6.3.6 siid U31	2(3.10/3.3/2.10/3) 2geihid U71*	5(6/2.5/3.6/2.3) sissid+3gike –	2(6/2.10/3.6) giddy+20{6/2} U63*	?
22	(3 2 5/4) (µ=19)	3.5.3.5 id U24	5.5.5 doe U23	3.3.3.3.3 ike U22	5.6.6 ti U25	3(3/2.4.5/4.4) gicdatrid –	5(10/4.10/4.3) 2sissid+gike –	2(10/4.4.6) ri+12{10/4} U56*	?
23	(5/2 2 5/4) (µ=21)	5/2.5.5/2.5 did U36	(5.5.5.5.5)/2 gad U35	5/2.5/2.5/2.5/2.5/2 sissid U34	3(10/2.5.10/2) 3doe –	3(5/3.4.5.4) cadditradid –	3(10/4.5/2.10/4) 3gissid –	6(10/4.4.10/2) 2ditdid+rhom –	?
24	(5/2 3/2 3/2) (µ=22)	5/2.3.5/2.3.5/2.3 sidtid U30	(310)/2 2ike –	5/2.3.5/2.3.5/2.3 sidtid U30	2(3.10/2.3.10/2) 2id –	5(5/3.6/2.3.6/2) sissid+3gike –	5(5/3.6/2.3.6/2) sissid+3gike –	10(6/2.6/2.10/2) 4ike+2gad –	(3.3.3.3.3.5/2)/2 sirsid U72
25	(2 5/3 3/2) (µ=23)	(3.3.3.3.3)/2 gike U53	5/2.3.5/2.3 gid U54	5/2.5/2.5/2 gissid U52	3(5/2.4.3.4) sicdatrid –	10/3.3.10/3 quit gissid U66	5(6/2.5/2.6/2) 2gike+sissid –	2(6/2.10/3.4) gird+20{6/2} U73*	(3.3.3.5/2.3)/2 girsid U74
26	(5/3 5/3 3/2) (µ=26)	(5/2.3)5/3 gacid –	(5/2.3)5/3 gacid –	(5/2)6/2 2gissid –	5/2.10/3.3.10/3 gaddid U61	5/2.10/3.3.10/3 gaddid U61	2(6/2.5/2.6/2.5/2) 2gid –	2(6/2.10/3.10/3) 2quitgissid –	?
27	(2 5/3 5/4) (µ=27)	(5.5.5.5.5)/2 gad U35	5/2.5.5/2.5 did U36	5/2.5/2.5/2.5/2.5/2 sissid U34	5/2.4.5.4 raded U38	10/3.5.10/3 quit sissid U58	3(10/4.5/2.10/4) 3gissid –	2(10/4.10/3.4) gird+12{10/4} U73*	?
28	(2 3/2 5/4) (µ=29)	5.5.5 doe U23	3.5.3.5 id U24	3.3.3.3.3 ike U22	3.4.5.4 srid U27	2(6/2.5.6/2) 2ike+gad –	5(10/4.3.10/4) 2sissid+gike –	6(10/4.6/2.4/3) 2sidtid+rhom –	?
29	(5/3 3/2 5/4) (µ=32)	5/3.5.5/3.5.5/3.5 ditdid U41	(3.5)5/3 cid –	(3.5/2)5/3 gacid –	3.10/3.5.10/3 gidditdid U42	3(5/2.6/2.5.6/2) sidtid+gidtid –	5(10/4.3.10/4.5/2) 3sissid+gike –	4(10/4.6/2.10/3) gid+geihid+gidhid –	?
30	(3/2 3/2 5/4) (µ=34)	(3.5.3.5.3.5)/2 gidtid U47	(3.5.3.5.3.5)/2 gidtid U47	(3)10/4 2gike –	5(3.6/2.5.6/2) 3ike+gad –	5(3.6/2.5.6/2) 3ike+gad –	2(10/4.3.10/4.3) 2gid –	10(10/4.6/2.6/2) 2sissid+4gike –	?
31	(3/2 5/4 5/4) (µ=38)	(3.5)5/3 cid –	(5.5.5.5.5.5)/2 2doe –	(3.5)5/3 cid –	2(5.6/2.5.6/2) 2id –	3(3.10/4.5/4.10/4) sidtid+ditdid –	3(3.10/4.5/4.10/4) sidtid+ditdid –	10(10/4.10/4.6/2) 4sissid+2gike –	5(3.3.3.5/4.3.5/4) 4ike+2gad –
32	(5/4 5/4 5/4) (µ=42)	(5)10/4 2gad –	(5)10/4 2gad –	(5)10/4 2gad –	2(5.10/4.5.10/4) 2did –	2(5.10/4.5.10/4) 2did –	2(5.10/4.5.10/4) 2did –	6(10/4.10/4.10/4) 2gissid –	3(3/2.5.3/2.5.3/2.5) 3cid –

No wythoffianos

Hemi formas

Estos poliedros (hemipoliedros) son generados como dobles revestimientos por la construcción de Wythoff. Si una figura generada por la construcción de Wythoff se compone de dos componentes idénticos, el operador "hemi" toma solo uno. El octaemioctaedro se incluye en la tabla para completar, aunque no se genera como un doble recubrimiento por la construcción de Wythoff.

3/2.4.3.4 thah U4 hemi(3 3/2 | 2)	4/3.6.4.6 cho U15 hemi(4 4/3 | 3)	5/4.10.5.10 sidhid U51 hemi(5 5/4 | 5)	5/2.6.5/3.6 sidhei U62 hemi(5/2 5/3 | 3)	5/2.10/3.5/3.10/3 gidhid U70 hemi(5/2 5/3 | 5/3)
	3/2.6.3.6 oho U3 hemi(?)	3/2.10.3.10 seihid U49 hemi(3 3/2 | 5)	5.6.5/4.6 gidhei U65 hemi(5 5/4 | 3)	3.10/3.3/2.10/3 geihid U71 hemi(3 3/2 | 5/3)

Formas reducidas

Estos poliedros se generan con caras adicionales mediante la construcción de Wythoff. Si la construcción de Wythoff genera una figura compuesta por dos o tres componentes no idénticos, el operador "reducido" elimina las caras adicionales (que deben especificarse) de la figura, dejando solo un componente.

Wythoff	Poliedro	Caras extra		Wythoff	Poliedro	Caras extra		Wythoff	Poliedro	Caras extra
3 2 3/2 |	4.6.4/3.6 cho U15	4{6/2}		4 2 3/2 |	4.8.4/3.8/7 sroh U18	8{6/2}		2 3/2 4/3 |	4.8/3.4/3.8/5 groh U21	8{6/2}
5 5/2 2 |	4.10.4/3.10/9 sird U39	12{10/2}		5 3 3/2 |	10.6.10/9.6/5 siddy U50	20{6/2}		3 5/2 2 |	6.4.6/5.4/3 ri U56	12{10/2}
5 5/2 3/2 |	3/2.10.3.10 seihid U49	id + sidhid		5 5/2 3/2 |	5/4.10.5.10 sidhid U51	id + seihid		5 3 5/4 |	10.6.10/9.6/5 siddy U50	12{10/4}
3 5/2 5/3 |	6.10/3.6/5.10/7 giddy U63	12{10/2}		5 2 3/2 |	4.10/3.4/3.10/9 sird U39	20{6/2}		3 5/2 5/4 |	5.6.5/4.6 gidhei U65	did + sidhei
3 5/2 5/4 |	5/2.6.5/3.6 sidhei U62	did + gidhei		3 5/3 3/2 |	6.10/3.6/5.10/7 giddy U63	20{6/2}		3 2 5/4 |	6.4.6/5.4/3 ri U56	12{10/4}
2 5/3 3/2 |	4.10/3.4/3.10/7 gird U73	20{6/2}		5/3 3/2 5/4 |	3.10/3.3/2.10/3 geihid U71	gid + gidhid		5/3 3/2 5/4 |	5/2.10/3.5/3.10/3 gidhid U70	gid + geihid
2 5/3 5/4 |	4.10/3.4/3.10/7 gird U73	12{10/4}

El tetrahemihexaedro (thah, U4) también es una versión reducida de la {3/2}-cúpula (cúpula triangular retrógrada, ratricu) de ídice {6/2}. Como tal, también puede denominarse "cupuloide triangular cruzado".

Muchos de los casos anteriores se derivan de poliedros omnitruncados degenerados p q r |. En estos supuestos, se pueden generar dos casos degenerados distintos p q r | y p q s | a partir de los mismos p y q; el resultado tiene caras {2p}, {2q} y {2r} o {2s} coincidentes respectivamente. Ambos producen los mismos poliedros uniformes no degenerados cuando se descartan las caras coincidentes, lo que Coxeter simbolizó como p q r
s |. Estos casos se enumeran a continuación:

4.6.4/3.6 cho U15 2 3 3/2 3/2 |	4.8.4/3.8/7 sroh U18 2 3 3/2 4/2 |	4.10.4/3.10/9 sird U39 2 3 3/2 5/2 |	6.10/3.6/5.10/7 giddy U63 3 5/3 3/2 5/2 |
6.4.6/5.4/3 ri U56 2 3 5/4 5/2 |	4.8/3.4/3.8/5 groh U21 2 4/3 3/2 4/2 |	4.10/3.4/3.10/7 gird U73 2 5/3 3/2 5/4 |	10.6.10/9.6/5 siddy U50 3 5 3/2 5/4 |

En el rombihexaedro pequeño y grande, se usa la fracción 4/2 a pesar de no estar en términos mínimos. Mientras que 2 4 2 | y 2 4/3 2 | representan un solo prisma octogonal u octagrámico respectivamente, 2 4 4/2 | y 2 4/3 4/2 | representan tres de esos prismas, que comparten algunas de sus caras cuadradas (precisamente las que se duplicaron para producir {8/2}'s). Estos {8/2} aparecen con simetría rotacional cuádruple y no doble, lo que justifica el uso de 4/2 en lugar de 2.​

Otras formas

Estos dos poliedros uniformes no pueden generarse en absoluto mediante la construcción de Wythoff. Este es el conjunto de poliedros uniformes comúnmente descritos como "no Wythoffianos". En lugar de los dominios fundamentales triangular del Wythoffi

un poliedro uniforme, estos dos poliedros tienen dominios fundamentales cuadriláteroal.

La figura de Skilling no recibe un índice en la lista de Maeder debido a que es un poliedro uniforme "exótico", con ridges (aristas en el caso 3D) completamente coincidentes. Esto también es cierto para algunos de los poliedros degenerados incluidos en la lista anterior, como el Pequeño complex icosidodecaedro. Esta interpretación de que las aristas son coincidentes permite que estas figuras tengan dos caras por arista: no duplicar las aristas les daría 4, 6, 8, 10 o 12 caras reunidas en una arista, figuras que normalmente se excluyen como poliedros uniformes. La figura de Skilling tiene 4 caras que se encuentran en algunos bordes.

(p q r s)	| p q r s (4.p. 4.q.4.r.4.s)/2	| (p) q (r) s (p3.4.q.4.r3.4.s.4)/2
(3/2 5/3 3 5/2)	(4.3/2.4.5/3.4.3.4.5/2)/2 gidrid U75	(3/23.4.5/3.4.33.4.5/2.4)/2 gidisdrid Skilling

Figura de vértice de | 3 5/3 5/2	Gran dodecicosidodecaedro romo	Gran dirombicosidodecaedro	Figura de vértice de | 3/2 5/3 3 5/2
Gran dirrombidodecaedro birromo	Compuesto de veinte octaedros	Compuesto de veinte tetrahemihexahedros	Figura de vértice de |(3/2) 5/3 (3) 5/2

Ambos poliedros especiales pueden derivarse del gran dodecicosidodecaedro romo, | 3 5/3 5/2 (U64). Este es un poliedro achatado quiral, pero sus pentagramas aparecen en pares coplanares. Combinando una copia de este poliedro con su enantiomorfo, los pentagramas coinciden y pueden eliminarse. Como las aristas de la figura de vértice de este poliedro incluyen tres lados de un cuadrado, con el cuarto lado aportado por su enantiomorfo, se concluye que el poliedro resultante es de hecho el compuesto de veinte octaedros. Cada uno de estos octaedros contiene un par de caras paralelas que se derivan de un triángulo completamente simétrico de | 3 5/3 5/2, mientras que los otros tres provienen de los triángulos romos originales de | 3 5/3 5/2. Además, cada octaedro puede ser reemplazado por el tetrahemihexaedro con las mismas aristas y vértices. Tomando los triángulos completamente simétricos en el octaedro, los pentagramas coincidentes originales en el gran dodecicosidodecaedro romo, y los cuadrados ecuatoriales del tetrahemihexaedro juntos producen el gran dirombicosidodecaedro (el monstruo de Miller).​ Si se toman los triángulos romos del octaedro, se obtiene el gran dirombidodecaedro romo (figura de Skilling).​

Teselaciones euclídeas

Los únicos triángulos planos que recubren el plano una vez son (3 3 3), (4 2 4) y (3 2 6): corresponden respectivamente al triángulo equilátero, el triángulo isósceles rectángulo 45-45-90 , y el triángulo rectángulo 30-60-90. De ello se deduce que cualquier triángulo plano que recubra el plano varias veces debe construirse a partir de múltiples copias de uno de estos. La única posibilidad que tesela el plano dos veces es el triángulo isósceles obtuso 30-30-120 (3/2 6 6) = (6 2 3) + (2 6 3). Cada triángulo cuenta dos veces con orientaciones opuestas, con un punto de bifurcación en los vértices de 120°.​

No se acepta el teselado {∞,2} formado por dos apeirógonos, porque sus caras se encuentran en más de una arista. Aquí ∞' denota la contraparte retrógrada de ∞.

Las formas nombradas degeneradas son:

• chatit: compuesto de 3 mosaicos hexagonales + mosaico triangular
• chata: compuesto de 3 mosaicos hexagonales + mosaicos triangulares + cubiertas dobles de apeirógonos en todas las secuencias de aristas
• cha: compuesto de 3 mosaicos hexagonales + cubiertas dobles de apeirógonos en todas las secuencias de aristas
• cosa: mosaico cuadrado + cubiertas dobles de apeirógonos en todas las secuencias de arista

(p q r)	q | p r (p.r)q	p | q r (q.r)p	r | p q (q.p)r	q r | p q.2p.r.2p	p r | q p.2q.r.2q	p q | r 2r.q.2r.p	p q r | 2r.2q.2p	| p q r 3.r.3.q.3.p
(6 3 2)	6.6.6 hexat	3.3.3.3.3.3 trat	3.6.3.6 that	3.12.12 toxat	6.6.6 hexat	4.3.4.6 srothat	4.6.12 grothat	3.3.3.3.6 snathat
(4 4 2)	4.4.4.4 squat	4.4.4.4 squat	4.4.4.4 squat	4.8.8 tosquat	4.8.8 tosquat	4.4.4.4 squat	4.8.8 tosquat	3.3.4.3.4 snasquat
(3 3 3)	3.3.3.3.3.3 trat	3.3.3.3.3.3 trat	3.3.3.3.3.3 trat	3.6.3.6 that	3.6.3.6 that	3.6.3.6 that	6.6.6 hexat	3.3.3.3.3.3 trat
(∞ 2 2)	—	—	—	—	4.4.∞ azip	4.4.∞ azip	4.4.∞ azip	3.3.3.∞ azap
(3/2 3/2 3)	3.3.3.3.3.3 trat	3.3.3.3.3.3 trat	3.3.3.3.3.3 trat	∞-covered {3}	∞-covered {3}	3.6.3.6 that	[degenerado]	?
(4 4/3 2)	4.4.4.4 squat	4.4.4.4 squat	4.4.4.4 squat	4.8.8 tosquat	4.8/5.8/5 quitsquat	∞-covered {4}	4.8/3.8/7 qrasquit	?
(4/3 4/3 2)	4.4.4.4 squat	4.4.4.4 squat	4.4.4.4 squat	4.8/5.8/5 quitsquat	4.8/5.8/5 quitsquat	4.4.4.4 squat	4.8/5.8/5 quitsquat	3.3.4/3.3.4/3 rasisquat
(3/2 6 2)	3.3.3.3.3.3 trat	6.6.6 hexat	3.6.3.6 that	[degenerado]	3.12.12 toxat	3/2.4.6/5.4 qrothat	[degenerado]	?
(3 6/5 2)	3.3.3.3.3.3 trat	6.6.6 hexat	3.6.3.6 that	6.6.6 hexat	3/2.12/5.12/5 quothat	3/2.4.6/5.4 qrothat	4.6/5.12/5 quitothit	?
(3/2 6/5 2)	3.3.3.3.3.3 trat	6.6.6 hexat	3.6.3.6 that	[degenerado]	3/2.12/5.12/5 quothat	3.4.6.4 srothat	[degenerado]	?
(3/2 6 6)	(3/2.6)6 chatit	(6.6.6.6.6.6)/2 2hexat	(3/2.6)6 chatit	[degenerado]	3/2.12.6.12 shothat	3/2.12.6.12 shothat	[degenerado]	?
(3 6 6/5)	(3/2.6)6 chatit	(6.6.6.6.6.6)/2 2hexat	(3/2.6)6 chatit	∞-covered {6}	3/2.12.6.12 shothat	3.12/5.6/5.12/5 ghothat	6.12/5.12/11 thotithit	?
(3/2 6/5 6/5)	(3/2.6)6 chatit	(6.6.6.6.6.6)/2 2hexat	(3/2.6)6 chatit	[degenerado]	3.12/5.6/5.12/5 ghothat	3.12/5.6/5.12/5 ghothat	[degenerado]	?
(3 3/2 ∞)	(3.∞)3/2= (3/2.∞)3 ditatha	(3.∞)3/2= (3/2.∞)3 ditatha	—	6.3/2.6.∞ chata	[degenerado]	3.∞.3/2.∞ tha	[degenerado]	?
(3 3 ∞')	(3.∞)3/2= (3/2.∞)3 ditatha	(3.∞)3/2= (3/2.∞)3 ditatha	—	6.3/2.6.∞ chata	6.3/2.6.∞ chata	[degenerado]	[degenerado]	?
(3/2 3/2 ∞')	(3.∞)3/2= (3/2.∞)3 ditatha	(3.∞)3/2= (3/2.∞)3 ditatha	—	[degenerado]	[degenerado]	[degenerado]	[degenerado]	?
(4 4/3 ∞)	(4.∞)4/3 cosa	(4.∞)4/3 cosa	—	8.4/3.8.∞ gossa	8/3.4.8/3.∞ sossa	4.∞.4/3.∞ sha	8.8/3.∞ satsa	3.4.3.4/3.3.∞ snassa
(4 4 ∞')	(4.∞)4/3 cosa	(4.∞)4/3 cosa	—	8.4/3.8.∞ gossa	8.4/3.8.∞ gossa	[degenerado]	[degenerado]	?
(4/3 4/3 ∞')	(4.∞)4/3 cosa	(4.∞)4/3 cosa	—	8/3.4.8/3.∞ sossa	8/3.4.8/3.∞ sossa	[degenerado]	[degenerado]	?
(6 6/5 ∞)	(6.∞)6/5 cha	(6.∞)6/5 cha	—	6/5.12.∞.12 ghaha	6.12/5.∞.12/5 shaha	6.∞.6/5.∞ 2hoha	12.12/5.∞ hatha	?
(6 6 ∞')	(6.∞)6/5 cha	(6.∞)6/5 cha	—	6/5.12.∞.12 ghaha	6/5.12.∞.12 ghaha	[degenerado]	[degenerado]	?
(6/5 6/5 ∞')	(6.∞)6/5 cha	(6.∞)6/5 cha	—	6.12/5.∞.12/5 shaha	6.12/5.∞.12/5 shaha	[degenerado]	[degenerado]	?

El teselado 6 6/5 | ∞ se genera como una doble cubierta por la construcción de Wythoff:

6.∞.6/5.∞ hoha hemi(6 6/5 | ∞)

También hay algunos mosaicos con el símbolo mixto p q r
s |:

4.12.4/3.12/11 sraht 2 6 3/2 3 |

4.12/5.4/3.12/7 graht 2 6/5 3/2 3 |

8/3.8.8/5.8/7 sost 4/3 4 2 ∞ |

12/5.12.12/7.12/11 huht 6/5 6 3 ∞ |

Así mismo, se conocen algunos mosaicos no Wythoffianos:

3.3.3.4.4 etrat

3.3.3.4/3.4/3 retrat

No se demuestra que el conjunto de mosaicos uniformes del plano sea completo, a diferencia del conjunto de poliedros uniformes. Los mosaicos de arriba representan todos los encontrados por Coxeter, Longuet-Higgins y Miller en su artículo de 1954 sobre poliedros uniformes.

Conjeturaron que las listas estaban completas: esto fue probado por Sopov en 1970 para los poliedros uniformes, pero no ha sido probado para las teselaciones uniformes. De hecho, Branko Grünbaum, J. C. P. Miller y G. C. Shephard enumeran quince teselaciones uniformes no Wythoffianas más en Teselaciones uniformes con teselas huecas (1981):​

4.8.8/3.4/3.∞ rorisassa	4.8/3.8.4/3.∞ rosassa	4.8.4/3.8.4/3.∞ rarsisresa (2 formas)	4.8/3.4.8/3.4/3.∞ rassersa (2 formas)
3/2.∞.3/2.∞.3/2.4.4	3/2.∞.3/2.∞.3/2.4/3.4/3
3/2.∞.3/2.∞.3/2.12/5.6.12/5	3/2.∞.3/2.∞.3/2.12/7.6/5.12/7	3/2.∞.3/2.∞.3/2.12.6/5.12	3/2.∞.3/2.∞.3/2.12/11.6/5.12/11	3/2.∞.3/2.4/3.4/3.3/2.4/3.4/3	3/2.∞.3/2.4.4.3/2.4.4
3/2.∞.3/2.4.4.3/2.4/3.4/3

Hay dos mosaicos cada uno para las figuras de vértice 4.8.4/3.8.4/3.∞ y 4.8/3.4.8/3.4/3.∞; usan los mismos conjuntos de vértices y aristas, pero tienen un conjunto diferente de cuadrados. También existe un tercer mosaico para cada una de estas dos figuras de vértice que es solo seudouniforme (todos los vértices se parecen, pero vienen en dos órbitas de simetría). Por lo tanto, para las teselaciones euclídeas, la configuración de los vértices no determina únicamente la teselación.​ En las imágenes que figuran a continuación, los cuadrados incluidos con bordes horizontales y verticales están marcados con un punto central. Un solo cuadrado tiene los bordes resaltados.​

• 
  Uniforme (grupo del papel pintado p4m)
• 
  Uniforme (grupo del papel pintado p4g)
• 
  Seudouniforme

Grünbaum, Miller y Shephard también enumeran 33 mosaicos uniformes que usan zigzags (apeirógonos oblicuos) como caras, diez de los cuales son familias que tienen un parámetro libre (el ángulo del zigzag). En ocho casos este parámetro es continuo; en dos, es discreto.​

Teselaciones hiperbólicas

El conjunto de triángulos que recubren el plano hiperbólico es infinito. Además, en el espacio hiperbólico el dominio fundamental no tiene por qué ser un símplex. En consecuencia, no se puede dar una lista completa de las teselaciones uniformes del plano hiperbólico.

Incluso cuando se restringe a mosaicos convexos, es posible encontrar múltiples mosaicos con la misma configuración de vértices: consúltese, por ejemplo, teselado cuadrado de orden-6 achatado.​

A continuación figura una pequeña muestra de casos convexos (que no involucran caras o vértices ideales):

(p q r)	q | p r (p.r)q	p | q r (q.r)p	r | p q (q.p)r	q r | p q.2p.r.2p	p r | q p.2q.r.2q	p q | r 2r.q.2r.p	p q r | 2r.2q.2p	| p q r 3.r.3.q.3.p
(7 3 2)	7.7.7 heat	3.3.3.3.3.3.3 hetrat	3.7.3.7 thet	3.14.14 theat	6.6.7 thetrat	4.3.4.7 srothet	4.6.14 grothet	3.3.3.3.7 snathet
(8 3 2)	8.8.8 ocat	3.3.3.3.3.3.3.3 otrat	3.8.3.8 toct	3.16.16 tocat	6.6.8 totrat	4.3.4.8 srotoct	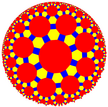4.6.16 grotoct	3.3.3.3.8 snatoct
(5 4 2)	5.5.5.5 peat	4.4.4.4.4 pesquat	4.5.4.5 tepet	4.10.10 topeat	5.8.8 topesquat	4.4.4.5 srotepet	4.8.10 grotepet	3.3.4.3.5 stepet
(6 4 2)	6.6.6.6 shexat	4.4.4.4.4.4 hisquat	4.6.4.6 tehat	4.12.12 toshexat	6.8.8 thisquat	4.4.4.6 srotehat	4.8.12 grotehat	3.3.4.3.6 snatehat
(5 5 2)	5.5.5.5.5 pepat	5.5.5.5.5 pepat	5.5.5.5 peat	5.10.10 topepat	5.10.10 topepat	4.5.4.5 tepet	4.10.10 topeat	3.3.5.3.5 spepat
(6 6 2)	6.6.6.6.6.6 hihat	6.6.6.6.6.6 hihat	6.6.6.6 shexat	6.12.12 thihat	6.12.12 thihat	4.6.4.6 tehat	4.12.12 toshexat	3.3.6.3.6 shihat
(4 3 3)	3.4.3.4.3.4 dittitecat	3.3.3.3.3.3.3.3 otrat	3.4.3.4.3.4 dittitecat	3.8.3.8 toct	6.3.6.4 sittitetrat	6.3.6.4 sittitetrat	6.6.8 totrat	3.3.3.3.3.4 stititet
(4 4 3)	3.4.3.4.3.4.3.4 ditetetrat	3.4.3.4.3.4.3.4 ditetetrat	4.4.4.4.4.4 hisquat	4.8.3.8 sittiteteat	4.8.3.8 sittiteteat	6.4.6.4 tehat	6.8.8 thisquat	3.3.3.4.3.4 stitetet
(4 4 4)	4.4.4.4.4.4.4.4 osquat	4.4.4.4.4.4.4.4 osquat	4.4.4.4.4.4 osquat	4.8.4.8 teoct	4.8.4.8 teoct	4.8.4.8 teoct	8.8.8 ocat	3.4.3.4.3.4 dittitecat

Bibliografía

• Coxeter, Harold Scott MacDonald; Longuet-Higgins, M. S.; Miller, J. C. P. (1954). «Uniform polyhedra». Philosophical Transactions of the Royal Society of London. Series A. Mathematical and Physical Sciences (The Royal Society) 246 (916): 401-450. ISSN 0080-4614. JSTOR 91532. MR 0062446. S2CID 202575183. doi:10.1098/rsta.1954.0003.  [1]
• Skilling, J. (1974). «The complete set of uniform polyhedra». Philosophical Transactions of the Royal Society of London. Series A. Mathematical and Physical Sciences (The Royal Society) 278 (1278): 111-135. ISSN 1364-503X. S2CID 122634260. doi:10.1098/rsta.1975.0022.  [2]

Enlaces externos

Richard Klitzing: Poliedros por:

• Simetría de grupos puntuales
• Complejidad
• Triángulos de Schwarz parte 1, parte 2
• Zvi Har'El: Solución uniforme para poliedros uniformes

• Datos: Q6644217