Draft:Ball on a String, the Ultimate Summary
| Submission declined on 25 January 2024 by AngusWOOF (talk). This submission is not suitable for Wikipedia. Please read "What Wikipedia is not" for more information. This submission reads more like an essay than an encyclopedia article. Submissions should summarise information in secondary, reliable sources and not contain opinions or original research. Please write about the topic from a neutral point of view in an encyclopedic manner.
Where to get help
How to improve a draft
You can also browse Wikipedia:Featured articles and Wikipedia:Good articles to find examples of Wikipedia's best writing on topics similar to your proposed article. Improving your odds of a speedy review To improve your odds of a faster review, tag your draft with relevant WikiProject tags using the button below. This will let reviewers know a new draft has been submitted in their area of interest. For instance, if you wrote about a female astronomer, you would want to add the Biography, Astronomy, and Women scientists tags. Editor resources
|  |
| Submission declined on 25 January 2024 by Qcne (talk). This submission is not adequately supported by reliable sources. Reliable sources are required so that information can be verified. If you need help with referencing, please see Referencing for beginners and Citing sources. This submission reads more like an essay than an encyclopedia article. Submissions should summarise information in secondary, reliable sources and not contain opinions or original research. Please write about the topic from a neutral point of view in an encyclopedic manner. Declined by Qcne 10 months ago. |  |
 Comment: Wikipedia is not a research paper site. AngusW🐶🐶F (bark • sniff) 23:22, 25 January 2024 (UTC)
Comment: Wikipedia is not a research paper site. AngusW🐶🐶F (bark • sniff) 23:22, 25 January 2024 (UTC)
 Comment: Wikipedia cannot be used as a source, which leaves just one source.Is this draft original research? Qcne (talk) 13:23, 25 January 2024 (UTC)
Comment: Wikipedia cannot be used as a source, which leaves just one source.Is this draft original research? Qcne (talk) 13:23, 25 January 2024 (UTC)
1) Introduction
[edit]Ball on a String classic exercise[1] in physics manuals is intended to show an example of Second Euler Law, often referred to as the "Law of Conservation of Angular Momentum":
(1) [2]
Where is the Angular Momentum, time and the total external torque acting on the spinning (rigid) object.
In the Ball on a String classic exercise a ball of mass is attached to a string and rotates on a horizontal frictionless plane , balancing ball weight, at an angular initial speed around a vertical axis while an arbitrary force is pulling the string downward causing the ball to close its distance from rotation axis and shortening same string from its initial lenght to some such as in a given time interval :

Along the ball the suppport plane further simplifying assumptions are made (along others):
- Infinitely rigid, massless, unflexible string.
- No air drag.
- No friction along string axis.
- Pulling force parallel (coincident) to rotation axis.
Only under the assumptions above thus being zero the total external torque exerted on the ball (), (1) can be rewritten as:
(2) [4]which defines CoAM as and thus , stating equivalence between two distinct distances and .
Being the ball Moment of Inertia (MoI) with respect to rotation axis at a distance and MoI after string retraction, thus angular momentum , (2) becomes:
(3) , then not changing in the () time interval and thus which is, skipping steps:
(4) the final angular speed of the ball after string retraction.
We could have come to the same conclusion also by expressing (2) as:
(5) (balance between Coriolis force torque with respect to the rotation axis and rotational inertia) which also is:
(6) that, after integration of both members between and is exactly (4).
Equations (2) (6) expresses CoAM again in the ideal only case where any disturbance comes to alter ball dynamics thus any assumption like the support plane and (1.,2.,3.,4.) leading external torque to be are equivalent to a perpetual motion assumption. CoAM is instead and generally a tendency, when , , , : like in outer space.
3) Conservation of Rotational Energy (CoRE) within PMA
[edit]To better analyse the Ball on a String system still in the PMA case we shall account for both ball angular speed about the rotation axis z and its linear velocity along the string while the latter is retracted. Total kinetic energy being:
(7) [5](which could be also written directly adding the kinetic energy from both ball linear speed components, and : which is (7) ).
At the instant string is steady, thus , the ball carries only rotational energy:
(8)
Instead at the generic instant the string is being retracted thus and the Ball on a String system kinetic energy is still expressed by (7).
Energy conservation principle (CoE) can be thus written such as (7)=(8), :
(9) meaning:
(10) generic angular speed change during string retraction.
Equation (10) is different from classic (4), being the angular speed proportional not to the square of retraction ratio but to its square root.
If is the final angular speed obtained through (10) CoE model and the one obtained by means of (4) CoAM model, it will always be:
(11)
And it has to be further noted that:
(12) <<
and:
(13)
So, for slow retracting speeds equation (9) becomes:
(14) expressing conservation of rotational energy (CoRE), otherwise not conserved for not negligible retracting speeds where (9) CoE applies. Equation (14) means a ball angular speed while string is retracted as:
(15) that may be accepted instead of (4) under the proper assumption.
4) Differences between PMA CoAM / CoRE / CoE
[edit]Below plot shows a comparison between predicted angular speed from CoRE and CoAM model (equation (4) and (15)) when string is retracted:


Surely CoRE (15) equation shows closer to realistic predictions than CoAM cause the first accounts for the entire Ball on a String system kinetics (rotational and linear) while the latter only rotational, the same applies for the not negligible case, where we use (10) CoE instead of CoRE.
5) Realistic Ball on a String, Removing PMA, SAM Failed CoAM
[edit]Removing the ball support plane but keeping (1.,2.,3.,4.) so letting same ball to move also in the vertical (string bending angle ) plane resembles a more realistic Ball on a String system that can be modeled by a simple Spinning Atwood Machine (SAM):

Which can be assessed by a standard Lagrange[6][7]approach to write SAM Equation of Motion (EoM):
(16)
Where is same as above the angular speed of the ball around the z axis while being the ball angular speed in the vertical plane and the same speed of the ball along the string during retraction.
First equation shows ball dynamics along the string axis, second the ball rotational equilibrium about rotation axis z and the third same rotational equilibrium in the vertical plane. It may be noticed that if the second equation can be rewritten as then exactly (6) and thus CoAM (4). But the latter CoAM shows only about the z axis, there's not linear momentum conservation (along string axis) nor CoAM in the vertical plane where ball weight is not equilibrated after removing the support plane assumption, so in (1).
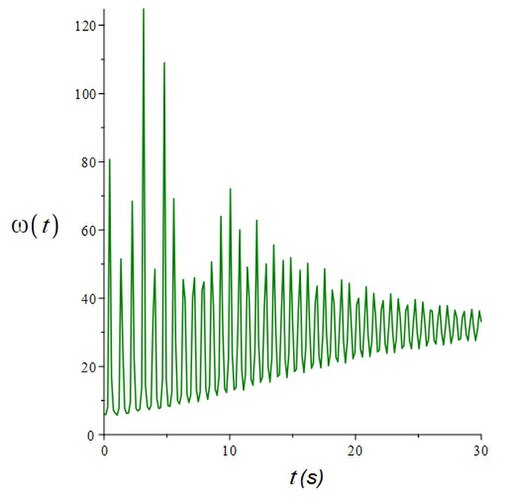
Which means that SAM model of the Ball on a String does not preserve angular momentum (it's only a tendency, as above) as it can be shown by numeric (16) EoM numeric integration plot:

And when introducing air drag (only on the z axis spinning motion), string friction and stiffness, staying the latter unflexible and massless, also z axis CoAM (second (16) equation) vanishes:
(17)
Where ( string Young Modulus, string cross section, string lenght) and ( air density, drag coefficient for a streamlined ball to reduce turbulences).
5.1) The Electric Motor
[edit]It has to be noted that equations (16) and (17) are written without considering the torque of the electric motor driving SAM: EoM describes the condition in which (motor off) and the counterweight is released, when the distance of the ball from the rotation axis could decrease (string to "shorten") or increase (string to "lenghten") following the balance between centrifugal force and same counterweight.
5.2) SAM EoM Details
[edit]First equation of system (16) is about forces equilibrium along the string: inertial force of two masses , then centrifugal acceleration in the vertical plane and = component of centrifugal force due to ball rotation around z axis projected on the string direction.
Second equation shows torques equilibrium around the z axis, where:
- is the inertial torque due to angular acceleration .
- the torque of Coriolis force[8][9] (velocity component ).
- the torque of Coriolis force (velocity component ).
Third equation represents torque equilibrium on the vertical plane:
- is the inertial torque.
- torque of Coriolis force.
- torque of the centrifugal force.
- weight of the ball.



5.3) Simplified SAM CoAM (PMA is Back).
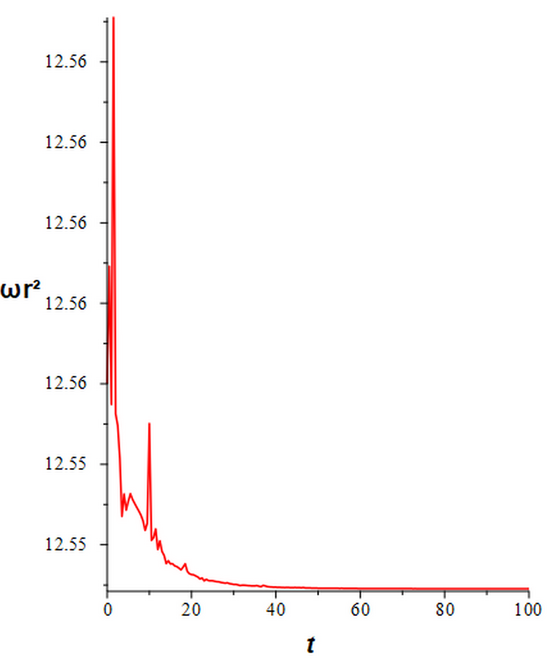
[edit]Assuming back the ball's spinning on the support plane so that , its weight is balanced, no air drag, and a new friction coefficient (16)-(17) EoM become:
(18)
And below the plots of predicted dynamics of the simplfied SAM and CoAM condition met:



5.3.1) Out of Curiosity: The Unreachable Simplified SAM (USS)
[edit]Considering the centrifugal force component (green in the force diagarm below) balancing ball weigth on the tangent to the trajectory we get the equilibrium condition:
(19) .

For the elevation angle of the SAM ball to be exactly it must be ( ) in (19), thus same SAM ball can't be spinning on a horizontal plane circular trajectory and its string being orthogonal to rotation axis regardless the magnitude of .
It is also graphically evident that when weight component while centrifugal force component being progressively impossible for them to balance.
6) Keeled Ball on a String (KBS), Helped CoAM
[edit]As seen, the classic Ball on a String exercise is proposed being the string pulled by a vertical while the ball is spinning on the horizontal plane.
What if on the contrary we assume an horizontal and a vertical spinning plane?

Below a force diagram of KBS:

EoM of KBS are, always under (1.,2.,3.) assumptions:
(20)
Which cleary resemble EoM (18) with the difference of the weight component preventing CoAM: external torques on the rotation axis are indeed different than zero () thus won't preserve as a consequence of (1). It will preserve only when an electric motor is set along to continuously balance with its torque the ball weight torque (thus it can't be switched off).
7) About Ball on a String Example
[edit]Simpler, more intuitive, mechanical systems needing less assumptions to prove CoAM are (have always been) available (online too). Both conservation of linear and angular momentum are just tendencies from the general principle stating that each object set in motion tends to preserve its state of motion, but obviously and due to the conservation (transformation) of energy principle, no state of motion can last forever (ad infinitum).
References
[edit]- ^ Sacchetti, Andrea (2023-10-03). "On the ball on a string demonstration of angular momentum conservation". European Journal of Physics. 44 (6): 065004. Bibcode:2023EJPh...44f5004S. doi:10.1088/1361-6404/acf6b9. ISSN 0143-0807.
- ^ "9.6: Conservation of Angular Momentum". Physics LibreTexts. 2018-04-12. Retrieved 2024-01-25.
- ^ "9.6: Conservation of Angular Momentum". Physics LibreTexts. 2018-04-12. Retrieved 2024-01-25.
- ^ "9.6: Conservation of Angular Momentum". Physics LibreTexts. 2018-04-12. Retrieved 2024-01-25.
- ^ "6.4: Rotational Kinetic Energy". Physics LibreTexts. 2021-08-13. Retrieved 2024-01-25.
- ^ Bordoni, Piero Giorgio (1995). Lezioni di Meccanica Razionale (5th ed.). Milan: Veschi (published 1994). ISBN 978-8841335208.
- ^ "Lagrangian Mechanics" (PDF).
- ^ "Coriolis force | Description, Examples, & Facts | Britannica". www.britannica.com. Retrieved 2024-01-25.
- ^ "Coriolis Force". sciencedemonstrations.fas.harvard.edu. Retrieved 2024-01-25.
- ^ "Drawing Free-Body Diagrams". www.physicsclassroom.com. Retrieved 2024-01-25.