Minimalkostenkombination
Unter einer Minimalkostenkombination (engl. lowest-cost combination oder least-cost combination) versteht man in Produktionstheorie bzw. Mikroökonomie eine optimale Kombination zweier Produktionsfaktoren.[1] Das Problem diese Kombination zu bestimmen wird auch kostenminimierende Inputwahl genannt.[2]
Bei einer Minimalkostenkombination kann gemäß dem Wirtschaftlichkeitsprinzip entweder eine gegebene Menge zu minimalen Kosten hergestellt oder bei gegebenem Kostenbudget die hergestellte Menge maximiert werden.[3] Eine Minimalkostenkombination ist damit die Umsetzung des ökonomischen Prinzips im Produktionsbereich einer Unternehmung: ein gegebenes Ziel mit geringstem Aufwand realisieren (Minimumversion) oder mit gegebenem Aufwand möglichst viel zu erreichen (Maximumversion).[4]
Zur Vereinfachung werden oft nur zwei Inputfaktoren betrachtet, etwa Arbeit und Kapital. Eine entsprechende Frage könnte lauten: Wie viel Arbeit und Kapital sind jeweils einzusetzen, um einen bestimmten Output zu minimalen Kosten zu erzielen?
Substitutionale Faktoreinsatzbedingungen
[Bearbeiten | Quelltext bearbeiten]
Substitutionalität erlaubt es, einen bestimmten Output durch verschiedene effiziente Kombinationen von Produktionsfaktoren zu erstellen. Dies wird im Allgemeinen angenommen, da viele Faktoren in gewissem Maße substituierbar sind. Die Form oder Existenz der Minimalkostenkombinationen hängt also stark von der Form der zugrundeliegenden Produktionsfunktion ab. Zur Vereinfachung wird weiter angenommen, dass die Ertragsisoquante konvex sei. Wäre diese linear oder konkav, wäre die optimale Kombination eine Randlösung.[5]
In diesem Fall liegt eine Minimalkostenkombination vor (notwendige Bedingung), wenn sich die Grenzproduktivitäten je zweier Faktoren zueinander verhalten wie deren Preise: die sogenannte Grenzrate der technischen Substitution entspricht also dem Verhältnis der Faktorpreise.
Zahlenbeispiel
[Bearbeiten | Quelltext bearbeiten]Im Zwei-Güter-Fall sei die Produktionsfunktion gegeben durch (Typ: Cobb-Douglas-Funktion). Die Preise der Inputfaktoren betragen und . Das Verhältnis der Ableitungen der Produktionsfunktion nach ihren Inputfaktoren soll jenem Verhältnis der jeweiligen Preise der Inputfaktoren entsprechen:
- .
Daraus ergibt sich:
Für eine entsprechende Budgetrestriktion (Isokostengerade, Gesamtkosten betragen bspw. 182) können nun die optimalen Mengen von und berechnet werden:
- .
Dieses Optimierungsproblem kann auch mit Hilfe von Lagrange-Multiplikatoren gelöst werden.
Limitationale Produktionsfunktion
[Bearbeiten | Quelltext bearbeiten]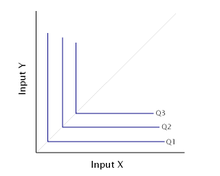
Im Falle einer einzelnen limitationalen Funktion, können alle Outputmengen jeweils nur mit einer einzigen Faktorkombination realisiert werden. Diese ist dann auch die Minimalkostenkombination.[6] Da die Isoquante hier lediglich aus einem Punkt besteht, ist die Frage der Bestimmung einer Minimalkostenkombination eigentlich nicht vorhanden, da es nur diese eine effiziente Produktion gibt.[7] In diesem Fall, wäre die Kombination durch die technischen Produktionsbedingungen determiniert. Nur effiziente Kombinationsprozesse können auch kostenminimal sein.[8]
Stehen zwei oder mehr limitationale Funktionen zur Wahl, die alle das gleiche Ergebnis liefern, so können sie kombiniert und substituiert werden. Stehen beispielsweise die beiden linear-limitationalen Funktionen und zur Verfügung so ist es möglich mit jeder der beiden Prozesse je ein Produkt herzustellen, was einer Faktorsubstitution faktisch gleichkommt.
Expansionspfad
[Bearbeiten | Quelltext bearbeiten]
Im Isoquantendiagramm ist eine Minimalkostenkombination als Tangentialpunkt von Isoquante und Isokostengerade zu erkennen. Die Verbindungslinie der Minimalkostenkombinationen für unterschiedliche Produktionsniveaus heißt Expansionspfad.
Graphisch bedeutet dies, dass man mit geringen Kosten beginnend die Kosten langsam ansteigen lässt. Dadurch verschiebt sich die Isokostengerade weiter und weiter nach außen und tangiert eine Isoquante nach der anderen. Die Tangentialpunkte werden markiert und verbunden. Im Ergebnis entsteht ein Expansionspfad (in der Abbildung rot eingezeichnet).[9]
Literatur
[Bearbeiten | Quelltext bearbeiten]- Günter Fandel: Produktion. I. Springer-Verlag, Berlin 2007. Kapitel IV Das kostentheoretische Auswahlproblem: Die Minimalkostenkombination. ISBN 978-3-540-73140-5, S. 233 ff.
Einzelnachweise
[Bearbeiten | Quelltext bearbeiten]- ↑ Bofinger, Peter. Grundzüge der Volkswirtschaftslehre: eine Einführung in die Wissenschaft von Märkten. Pearson Deutschland GmbH, 2011. S. 102.
- ↑ Pindyck, Robert S. Mikroökonomie. Pearson Deutschland GmbH, 2009. S. 316.
- ↑ Minimalkostenkombination – Artikel im Gabler Wirtschaftslexikon.
- ↑ Minimalkostenkombination – Artikel bei mikrooekonomie.de.
- ↑ Joachim Schwalbach: Produktionstheorie. Vahlen, 2014, S. 23.
- ↑ Corsten: Produktionswirtschaft. 6. Auflage, S. 91f.
- ↑ Wollenberg, Klaus. Volkswirtschaftslehre: Einführung und Grundlagen mit Lösungen/von Rainer Fischbach und Klaus Wollenberg. Vol. 1. Oldenbourg Verlag, 2007. S. 234.
- ↑ Joachim Schwalbach: Produktionstheorie. Vahlen, 2014, S. 21.
- ↑ Expansionspfad – Artikel bei www.mikrooekonomie.de.
Weblinks
[Bearbeiten | Quelltext bearbeiten]- Minimalkostenkombination – Artikel im Gabler Wirtschaftslexikon
- Minimalkostenkombination – Artikel bei mikrooekonomie.de
- Minimalkostenkombination – kurze Beschreibung