Elektron
 Belirli enerji seviyelerinde (aşağıya doğru artarak: n-1, 2, 3,...) ve açısal momentumlardaki (sağa doğru artarak: s, p, d,...) bir hidrojen atomu elektronunun dalga fonksiyonları. Daha parlak olan bölgeler elektronun pozisyonu için daha yüksek olasılık genliğini gösterir. | |
| Bileşim | Temel parçacık |
|---|---|
| Aile | Fermiyon |
| Nesil | Birinci |
| Etkileşim(ler) | Kütleçekim, elektromanyetik, zayıf |
| Sembol | e- , β- |
| Antiparçacık | Pozitron |
| Teorileştirme | Richard Laming (1838-1851) Johnstone Stoney (1874) ve diğerleri |
| Keşif | J. J. Thomson (1897) |
| Kütle | 9,1093837015(28)×10-31 kg 5,48579909065(16)×10-4 u [1822,888486209(53)]-1 u[a] 0,51099895000(15) MeV/c2 |
| Ortalama yaşam süresi | Kararlı (>6,6×1028 yıl) |
| Elektrik yükü | -1 e[b] -1,602176634×10-19 C |
| Manyetik moment | 9,2847647043(28)×10-24 J/T -1.00115965218128(18) μB |
| Spin | 12 |
| Zayıf izospin | LH: -12, RH: 0 |
| Zayıf hiperyük | LH: -1, RH: -2 |
Elektron (
e-
veya
β-
simgeleri ile gösterilir), eksi bir temel elektrik yüküne sahip bir atomaltı parçacıktır. Lepton parçacık ailesinin ilk nesline aittir ve bileşenleri ya da bilinen bir alt yapıları olmadığından genellikle temel parçacıklar olarak düşünülürler. Kütleleri, protonların yaklaşık olarak 1/1836'sı kadardır. Kuantum mekaniği özellikleri arasında, indirgenmiş Planck sabiti (ħ) biriminde ifade edilen, yarım tam sayı değerinde içsel bir açısal momentum (spin) vardır. Fermiyon olmasından ötürü, Pauli dışarlama ilkesi gereğince iki elektron aynı kuantum durumunda bulunamaz. Temel parçacıkların tamamı gibi hem parçacık hem dalga özelliklerini gösterir ve bu sayede diğer parçacıklarla çarpışabilir ya da kırınabilirler.
Elektronlar; elektrik, manyetizma, kimya ve ısı iletkenliği gibi çeşitli fizik fenomeninde temel rol oynamalarının yanı sıra; kütleçekimsel, elektromanyetik ve zayıf kuvvetlerde de yer alır. Yüklü olmalarından dolayı kendilerini çevreleyen bir elektrik alanı bulunur ve gözlemciye bağlı hareket etmesi sonucunda manyetik alan meydana gelir. Diğer kaynaklar tarafından oluşturulan manyetik alanlar, Lorentz kuvveti kanunu gereğince elektronların hareketlerini etkiler. Elektronlar, radyasyona uğramaları veya hızlandırılmaları durumlarında enerjiyi foton şeklinde emerler. Laboratuvar aletleri ile elektronların tek tek ya da elektromanyetik alanlar kullanılarak elektron plazmasından yakalanması ve özel teleskoplar aracılığıyla dış uzaydaki elektron plazmasının saptanması mümkündür. Elektronlar; elektronik, kaynak, katot ışını tüpleri, elektron mikroskopları, radyoterapi, lazerler, gaz iyonlaştırma sayaçları ve parçacık hızlandırıcıları gibi alanlarda kullanılırlar.
Atom çekirdeği içindeki pozitif yüklü protonlar ile dışındaki negatif yüklü elektronlar arasındaki Coulomb kuvveti etkileşimleri, atomları oluşturur. İyonlaşma ve parçacıkların özelliklerinde değişimler sistemin bağlanma enerjisini değiştirir. İki veya daha fazla atom arasında elektronların değişimi veya paylaşımı, kimyasal bağları meydana getirir. İlk olarak 1838 yılında Richard Laming tarafından atomların kimyasal özelliklerini açıklamak için elektron yükünün bölünemez bir özelliğinin olması kavramı hipotezleştirilmiştir. Johnstone Stoney 1891 yılında bu yüke elektron adını vermiş, J. J. Thomson ve ekibi ise 1897 yılında onu parçacık olarak tanımlamıştır. Beta parçacıkları olarak bilindikleri yıldız nükleosentezi gibi elektronlar nükleer reaksiyonlara katılırlar. Kozmik ışınların Dünya atmosferine girmeleri gibi yüksek enerjili çarpışmalarda ve radyoaktif izotopların beta bozunması yoluyla elektron oluşabilir. Pozitron olarak adlandırılan elektronun antiparçacığı, zıt simgeli elektrik ve diğer yükleri taşıması dışında elektronla aynıdır. Birer elektronla pozitron arasında yaşanan çarpışmada, her iki parçacık da gama ışını fotonları üreterek annihilasyona uğrayabilirler.
Tarihi
[değiştir | kaynağı değiştir]Elektrik kuvvetinin etkilerinin keşfi
[değiştir | kaynağı değiştir]Antik Yunanlar kehribarın, kürk ile sürtünmesi sonrasında küçük nesneleri çektiğini fark ettiler. Bu fenomen, şimşekle birlikte insanlığın elektrik hakkında kayıtlara geçmiş ilk deneyimiydi.[1] 1600'de yayımlanan De Magnete adlı eserinde William Gilbert, Latincede kehribar anlamına gelen ve Yunancada da aynı anlamı taşıyan ἤλεκτρον (elektron) electrum kelimesinden esinlenerek, sürtünme sonrası küçük nesneleri çekme özelliğini tanımlayan Yeni Latince electricus kelimesini türetti.[2][3] Thomas Browne'un 1646'da yayımlanan Pesudoxia Epidemica adlı eserinde, yine aynı kelimeler esas alınarak ilk defa İngilizcedeki electricity ifadesi kullanıldı.[2][3] Elektrik kelimesi Türkçeye, Fransızcada da aynı anlama gelen électrique kelimesinden geçti.[4]
İki tür yükün keşfi
[değiştir | kaynağı değiştir]1733'te yayımlanan Sur l'électricité adlı eserinde Charles François de Cisternay du Fay, yüklü altın varağın ipek sürtülen cam tarafından itildiğini, aynı yüklü altın varağın yün sürtülen kehribar tarafından ise çekildiğini gözlemlediğini yazdı. Buradan yola çıkarak du Fay, camsal ile kehribarsal adlarını verdiği iki tür elektrik akışı içerdiği sonucuna vardı. Bu iki akışkan, birleştirildiği vakit birbirini etkisiz hâle getiriyordu.[1][5] Bir müddet sonra Ebenezer Kinnersley de bağımsız olarak aynı sonucu elde etti.[6] 10 yıl sonra Benjamin Franklin, elektriğin iki farklı tür akıştan değil de fazla (+) ya da eksik (-) olacak şekilde aynı akıştan geldiğini tespit ederek bunlara, yüklerin modern gösterimi olan pozitif ve negatif isimlerini verdi.[7] Franklin, yükün taşıyıcısını pozitif olarak düşündü, ancak hangi durumda yük taşıyıcısının fazlası ve hangi durumda yük taşıyıcısının eksiği olduğunu tanımlayamadı.[8]
1838 ve 1852 yılları arasında Richard Laming; atomların, birim elektrik yüklerine sahip atomaltı parçacıklar tarafından çevrelenmiş maddenin özünün birleşimi olduğu fikrini ortaya attı.[9] Johnstone Stoney, elektroliz fenomenine dair çalışmalarının ardından 1874'te, "elektriğin tek kesin özelliği" olduğunu ve bunun da tek değerlikli iyonun yükü olduğunu öne sürdü. Faraday'in elektroliz kanunları aracılığıyla bu temel yükün (e) değerini tahmin edebilse de, bu yüklerin atomlara sabitlenmiş olduğuna ve ayrılamayacağına inanıyordu.[10] 1881'de Hermann von Helmholtz, hem pozitif hem negatif yüklerin "elektriğin atomları gibi davranan" temel parçalara ayrıldığı fikrini ortaya attı.[11] 1881'de Stoney, elektroliyon (electrolion) terimini bu temel yükleri adlandırmak için kullandı. 1894 tarihli yazısında: "...elektron (electron) adını önermeye teşebbüs ettiğim elektriğin bu en dikkat çekici, temel biriminin gerçek miktarının bir tahmini yapıldı" ifadeleriyle terimin adını değiştirdi. 1906 yılında önerilen elektriyon (electrion) kelimesi, Hendrik Lorentz'in elektron'u kullanmaya devam etmesi nedeniyle kabul görmedi.[12][13] Elektron kelimesi elektrik ve iyon kelimelerinin birleşimiyle oluşturulmuştu.[14] Günümüzde, atomaltı parçacıkları tanımlamak için kullanılan -on eki de elektron kelimesinden sonra kullanılmaya başlandı.[15][16]
Madde dışındaki serbest elektronların keşfi
[değiştir | kaynağı değiştir]
Seyreltilmiş gazlarda elektrik iletkenliği üzerine çalışmalarda bulunan Julius Plücker, 1859 yılında, katottan yayılan radyasyonun yol açtığı fosforesans ışığın, katodun yanındaki tüpte göründüğünü ve bu ışığın, manyetik alan uygulanmasına bağlı olarak hareket ettiğini gözlemledi.[17] 1869'da Johann Wilhelm Hittorf, katot ile tüpün duvarları arasında koyduğu katı bir cismin bir gölge oluşturduğunu tespit etti.[17] 1876'da Eugen Goldstein, bu cismin gölgesinin cisimden daha büyük boyutlarda olduğunu gözlemleyerek fosforesansı oluşturan ışınların katottan direkt bir yol izleyerek geldiğini belirledi ve bu ışınlara katot ışını (Almanca: Kathodenstrahlen) adını verdi.[17][18][19] 1869-1875 yılları arasında William Crookes, içerisine yüksek vakum olan bir tüp geliştirdi. 1874'te, katot ışınlarının izlediği yola koyulan bir çarkın, ışınların etkisiyle döndüğünü gözlemleyerek bu ışınların momentum taşıdığını ve katottan anoda doğru hareket ettiğini gösterdi.[20] Işınlara uyguladığı manyetik alanla ise ışınları saptırmayı başararak bu ışınların negatif yüklüymüş gibi davrandığını tespit etti.[19] 1879'da, "radyant madde" olarak tanımladığı şeyle bu özelliklerin açıklanabileceğini ve maddenin, negatif yükle yüklenmiş olan yüksek hızla katottan tasarlanmış moleküller dahil dört durumu olduğunu olduğunu ileri sürdü.[21]

Arthur Schuster, katot ışınlarına paralel iki metal levha yerleştirdi ve levhalar arasında bir elektrik potansiyeli uygulayarak Crookes'un deneyini ilerletti. Işınların, alanın etkisiyle pozitif yüklü levhaya doğru sapmasıyla negatif enerji taşıdığı kanıtlanmış oldu. 1890'da, akımın verilen seviyesi için sapma miktarını ölçerek ışın bileşenlerinin kütle-yük oranını tahmin etti. Ancak bu üretilen değer beklenenin bin katından fazlaydı, bu yüzden o dönemde kendisinin hesaplamaları yaygın bir biçimde kabul görmedi.[19] 1892'de Hendrik Lorentz, bu parçacıkların (elektronların) kütlelerinin, onların elektrik yükünün bir sonucu olabileceği fikrini ortaya attı.[22][23]
1896'da floresans mineraller üzerinde çalışmalar yürüttüğü sıralarda Henri Becquerel, bu minerallerin hiçbir dışsal enerji kaynağına maruz kalmadan radyasyon yaydıklarını keşfetti.[24] Sonrasında Ernest Rutherford, bu radyoaktif malzemelerin parçacık yaydığını tespit ederek bu parçacıkları maddeye nüfuz etme özelliklerine göre alfa ve beta olarak adlandırdı.[25] 1900'de Becquerel, radyumun yaydığı beta ışınlarının elektrik alanını saptırabileceğini ve kütle-yük oranlarının katot ışınlarındakinin aynısı olduğunu belirledi.[26] Bu bulgu, elektronların atomların bileşenleri olduğu fikri için bir kanıt oluşturuyordu.[27][28]
1897'de J. J. Thomson, John Townsend ve Harold Wilson, öncesinde düşünüldüğünün aksine katot ışınlarının dalga, atom veya molekülden farklı ve özgün parçacıklar olduğunu gösteren deneyler yaptı.[29] Thomson, katot ışın parçacıklarının bilinen en hafif iyon olan hidrojeninkinin binde biri olan kütlesinin (m) ve yükünün (e) doğru bir tahminini yaptı.[29] Yük-kütle oranının (e/m) katodun malzemesinden bağımsız olduğunu gösterdi. Devamında ise radyoaktif, sıcak veya aydınlatılmış malzemeler tarafından üretilen negatif yüklü parçacıkların evrensel olduğunu ispatladı.[29] Elektron ismi bir kez daha, Johnstone Stoney tarafından bu parçacıklar için önerildi ve ilerleyen dönemde evrensel olarak kabul gördü.[30]
1909'da gerçekleştirdikleri ve sonuçları 1911'de yayımlanan yağ damlası deneyi sonrasında Robert A. Millikan ve Harvey Fletcher, elektronların yüklerini daha hassas bir şekilde ölçtüler. Deneyde, yüklü yağ damlacığının yerçekimi yüzünden düşmesini önlemek için elektrik alanı kullandı. Bu araç sayesinde %0,3'ten az bir hata payıyla, 1-150 kadar az iyonun elektrik yükü ölçülebildi. Benzer deneyler de elektroliz tarafından yönetilen yüklü su damlacıkları bulutları kullanarak Thomson'ın ekibi tarafından daha önce yapılmıştı.[29] 1911'de ise Abram İoffe'nin, metallerin yüklü mikroparçacıklarını kullanarak yaptığı ve Milikan ile aynı sonuca bağımsız olarak ulaştığı deneylerin sonuçları 1913'te yayımlandı.[31]
20. yüzyılın başlarında, belirli koşullar altında hızlı hareket eden yüklü parçacığın yolu boyunca aşırı doymuş su buharı yoğunluğuna yol açtığı keşfedildi. 1911'de Charles Wilson'ın tasarladığı bulut odasında bu prensip kullanıldı ve böylelikle hızlı hareket eden elektronlar gibi yüklü parçacıkların izleri fotoğrafladı.[32]
Atom teorisi
[değiştir | kaynağı değiştir]
Ernest Rutherford, Henry Moseley, James Franck ve Gustav Hertz'in 1914'e kadar yaptıkları deneylerle, bir atomun yapısı düşük kütleli elektronla çevrili ve pozitif yüklerin yer aldığı yoğun bir çekirdeği olarak tanımladı.[33] 1913'te Niels Bohr, elektronların çekirdekle ilgili elektron yörüngelerinin açısal momentumlarıyla belirlenen enerjiyle beraber belli bir dereceye kadar enerji içeren durumlarda bulunduğunu tespit etti. Elektronlar, belli sıklıklardaki protonların yayılması veya emilmesi ile bu durumlar ve yörüngeler arasında hareket edebildiğini belirledi. Bu kuantumlanmış yörüngeler aracılığıyla, hidrojen atomunun bu spektrum çizgilerini açıkladı.[34] Fakat Bohr'un modeli bu spektrum çizgilerinin göreli yoğunluklarını hesaplamada yanıldı ve daha karmaşık atomların spektrumlarını açıklamakta başarılı olamadı.[33]
Atomların arasındaki kimyasal bağlar 1916 yılında, iki atom arasındaki kovalent bağın aralarında paylaştıkları elektron çiftleri tarafından korunduğunu ileri süren Gilbert Lewis tarafından açıklandı.[35] 1927'de, Walter Heitler ve Fritz London tarafından, elektron çiftlerinin oluşumu ile kimyasal bağların, kuantum mekaniği bağlamında tam açıklaması gerçekleştirildi.[36] 1919'da, Lewis'in statik atom modelini inceleyen Irving Langmuir, elektronların ardışık "konsentirik (neredeyse) küresel kabuklara dağılmış ve tamamının eşit kalınlıkta" olduğunu öne sürdü.[37] Kabukları, her biri birer elektron çifti içeren birkaç hücreye böldü. Bu modelle Langmuir, genellikle kendilerini periyodik kurallara göre tekrar eden periyodik tablodaki bütün elementlerin niteliksel olarak kimyasal özelliklerini açıklamayı başardı.[38]
1924'te Wolfgang Pauli, atomların kabuk benzeri yapılarının her durum birden fazla elektron tarafından belirlenmedikçe her kuantum enerji durumunu tanımlayan dört parametreyle açıklanabileceğini gözlemledi. Bu aynı kuantum enerji durumunu kaplayan birden fazla elektrona karşı yasaklama olayı, Pauli dışarlama ilkesi olarak kullanıma geçti.[39] İki farkı mümkün değere sahip dördüncü parametreyi açıklamak için kullanılan fiziksel mekanizma, 1925'te yörüngenin açısal momentumuna ek olan bir elektronun bir içsel açısal momentumu ve manyetik dipol momenti olduğunu belirten Samuel Goudsmit ve George Uhlenbeck tarafından belirlendi[33][40] Bu içsel açısal momentum, ilerleyen dönemlerde spin olarak adlandırıldı ve yüksek çözünürlüklü spektrografla gözlemlenen spektrum çizgilerinin daha önceleri nedeni bilinmeyen ve sonradan ince yapı bölünmesi olarak adlandırılan bir şekilde bölünmesini açıkladı.[41]
Kuantum mekaniği
[değiştir | kaynağı değiştir]
1924 tarihli Recherches sur la théorie des quanta adlı çalışmasında Louis de Broglie, bütün maddelerin ışık gibi bir dalgaya sahip olduğunu hipotezleştirdi.[42] Bulgulara göre uygun koşullar altındaki elektronlar ve diğer maddeler ya dalga ya da parçacık özellikleri gösteriyordu. Bir parçacığın parçacık özellikleri, verilen anda onun eğik hareketi boyunca uzayda yerleştirildiği konumu olduğu gösterilince ortaya çıkar.[43] 1927'de yaptıkları deneylerle George Thomson, metal bir folyodan bir elektron demetinin geçmesiyle; Clinton Davisson ile Lester Germer ise nikel kristalinden elektronların yansımasıyla elektronun girişim etkisini keşfetti.[44][45]
De Broglie'nin elektronların dalga yapısı öngörüsü sonrasında Erwin Schrödinger, atom çekirdeğinin etkisi altında hareket eden elektronlar için 1926'da oluşturduğu dalga denklemiyle elektron dalgalarının nasıl yayıldığını tanımladı.[46] Zamanla bu denklem, elektronun yerini belirleyen çözümü sağlamak yerine, özellikle elektron dalga denkleminin zamanla değişmediği uzayda bağlı elektronun olduğu bir pozisyona yakın bir elektron bulunması için de kullanıldı. Bu yaklaşım ikinci bir kuantum mekaniği formülasyonunun oluşturulmasına (ilki 1925'te Werner Heisenberg tarafından yapışmıştı) ve Heisenberg'inki gibi Schrödinger denkleminin çözümleri 1913'te Bohr tarafından elde edilenlere eşit olan ve hidrojen spektrumunu ürettiği bilinen hidrojen atomundaki bir elektronun enerji durumunun türevlerinin elde edilmesine yol açtı.[47] Spin ve çoklu elektronlar arasındaki etkileşimin tanımlanmasının ardından, kuantum mekaniği sayesinde hidrojenden daha yüksek atom numarasına sahip atomlardaki elektronların diziliminin öngörülmesi mümkün kılındı.[48]
1928'de Paul Dirac, Wolfgang Pauli'nin çalışmasını temel alarak görelilik teorisiyle uyumlu olan, kuantum mekaniğinin elektromanyetik alanının hamilton formülasyonuna göreli ve simetrik kavrayışları uygulayarak Dirac denklemi olarak adlandırılan bir elektron modeli oluşturdu.[49] Göreli denklemindeki bazı sorunları çözme amacıyla 1930'da, negatif enerjili parçacıklardan oluşan sonsuz bir deniz olan ve sonraları Dirac denizi olarak adlandırılan bir vakum modeli geliştirdi. Bu sayede elektronun benzer antimaddesi pozitronun varlığını öngördü.[50][51] Bu parçacık 1932'de, standart elektronlara negaton diyen ve elektron kelimesini pozitif ve negatif yüklü parçacıkları tanımlamak için kullanmayı öneren Carl Anderson tarafından keşfedildi.[52]
1947'de, Robert Retherford ile birlikte çalışan Willis Lamb, bir hidrojen atomunun aynı enerjiye sahip olması gereken belli kuantum durumlarında, sonraları Lamb kayması olarak adlandırılan farklılıklar yaşandığını buldu.[53] Henry Foley ile birlikte çalışmalarını yürüten Polykarp Kusch 1948'de, elektronun manyetik momentinin Dirac'ın teorisi tarafından öngörülenden daha büyük olduğunu buldu.[54] Anormal manyetik dipol moment olarak adlandırılan aradaki fark 1948'de Julian Schwinger tarafından açıklandı.[55]
Parçacık hızlandırıcılar
[değiştir | kaynağı değiştir]20. yüzyılın ilk yarısında parçacık hızlandırıcıların geliştirilmesiyle birlikte, atomaltı parçacıkların özellikleri üzerine yapılan araştırmalar da derinleşmeye başladı.[56] İlk elektromanyetik indüksiyon kullanarak elektronları hızlandırma denemesini 1940'ta gerçekleştiren Donald Kerst, yaptığı denemelerde betatronu ile 2,3 MeV enerjiye ulaşmayı başardı.[57] 1947'de, sinkrotron radyasyonu 70 MeV elektron sinkrotron ile General Electric'te keşfedildi. Bu radyasyon elektronların, manyetik alana doğru neredeyse ışık hızıyla hareket etmeleriyle meydana geldi.[58]
İlk yüksek enerji çarpıştırıcı, 1,5 GeV enerji demetiyle 1968'de hizmete giren ADONE'ydi.[59] Alet, elektronları ve pozitronları ters yönlerde, çarpışma enerjilerini bir elektronlu durağan bir hedefe çaptığındakinin iki katına çıkararak hızlandırıyordu.[60] 1989'dan 2000'e kadar etkin olan Avrupa Nükleer Araştırma Merkezindeki Büyük Elektron-Pozitron Çarpıştırıcısı, 204 GeV değerinde enerjiye ulaşan çarpışmalar gerçekleştirmeyi başardı.[61][62]
Özellikleri
[değiştir | kaynağı değiştir]Sınıflandırması
[değiştir | kaynağı değiştir]
Parçacık fiziğinin Standart Model'inde elektronlar, temel parçacıklar olduklarına inanılan lepton adlı atomaltı parçacık grubuna dahildirler. Elektronlar, yüklü herhangi bir leptondan ya da elektrik yüklenmiş herhangi bir tür parçacıktan daha düşük kütleye sahiptir ve temel parçacıkların ilk nesline aittir.[63] İkinci ve üçüncü nesillerdeki yüklü leptonlar olan müon ve tau; yük, spin ve etkileşim açısından elektronlar ile özdeş olsalar da daha büyük boyuttadırlar. Leptonlar, maddenin diğer basit bileşenlerinden olan kuarklardan, güçlü etkileşimi olmaması bakımından ayrılırlar. Lepton grubunun tüm üyeleri gibi elektronlar, yarım tam sayı spine (12) sahip olduklarından birer fermiyondur.[64]
Temel özellikleri
[değiştir | kaynağı değiştir]Elektronun durgun kütlesi 9,1093837015(28)×10-31 kilogram ya da 5,48579909065(16)×10-4 atomik kütle birimidir. Albert Einstein'ın kütle-enerji eşdeğerliği ilkesine göre bu kütle 0,51099895000(15) MeV durgun enerjiye tekabül eder. Protonun kütlesinin elektronunkine oranı yaklaşık 1836'dır.[65] Astronomik ölçümler bu oranın Standart Model'de öngörüldüğü gibi, en azından evrenin yaşının yarısından beri aynı kaldığını gösterir.[66]
Elektronlar, -1,602176634×10-19 coulomb kadar elektrik yüküne sahiptir.[65] Deneysel hassasiyet sınırları içinde elektronun yükü, protonunkinin aynısının zıt işaretlisidir.[67] Temel yük için e simgesinin kullanılması nedeniyle elektron, genellikle
e-
şeklinde, negatif yükü temsil eden eksi işaretiyle birlikte simgeler. Elektronla aynı özelliklere sahip olan ve elektronun aksine pozitif yüke sahip olan elektronun antiparçacığı pozitron ise
e+
şeklinde gösterilir.[64][65]
Elektronların, spin olarak adlandırılan içsel açısal momentumu 12'dir.[65] Bu spin değerine sahip parçacıklar için spin büyüklüğü ±ħ2 kadardır ve herhangi bir eksendeki spinin izdüşüm ölçümlerinin sonuçları yalnızca √32 ħ olabilir.[c] Spine ek olarak elektron, spin ekseni boyunca içsel bir manyetik momente sahiptir.[65] Bu değer yaklaşık olarak bir Bohr magnetonuna denk gelen 9,2847647043(28)×10-24 joule/tesla kadardır.[65][69][d] Elektronun momentumuna göre spinin yönünün belirlenmesi olayı, temel parçacıkların sarmallık olarak bilinen özelliğini ifade eder.[70]
Elektronun bilinen bir alt yapısı yoktur[71][72] ve uzamsal bir kapsamı olmayan, noktasal yüke sahip nokta parçacık olarak kabul edilir.[73] Klasik fizikte bir nesnenin açısal momentumu ve manyetik momenti, onun fiziksel boyutlarına bağlıdır. Elektronun boyutsuz olarak kabul edilmesinden dolayı, paradoksal ve elektronun sonlu ve sıfırdan farklı yarıçapına işaret eden Penning tuzağındaki deneysel gözlemlerle ters düşüyor gibi gözükebilir. Elektronun yarıçapı konusu, modern teorik fizikte birtakım sorunlara yol açar. Elektronun sonlu bir yarıçapı hipotezinin kabulü, görelilik teorisinin önermeleriyle uyumsuzdur. Diğer yandan, nokta benzeri elektron (sıfır yarıçaplı) sonsuzluğa yönelen elektronun öz enerjisi nedeniyle matematiksel zorlulara yok açar. Bir Penning tuzağındaki tek bir elektronda, parçacığın yarıçapının üst sınırının 10−22 metre olduğunu gözlemlenmiştir.[74] Enerjideki belirsizlik ilkesi kullanılarak üst sınırın 10−18 metre olduğu da söylenebilir.[75] Protonun yarıçapından fazla, klasik elektron yarıçapı denilen çok daha fazla değeri olan 2,8179×10-15 m kadar, "klasik elektron yarıçapı" adı verilen bir fiziksel sabit daha olmakla birlikte bu değer, kuantum mekaniğinin etkilerini göz ardı eden basitleştirilmiş bir hesaplama ile elde edildiğinden dolayı elektronun yapısıyla ilgili gerçeği yansıtmaz.[76][e]
Elektron, bazı temel parçacıkların aksine teorik temellerde kararlıdırlar ve daha küçük boyutlu parçacıklara bozunmazlar. Sıfırdan farklı elektrik yüküne sahip parçacıklar arasında en düşük boyuta sahip olan elektronların bozunması, yük korunumunu ihlal etmesi anlamına gelecektir.[78] Elektronun deneysel ortalama yaşam süresi için alt sınır, %90 güvenilirlikle 6,6×1028 yıldır.[79][80][81]
Kuantum özellikleri
[değiştir | kaynağı değiştir]
Tüm parçacıklar gibi elektronlar da dalga gibi davranabilirler. Buna dalga-parçacık ikiliği denir ve çift yarık deneyi kullanarak gösterilebilir.[82] Elektronun dalga benzeri yapısı klasik parçacıklardaki gibi tek yarık yerine, paralel yarıklarından aynı anda geçmesine izin verir. Kuantum mekaniğinde bir parçacığın dalga benzeri özelliği genellikle ψ simgesiyle gösterilir ve karmaşık değerli dalga fonksiyonu ile matematiksel olarak tanımlanabilir. Bu fonksiyonun mutlak değerinin karesi alındığında, bir parçacığın bir konumunun yakınında gözlemlenme (olasılık yoğunluğu) ihtimalini verir.[83]

Elektronlar, içsel özelliklerine bakılarak birbirlerinde ayrılamadıkları için özdeş parçacıklardır. Kuantum mekaniğinde bu, etkileşen bir çift elektronun konumlarının, sistemin durumunda gözlemlenebilir hiçbir değişiklik olmadan değiştirilebileceği anlamı taşır. Elektronlar dahil fermiyonların dalga fonksiyonu antisimetriktir. Bu sayede iki elektron, r1 ve r2 sırasıyla birinci ve ikinci elektronları ifade edecek biçimde, ψ(r1, r2) = -ψ(r2, r1) denklemine göre yer değiştirdiğinde elektronların işaretleri de değişir. Simge değişiminde mutlak değerlerde değişim yaşanmadığından olasılıklar eşittir.[83] Antisimetri durumunda, elektronların etkileşimi için dalga denkleminin çözümleri bir çiftin aynı yeri veya durumunu kapsaması sıfır olasılıkla sonuçlanır. Bir atomdaki bağlı elektron gruplarının aynı yörüngede birbirleriyle çakışması yerine farklı yörüngelerde bulunması, iki elektronun aynı kuantum durumunda olmasını engelleyen Pauli dışlama ilkesiyle açıklanabilir.[83]
Sanal parçacıklar
[değiştir | kaynağı değiştir]
Her foton, sonrasında hızlıca annihilasyona uğrayan sanal elektron ile antiparçacığı sanal pozitronu birlikte barındıracak şekilde bir süreliğine var olur.[84] Enerji çeşitliliğinin birleşiminin bu parçacıkları üretmesi ve var oldukları süre boyunca, ΔE · Δt ≥ ħ formülüyle belirsizlik ilkesinde açıklanan keşfedilebilirlik eşiğine dahil olması gerekse de gerçekte, bu sanal parçacıkların üretimi için gerekli enerji olan ΔE, Δt boyunca vakumdan "ödünç" alınır ve bu sayede ürünleri indirgenmiş Planck sabitinden (ħ ≈ 6,6×10-16 eV·s) daha büyük olamaz. Bu durumda sanal bir elektron için Δt değeri en fazla 1,3×10-21 s olabilir.[85]
Sanal bir elektron-pozitron çifti varken, bir elektronu çevreleyen elektrik alanından gelen Coulomb kuvveti, özgün elektronun oluşturulan pozitronu çekmesine, oluşturulan elektronu ise itmesine yol açar. Bu sayede vakum kutuplaşması olarak adlandırılan olay meydana gelir. Gerçekte vakum, bir birimden fazla dielektrik geçirgenliğine sahip bir ortam gibi davranır. Böylece, etkin değeri, gerçek değerinden düşük olan elektronun yükü, kendisinden uzaklaştıkça düşer.[86][87] Bu kutuplaşma, TRISTAN parçacık hızlandırıcısı kullanılarak 1997 yılında deneysel olarak kanıtlanmıştır.[88] Sanal parçacıklar elektronun kütlesi için benzer bir perdeleme etkisi oluştururlar.[89]
Sanal parçacıklarla etkileşim, elektronun içsel manyetik momentumunun Bohr magnetonundan %0,1 kadar sapmasını da açıklar.[69][90] Noktasal bir parçacık olan elektronun içsel açısal momentuma ve manyetik momente sahip olması nedeniyle klasik fizik paradoksu, elektron tarafından üretilen elektrik alanındaki sanal fotonların oluşturulmasıyla açıklanabilir. Bu fotonlar, titreşim hareketi olarak adlandırılan elektronların yer değiştirmesi olayına neden olur.[91] Bu hareket, elektronun hem spinini hem de manyetik momentumunu üretir.[73][92] Atomlarda bu sanal parça üretimi, spektrum çizgilerinde gözlenen Lamb kaymasını da açıklar.[86]
Etkileşim
[değiştir | kaynağı değiştir]Bir elektronun ürettiği elektrik alanı, pozitif yüklü parçacıklara çekme, negatif yüklü parçacıklara ise itme kuvveti uygular. Bu kuvvetin gücünün büyüklüğü Coulomb kanunuyla saptanır.[93] Elektronlar, hareket hâlindeyken manyetik alan oluştururlar.[83] Manyetik alan ile elektronların kütle hareketleri (akım) arasındaki ilişki Ampère kanunu ile açıklanır. İndüksiyonun bu özelliği, bir elektrik motorunu harekete geçiren manyetik alanı sağlar.[94] Rastgele hareket eden yüklü bir parçacığın elektromanyetik alanı, parçacığın hızı ışığınkine (göreli) yakın olduğunda dahi geçerli olan Liénard-Wiechert potansiyelleriyle açıklanır.[95]

Manyetik bir alana doğru hareket eden bir elektron, hızı ile manyetik alana bağlı olan ve düzleme dik etki eden Lorentz kuvvetine maruz kalır. Bu merkezcil kuvvet nedeniyle elektron, eylemsizlik yarıçapı denilen bir yarıçapa sahip alana doğru sarmal bir yörünge izler. Bu eğimli hareketin ivmesi elektronun sinkrotron radyasyonu biçiminde enerji yaymasına yol açar.[96][97][f] Elektronun alanının, kendisi üzerindeki karşı tepkiden kaynaklanan Abraham-Lorentz-Dirac kuvveti olarak bilinen sürtünme kuvveti ise, elektronu yavaşlatır.[98]

Fotonlar, parçacıklar arasındaki etkileşimi sağlarlar. Sabit bir hızda izole edilmiş bir elektronun, enerji ve momentumun korunumu kanunlarını ihlal etmiş olacağından gerçek bir fotonu emmesi ya da yayması mümkün değildir. Bunun yerine sanal fotonlar, iki yüklü parçacık arasında momentum aktarımı yapabilirler. Sanal fotonların bu değişimi Coulomb kuvvetini üretir.[99] Hareket eden bir elektronun, proton gibi yüklü bir parçacık tarafından saptırılmasıyla enerji salınımı gerçekleşebilir. Elektronun ivmelenmesi, Bremsstrahlung radyasyonunun salınımı ile sonuçlanır.[100]
Bir foton ile serbest bir elektron arasında yaşanan esnek olmayan çarpışmaya Compton saçılması denir. Bu çarpışma ile parçacıklar arasında momentum ve enerji aktarımı yaşanarak fotonun dalga boyu, Compton kayması olarak adlandırılan miktar kadar değişir.[g] Bu dalga boyu değişiminin en büyük değeri, Compton dalga boyu olarak bilenen h/mec formülüyle tanımlanır ve elektronlar için bu değer yaklaşık 2,43×10-12 m kadardır.[65] Işığın dalga boyu uzadıkça (örneğin görülebilen ışığın dalga boyu 0,4-0,7 μm'dir) dalga boyu kayması daha ihmal edilebilir hâle gelir. Işık ile serbest elektronlar arasındaki bu ilişki, Thomson saçılması olarak adlandırılır.[102]
Elektron ve proton gibi iki yüklü parçacık arasındaki elektromanyetik etkileşimin göreli gücü, ince yapı sabiti ile verilir. Bu değer, bir Compton dalga boyunun ayrımındaki çekmenin ya da itmenin elektrostatik enerjisinin, yükün geri kalan enerjisine oranı ile elde edilen boyutsuz bir niceliktir. α ≈ 7,297353×10-3 şeklindeki bu değer yaklaşık olarak 1137'e eşittir.[65]
Elektronlar ile pozitronlar çarpıştığında, toplam enerjisi 1,022 MeV olan iki ya da daha fazla gama ışını fotonu ortaya çıkararak birbirlerini yok ederler. Elektron ve pozitronun ihmal edilebilecek derecede bir momentuma sahip olmaları durumunda, annihilasyon tamamlanmadan önce bir pozitronyum atomu da oluşabilir.[103][104] Diğer yandan yüksek enerji bir foton, çift üretimi denilen süreç sonrasında, yalnızca bir atom çekirdeği gibi yakındaki bir yüklü parçacığın varlığında birer elektron ve pozitrona dönüşebilir.[105][106]
Elektrozayıf etkileşim teorisine göre, elektronun dalga fonksiyonun sola dönen bileşeni ile elektron nötrino bir zayıf izospin çifti meydana getirir ve bu, zayıf etkileşimler süresince elektron nötrinolarının elektron gibi davrandıkları anlamına gelir. Bu çiftin herhangi bir üyesi, bir W bozonu yayarak ya da emerek bir yüklü akım etkileşimine maruz kalabilir ve çiftin diğer üyesine dönüşebilir. Bir yük taşıyan W bozonunun dönüşüm sırasında net yükü sıfırlaması nedeniyle bu reaksiyon boyunca yük korunur. Yüklü akım etkileşimleri, radyoaktif bir atomdaki beta bozunmasından sorumludur. Hem elektron ve hem de elektron nötrinosu,
Z0
değişimi sayesinde nötr akım etkileşimine maruz kalmakta ve bu sayede nötrino-elektron esnek saçılması ortaya çıkar.[107]
Atom ve moleküller
[değiştir | kaynağı değiştir]
Elektronlar, çekici Coulomb kuvvetiyle bir atomun çekirdeğine bağlanabilirler. Bir çekirdeğe bağlı bir ya da daha fazla elektronun oluşturduğu sisteme atom, elektron sayısının, atom çekirdeğinin elektrik yükünden farklı olduğu atomlara ise iyon denir. Bağlı elektronun dalga benzeri davranışları, atomik orbital işleviyle açıklanır. Her orbitalin kendisine ait enerji, açısal momentum ve açısal momentumun izdüşümü gibi kuantum sayıları vardır ve sadece bu orbitallerin ayrık grupları çekirdeğin etrafında var olabilir. Pauli dışarlama ilkesine göre her bir orbital, spin kuantum sayısı farklı olan en fazla iki elektron içerebilir.[108]
Elektronlar, potansiyel farkıyla aynı enerjili fotonların salınması ya da emilmesiyle farklı orbitallere aktarılabilirler.[109] Elektronlar gibi parçacıklarla çarpışmalar ve Auger etkisi ile de aktarım gerçekleşebilir.[110] Bir elektronun atomdan ayrılması için, kendisini atoma bağlayan bağ enerjisinin üstünde bir enerji gerekir. Bu durum, atomun iyonlaşma enerjisini aşan bir uyarıcı fotonun elektron tarafından emildiği fotoelektrik etkisiyle oluşabilir.[111]
Elektronların orbital açısal momentumu kuantumlanmıştır. Yüklü bir parçacık olmasından dolayı elektron, açısal momentumlaa orantılı bir orbital manyetik momentum da meydana getirir. Atomun net manyetik momenti, çekirdek ile tüm elektronların spin manyetik momentlerinin vektörel toplamına eşittir. Çekirdeğin manyetik momenti, elektronlarınkine kıyasla ihmal edilebilir düzeydedir. Aynı orbitalde yer alan elektronların (çiftlenmiş elektronlar denir) manyetik momentleri birbirlerini yok eder.[112]
Atomlar arasındaki kimyasal bağ, kuantum mekaniği kanunlarıyla tanımlanan elektromanyetik etkileşimlerin sonucunda ortaya çıkar.[113] Atomlar arasında elektron paylaşımı ya da aktarımıyla meydana gelen en güçlü bağlar, molekülleri oluşturur.[114] Bir moleküldeki birkaç çekirdeğin etkisinde hareket eden elektronlar, moleküler orbitallerin yanı sıra, izole atomların atomik orbitallerinde yer alırlar.[115] Bu moleküler yapılardaki temel etmen, elektron çiftlerinin varlığıdır. Bu elektronlar, zıt spinli olduklarından Pauli dışarlama ilkesini ihlal etmeden aynı moleküler orbitalde bulunabilirler. Moleküler orbitallerdeki elektron yoğunlukları, farklı uzamsal dağılımlarına sahiptir. Örneğin, atomları bir araya bağlayan çiftler gibi bağlı çiftlerdeki elektronlar, çekirdeklerin arasındaki görece küçük hacimli bölgede daha yüksek yoğunlukta bulunur. Tam aksine, bağlı olmayan elektron çiftleri, çekirdeğin etrafındaki görece büyük hacimli bölgeye dağılmıştır.[116]
İletkenlik
[değiştir | kaynağı değiştir]
Bir yapının çekirdeklerindeki proton sayısı elektron sayısından fazlaysa yapı pozitif, tersi durumda ise negatif yüklüdür. Elektron ve protonların sayısı aynı ise yükleri birbirlerini sıfırlar ve yapı, elektriksel olarak nötr olur. Makroskobik yapılar sürtünme ile elektriklenebilirler.[120]
Vakumda hareket eden bağımsız elektronlar, serbest elektron olarak tanımlanır. Metallerdeki elektronlar da serbestlermiş gibi davranır. Gerçekte ise metal ve diğer katılardaki elektron olarak adlandırılan parçacıklara sanki elektron denir ve gerçek elektronlar ile aynı elektrik yükü, spin ve manyetik momente sahip olsa da kütle açısından farklılık gösterebilirler.[121] Hem metal hem de vakumdaki serbest elektronlar hareket ettiklerinde, manyetik alan üreten ve elektrik akımı olarak adlandırılan net bir yük akışı oluştururlar. Manyetik alan değişimi ile de elektrik akımı yaratılabilir. Bu etkileşimler, matematiksel olarak Maxwell denklemleriyle tanımlanırlar.[122]
Belirli bir sıcaklıkta her malzeme, elektrik potansiyelinin uygulandığında meydana gelen elektrik akımının değerini belirleyen bir elektrik iletkenliğine sahiptir. Dielektrik malzemelerde elektronlar kendi atomlarına bağlı kalırken malzemeler de bir yalıtkan gibi davranır. Çoğu yarı iletken malzeme, yalıtmanın ve iletmenin sınırları arasında olan farklı iletkenlik seviyesine sahiptir.[123] Diğer yandan metaller, kısmen dolu elektronik bantlardan oluşan bir yapıya sahiptir. Bu bantların varlığı, metallerdeki elektronların serbest veya yöresizleşmiş elektronlarmış gibi davranmalarına yol açar. Bu elektronlar belli atomlarla ilişkilendirilmemiş olduklarından, bir elektrik alanı uygulandığında, serbest elektronlara benzer şekilde malzemeye doğru gaz gibi (Fermi gazı denir) gibi hareket etmekte serbesttir.[124]
Elektronlar ile atomlar arasındaki çarpışmalardan dolayı bir iletkendeki elektronların sürüklenme hızı saniyede milimetreler bazındadır. Malzemenin bir noktasındaki akımın değişmesi ile diğer bölümlerindeki akımların da değişmesine neden olan hız faktörü, ışık hızının %75'i kadardır.[125] Bu durum elektrik sinyallerinin, malzemenin dielektrik sabitine bağımlı bir hızla dalga gibi yayılması nedeniyle gerçekleşir.[126]
Hareket alanı genişleyen elektronların atomlar arasındaki ısı enerjisini taşımak için serbest bir şekilde hareket etmelerinden dolayı metaller, görece ısıyı iyi iletirler. Metallerin ısı iletkenlikleri, elektrik iletkenliklerinin aksine sıcaklıktan neredeyse bağımsızdır. Bu durum matematiksel olarak, ısı iletkenliğinin elektrik iletkenliğine oranının sıcaklıkla orantılı olduğunu söyleyen Wiedemann-Franz kanunuyla açıklanır.[124] Metalik kafesteki ısı düzensizliği, elektrik akımına bağımlı sıcaklık üreterek metalin elektrik direncini artırır.[127]
Malzemeler, kritik sıcaklık denilen noktanın altındaki bir noktaya kadar soğutulunca, elektrik akımına karşı tüm dirençlerini kaybettikleri süperiletkenlik olarak adlandırılan faz değişimine uğradıkları bir sürece girerler. BCS teorisinde, Cooper çifti olarak adlandırılan elektron çiftleri, fonon olarak adlandırılan örgü titreşimleriyle yakınlarında bulunan maddeyle hareketlerini eşleştirerek normalde elektrik direnci oluşturan atomlarla çarpışmaktan kaçınırlar (Cooper çiftlerinin yarıçapı 100 nm kadar olduğundan birbirleriyle üst üste binmeleri mümkündür).[128]
İletken katıların içindeki elektronlar, sözde parçacıktır ve mutlak sıfıra yakın sıcaklıklarda sıkıca hapsedildiklerinde; spinon, orbiton ve holonlar olmak üzere üç farklı sanki parçacığa bölünmüş gibi davranırlar. Spinonlar spin ve manyetik moment, orbitonlar orbital konum, holonlar ise elektrik yükü taşırlar.[129][130]
Hareket ve enerji
[değiştir | kaynağı değiştir]
Özel görelilik teorisine göre, bir elektronun hızı ışık hızına yaklaştıkça gözlemcinin bakış açısına göre bağıl kütlesi artar. Böylelikle gözlemcinin konuşlanma sistemine göre elektronu hızlandırmak gittikçe zorlaşır. Elektronun hızı, vakumdaki ışık hızına (c) yaklaşabilir ancak hiçbir zaman ulaşamaz. Göreli (c'ye yakın bir hızda hareket eden) elektronlar, su gibi, ışık hızının c'den ihmal edilemeyecek kadar az olduğu dielektrik bir ortama sokulduklarında geçici olarak ortamdaki ışıktan daha hızlı hareket ederler. Ortamla etkileşime girdiklerinde ise Çerenkov radyasyonu olarak bilinen zayıf bir ışık oluştururlar.[131][132]
Özel göreliliğin etkileri, Lorentz faktörü olarak bilinen ve şeklinde tanımlanan bir niceliğe bağlıdır. Buradaki v, parçacığın hızını ifade eder. Bu hızla hareket eden elektronun kinetik enerjisi Ke ise şu şekildedir:
Buradaki me, elektronun kütlesidir. Örneğin, SLAC Ulusal Hızlandırıcı Laboratuvarı bir elektronu yaklaşık 51 GeV'e kadar hızlandırabilir.[133] Verilen hızda elektron dalga gibi davrandığı için de Broglie dalga boyu karakterine sahiptir. Bu değer, λe = h/p denklemiyle elde edilir (h Planck sabitini, p momentumu ifade eder).[134] Yukarıdaki 51 GeV değerine sahip elektron dalga boyu, atom çekirdeğinden küçük yapıları keşfetmeye yetecek kadar düşük olan 2,4×10-17 m'dir.[135]
Oluşumu
[değiştir | kaynağı değiştir]
γ
) yol açtığı birer elektron (
e-
) ve pozitron (
e+
) çifti üretimi. Çizimdeki şimşek simgesi, sanal bir fotonun değişimini temsil eder.
Büyük Patlama teorisine göre patlamanın ilk milisaniyesinde, sıcaklık 10 milyar Kelvin'in üzerindeydi ve fotonların ortalama enerjisi bir milyon elektronvolttan yüksekti. Bu fotonlar elektron ve pozitron çiftleri kurmak için birbirleriyle etkileşime girmeye yetecek kadar enerjiye sahipti. Aynı şekilde, pozitron-elektron çiftleri birbirlerini annihilasyona uğratarak enerjili fotonlar yaydı:
Elektron, proton ve fotonlar arasındaki bu denge, evrenin evriminin bu safhası boyunca devam etti. 15 saniye geçmesinin ardından evrenin sıcaklığı, elektron-pozitron yapısının ortaya çıkma eşiğinin altına düştü. Kalan elektron ve pozitronların çoğu, evreni tekrar ısıtan gama radyasyonu salınımı yaparak birbirlerini annihilasyona uğrattılar.[136]
Annihilasyon süreci boyunca, bilinmeyen nedenlerden ötürü parçacık sayısı antiparçacığınkinden fazla olmasından ötürü her bir milyar elektron-pozitron çiftinden bir kadar elektron arta kaldı. Bu durum, antiprotonlar yerine fazla protonların eşleşmelerine ve baryon asimetrisi olarak adlandırılan durumun ortaya çıkmasıyla evrendeki net yükün sıfır olmasına yol açtı.[137][138] Kalan proton ve nötronlar, nükleosentez olarak bilinen süreçle, hidrojen ve helyum izotopları ile eser miktarda lityum oluşturacak biçimde birbirleriyle reaksiyonlara girmeye başladılar. Bu süreç, yaklaşık 5 dakikanın ardından zirve yaptı.[139] Kalan nötronlar, yaklaşık bin saniyelik yarı ömürlerinin ardından negatif beta bozunmasına maruz kalarak birer proton ve elektron yaydı:
Sonraki 300.000-400.000 yıllık süreçte arta kalan elektronlar, atom çekirdeğiyle bağ kurmak için fazla enerjiye sahipti.[140] Yeniden birleşme olarak adlandırılan sonraki safhada, nötr atomlar oluştu ve genişleyen evren, radyasyona uğrayabilecek derecede saydamlaştı.[141]
Büyük Patlama'dan kabaca bir milyon yıl sonra yıldızların birinci nesli oluşmaya başladı.[141] Yıldızlarda gerçekleşen nükleosentez, atom çekirdeğinin füzyonu sonrasında, elektronlarla annihilasyona uğrayarak gama ışınları salan pozitronların oluşumuna yol açar. Süreç, elektron sayısında sabit bir düşüş ve nötron sayısında bununla eşdeğer bir artışla sonuçlanır. Bununla birlikte yıldız evrimi süreci, radyoaktif izotopların senteziyle de yaşanabilir. Seçilmiş izotoplar, beta bozunmasına maruz kalarak atom çekirdeğinden birer elektron ve antinötrino salınımı yapabilirler.[142] Bozunarak nikel-60 (60Ni) oluşturan kobalt-60 (60Co) izotopu, bu duruma örnektir.[143]
Güneş'inkinden yaklaşık 20 kat büyük kütleli yıldızlar, yaşam süresinin sonunda kütleçekimsel çökmeye uğrayarak kara delik oluşturabilirler.[144] Klasik fiziğe göre bu nesneler, elektromanyetik radyasyon dahil, Schwarzschild yarıçapından kaçınacak herhangi bir şeyi engelleyecek kadar güçlü bir kütleçekimsel çekime sahiptirler. Ancak kuantum mekaniği etkilerinin potansiyel olarak bu mesafeden Hawking radyasyonunun yayılımına izin verdiği tahmin edilir. Elektron ve pozitronların, bu yıldız kalıntılarının olay ufkunda meydana geldiği düşünülür.[145]
Sanal bir parçacık çifti (örneğin elektron-pozitron çifti) olay ufku civarında oluştuğunda rastgele uzamsal dağılımı, bu parçacıklardan birinin dışarıda görünmesine izin verir. Bu süreç, kuantum tünelleme olarak adlandırılır. Kara deliğin kütleçekimsel potansiyeli, bu sanal parçacığın gerçek parçacığa dönüşmesi için gereken enerjiyi sağlayabilir.[146] Buna karşılık çiftin diğer üyesine kara delik tarafından, kütle enerjisinde net bir kayba yol açan negatif enerji verilir. Hawking radyasyonunun oranı, kütlenin azalmasıyla artar ve bu artış, kara deliğin patlayıncaya kadar buharlaşmasına yol açar.[147]
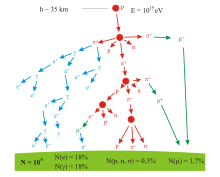
Kozmik ışınlar, yüksek enerjiyle uzayda hareket eden parçacıklardır ve bunlardaki en yüksek enerji değeri 3,0×1020 eV olarak kaydedilmiştir.[148] Bu parçacıklar Dünya atmosferinde nükleonlarla çarpışınca, pionların da yer aldığı bir parçacık sağanağına neden olur.[149] Dünya'nın yüzeyinden gözlemlenen kozmik radyasyonun yarısından fazlası, mezosferdeki pionların bozunması sonucu oluşan leptonlar olan müonları içerir:
Müonlar da elektron ya da pozitron oluşturacak şekilde bozunabilirler:[150]
Gözlemlenmesi
[değiştir | kaynağı değiştir]
Elektronların uzaktan gözlemlenmesi için radyasyon yapan enerjilerinin saptanması gerekir. Örneğin, bir yıldızın taç küresi gibi yüksek enerjili ortamlardaki serbest elektronlar, Bremsstrahlung radyasyonu nedeniyle enerji saçan bir plazma oluşturur. Elektron gazı, elektron yoğunluğundaki eşzamanlı değişimlerin yol açtığı dalgalar olan plazma salınımına maruz kalır ve radyo teleskoplar kullanarak tespit edilebilen bir enerji yayılımı üretir.[152]
Fotonların frekansları, enerjileriyle oranlıdır. Bir atomun enerji seviyelerinde geçiş yapan bağlı elektronlar, karakteristik frekanslardaki protonları emer ya da yayar. Örneğin atomlar, bir geniş spektrum kaynağı tarafından radyasyona maruz bırakıldığında, iletilen radyasyonun spektrumunda ayrı soğurma çizgileri görünür. Her element ya da molekül, hidrojen spektrumu serileri gibi karakteristik spektral çizgi grubuna sahiptir. Bu çizgilerin kuvvet ve genişliklerinin spektroskopik ölçümleri, maddenin fiziksel özelliklerinin ve bileşenlerinin tespitini sağlar.[153][154]
Laboratuvar koşullarında bireysel elektronlar arasındaki etkileşimler; enerji, spin ve yük gibi belirli özelliklerin ölçümüne olanak sağlayan parçacık dedektörleriyle yapılabilir.[111] Paul ve Penning tuzaklarının geliştirilmesiyle birlikte yüklü parçacıkların daha uzun süreler boyunca küçük bir alanda tutulabilmeleri mümkün hâle geldiğinden parçacık özelliklerinin daha net ölçülebilmeye başlanmıştır. Elektronun manyetik momenti 1980'de, diğer bütün fiziksel sabitlerden daha kesin olarak 11. basamağa kadar bir hassasiyetle ölçülebilmiştir.[155]
Elektronun enerji dağılımının ilk video görüntüleri Şubat 2008'de, Lund Üniversitesindeki bir ekip tarafından kaydedildi. Deneylerde, attosaniye darbeleri olarak adlandırılan ışık parlamaları kullanılarak elektronun hareketi ilk kez gözlemlenebilmişti.[156]
Katı malzemelerdeki elektron dağılımı, açı çözümlemeli fotoemisyon spektroskopisi tarafından görselleştirilebilir. Fotoelektrik etkisini, özgün yapıyı anlayabilmek için kullanılan periyodik yapıların matematiksel bir gösterimi olan ters uzayı ölçmek için kullanan bu teknik; malzemedeki elektronların yön, hız ve dağılımlarını belirlemek için kullanılabilir.[157]
Plazma uygulamaları
[değiştir | kaynağı değiştir]Parçacık demetleri
[değiştir | kaynağı değiştir]
Elektron demetleri, kaynakta kullanılır.[159] 0,1-1,3 mm arasındaki odak çapı boyunca, 107 W·cm-2'ye kadarki enerji yoğunluklarında elektron demetleriyle kaynak yapılabilir ve genellikle dolgu malzemesi gerektirmezler. Normalde kaynak için uygun olmayan iletken malzemeleri birleştirmek için kullanılan bu teknik, elektronların hedefe ulaşmalarından önce gazla etkileşmemesi amacıyla vakumda gerçekleştirilir.[160][161]
Elektron demeti litografi, mikrometreden daha küçük çözünürlüklerdeki yarı iletkenleri aşındırma yöntemidir.[162] Görece yüksek maliyetli olması, yavaş çalışması, ışınların vakumda çalışması gerekmesi, elektronların katılardaki dağılma eğilimi olması ve 10 nm'ye kadar çözünürlük sınırı olması nedeniyle, özelleştirilmiş entegre devrelerin üretiminde kullanılır.[163]
Elektron ışınıyla işleme, fiziksel özelliklerini değiştirmek ya da tıp ve gıda ürünlerini sterilize etme amacıyla metalleri radyasyona uğratmak için kullanılır.[164] Elektron demetleri, yoğun radyasyonda sıcaklık artışına sebep olmadan camları akışkanlaştırır ya da sözde erimesini sağlar. Örneğin yoğun elektron radyasyonu, viskozite şiddetinin ani, aktivasyon enerjisinin ise aşamalı olarak düşmesine sebep olur.[165]
Doğrusal parçacık hızlandırıcılar, elektron demetlerini üreterek tümörlerin radyoterapi yöntemiyle tedavisinde kullanılır. Elektron demetleri soğrulmadan önce belli bir sınırdaki derinliğe (5-20 MeV aralığında enerjiye sahip elektronlar için genelde 5 cm'ye kadar) kadar etki edebilmelerinden dolayı elektroterapi, bazal hücreli karsinom gibi yüzeysel deri bozukluklarının tedavilerinde de etkilidir. Elektron demetleri ayrıca, X ışınları tarafından radyasyona maruz kalmış bölgelerin tedavisinde destekleyici olarak da kullanılır.[166][167]
Parçacık hızlandırıcılar, elektrik alanları kullanarak elektron ve antiparçacıkların enerjilerini yükseltir. Bu parçacıklar, manyetik alanlardan geçerken sinkrotron radyasyonu yayarlar. Bu radyasyonun yoğunluğunun spine bağlı olmasının elektron demetini kutuplaştırmasına Sokolov-Ternov etkisi denir. Kutuplanmış elektron demetleri, çeşitli deneylerde kullanılır. Sinkrotron radyasyonu ayrıca, elektron demetlerinin soğutularak parçacıkların momentum yayılımlarının azaltılmasını sağlar. Elektron ve pozitron demetleri, ortaya çıkan enerjinin parçacık dedektörleriyle gözlemlenmesi için, gerekli enerjiye ulaşana kadar hızlandırılarak çarpıştırılırlar.[168]
Görüntüleme
[değiştir | kaynağı değiştir]
Düşük enerjili elektron kırınımı, kristal malzemeleri koşutlanmış elektron demeti bombardımanına tutma ve sonrasında ortaya çıkan kırınım desenlerini gözlemleyerek malzemenin yapısını belirlemek için kullanılan bir yöntemidir. Elektronların sahip olmaları gereken enerji genellikle 20-200 eV arasındadır.[169] Yansımalı yüksek enerjili elektron kırınımı ise çeşitli dar açılardan yollanan elektron demetini kullanarak kristal malzemelerin yüzeyini belirleme yöntemidir. Demet enerjisi genellikle 8-20 keV, geliş açısı ise 1-4° aralığındadır.[170][171]
Elektron mikroskobu, gözlemlenmek istenen numuneye, odaklanmış elektron demeti gönderir. Bazı elektronlar, demetin malzeme ile etkileşime girmesiyle birlikte malzemenin hareket yönü, açısı ve bağıl fazı ve enerjisi gibi özelliklerini değiştirirler. Gözlemciler, elektron demetindeki bu değişimleri kaydederek malzemenin kararlı atomik görünüşünü elde ederler.[172] Mavi ışıkta, geleneksel optik mikroskoplar yaklaşık 200 nm'lik kırınımla sınırlı çözünürlüğe sahiplerdir.[173] Elektron mikroskopları ise elektronun de Broglie dalga boyu ile sınırlılardır. Örneğin 100.000 volt değerindeki potansiyel boyunca hızlandırılan elektronlar için dalga boyu 0,0037 nm'dir.[174] Transmission Electron Aberration-Corrected Microscope, bireysel atomları çözümlemek için yeterli olan 0,05 nm'nin altında çözünürlük kapasitesine sahiptir.[175]
Geçirimli ve taramalı olmak üzere iki tür elektron mikroskobu vardır. Geçirimli elektron mikroskopları, bir malzeme parçasından geçen elektron demetiyle bu malzemenin yük bağlaşımlı aygıta ya da fotoğraf slayda lenslerle yansıtılmasını sağlayarak tepegöz gibi çalışırlar. Taramalı elektron mikroskopları ise televizyonda olduğu gibi çalışılmış örnekten görüntü üretmek için iyi odaklanmış elektrona raster tarama yaparlar. Magnifikasyon oranı her iki mikroskop türünde de 100× ilâ 1.000.000× arasında ya da daha fazladır. Taramalı tünelleme mikroskopları ise, keskin metal ucundan üzerinde çalışılan malzemeye kuantum tünelleme ile elektronlar yollayarak malzeme yüzeyinin atomik çözünürlüklü görüntüsünü üretirler.[176][177][178]
Diğer
[değiştir | kaynağı değiştir]Serbest elektron lazerlerinde göreli bir elektron demeti, alanları değişken yönleri gösteren dipol mıknatısları sırasının meydana getirdiği salındırıcıdan geçer. Elektronlar, rezonans frekansında radyasyon alanını güçlendirmek için aynı elektronlarla uyumlu olarak etkileşime giren sinkrotron radyasyonu yayarlar. Serbest elektron lazerleri, geniş frekanslarla, mikrodalgalardan hafif X ışınlarına uyumlu yüksek radyans derecesine sahip elektromanyetik radyasyon yayımı gerçekleştirebilirler. Bu araçlar; imalat ve iletişimin yanı sıra yumuşak doku cerrahisi gibi çeşitli tıbbi alanlarla kullanılır.[179]
Elektronlar; laboratuvar araçları, bilgisayar ekranları ve televizyon alıcılarında çoğunlukla görüntüleme aracı olarak kullanılan katot ışını tüpleri için önemlidirler.[180] Fotomultiper tüplerde fotokatoda çarpan her foton, saptanabilir bir akım darbesi üreten bir elektron yayılımı başlatır.[181] Vakum tüpleri, elektron akışını, elektrik sinyallerini idare etmek için kullansa da; yerlerini transistör gibi katı hâl aletlerine bırakmışlardır.[182]
Notlar
[değiştir | kaynağı değiştir]- ^ Kesirli sürümün böleni, ondalık değerin tersidir (4,2×10-13 u göreli standart belirsizlik değeri ile birlikte).
- ^ Elektronun yükü, temel yükün negatifidir.
- ^ Bu büyüklük, spin kuantum sayısından şu şekilde elde edilir:
- ^ Bohr magnetonu:
- ^ Klasik elektron yarıçapı değerine şu şekilde ulaşılır: Elektronun yükünün, küresel yapısına eşit olarak dağıldığı varsayılır. Kürenin bir bölümü diğer bölümlerini iteceğinden, kürede bir elektrostatik potansiyel enerji olacaktır. Bu enerjinin, özel görelilik ile tanımlanan (E = mc2) elektronun durgun enerjisine eşit olduğu düşünülür. Elektrostatik teoriden, kürenin potansiyel enerjisi, yarıçapı r ve yükü e olmak üzere şu şekildedir:
- ^ Göreli olmayan elektronlardan yayılan radyasyonlar da bazı kaynaklarda sinkrotron radyasyonu olarak adlandırılır.
- ^ Dalga boyundaki değişim (Δλ), saçılma açısına (θ) bağlıdır ve matematiksel gösterimi şu şekildedir:
Kaynakça
[değiştir | kaynağı değiştir]- Özel
- ^ a b Benjamin, Park (1898). A History of Electricity (İngilizce). New York: Wiley. ss. 315, 484-485. ISBN 978-1313106054.
- ^ a b Cresswell, Julia (2010). Oxford Dictionary of Word Origins (İngilizce). Oxford University Press. s. 147. ISBN 0199547939.
- ^ a b Chen, E. C. M.; Chen, E. S. D. (2004). The Electron Capture Detector and The Study of Reactions With Thermal Electrons (İngilizce). New York: Wiley. s. 4. ISBN 0471659886.
- ^ "Elektrik". Nişanyan Sözlük. 31 Ocak 2022 tarihinde kaynağından arşivlendi.
- ^ Keithley, Joseph F. (1999). The Story of Electrical and Magnetic Measurements (İngilizce). IEEE Press. ss. 15, 20. ISBN 978-0-7803-1193-0.
- ^ Cajori, Florian (1917). A History of Physics in Its Elementary Branches (İngilizce). Macmillan. s. 118.
- ^ McKenzie, A. E. E. (1961). Magnetism and Electricity (İngilizce). Cambridge: Cambridge University Press. s. 25.
- ^ Myers, Rusty L. (2006). The Basics of Physics (İngilizce). Greenwood Publishing Group. s. 242. ISBN 978-0-313-32857-2.
- ^ Farrar, W. V. (1969). "Richard Laming and the coal-gas industry, with his views on the structure of matter". Annals of Science (İngilizce). 25 (3): 243-254. doi:10.1080/00033796900200141.
- ^ Barrow, John D. (1983). "Natural Units Before Planck". Quarterly Journal of the Royal Astronomical Society (İngilizce). 24: 24-26. Bibcode:1983QJRAS..24...24B. ISSN 0035-8738.
- ^ Arabatzis, Theodore (2006). Representing Electrons (İngilizce). University of Chicago Press. ss. 70-74, 96. ISBN 978-0-226-02421-9.
- ^ Okamura, Sōgo (1994). History of Electron Tubes (İngilizce). IOS Press. s. 11. ISBN 978-90-5199-145-1.
- ^ Stoney, G. J. (1894). "Of the "electron," or atom of electricity". Philosophical Magazine (İngilizce). 38 (5): 418-420. doi:10.1080/14786449408620653.
- ^ ""electron, n.2"". Oxford English Dictionary (İngilizce). Oxford University Press. 27 Temmuz 2020 tarihinde kaynağından arşivlendi.
- ^ Soukhanov, A. H., (Ed.) (1986). Word Mysteries & Histories (İngilizce). Houghton Mifflin Company. s. 73. ISBN 978-0-395-40265-8.
- ^ Guralnik, D. B., (Ed.) (1970). Webster's New World Dictionary (İngilizce). Prentice Hall. s. 450.
- ^ a b c Thomson, J. J. (2005). Conduction of Electricity Through Gases (İngilizce). Watchmaker Publishing. s. 621-622. ISBN 1929148496.
- ^ Whittaker, E. T. (1951). A History of the Theories of Aether and Electricity (İngilizce). 1. Londra: Nelson. s. 393.
- ^ a b c Leicester, H. M. (1971). The Historical Background of Chemistry (İngilizce). Courier Dover. ss. 221-222. ISBN 978-0-486-61053-5.
- ^ DeKosky, R. K. (1983). "William Crookes and the quest for absolute vacuum in the 1870s". Annals of Science (İngilizce). 40 (1): 1-18. doi:10.1080/00033798300200101.
- ^ Zeeman, P. (1907). Lockyer, Norman (Ed.). "Sir William Crookes, F.R.S". Nature (İngilizce). 77 (1984): 1-3. Bibcode:1907Natur..77....1C. doi:10.1038/077001a0.
- ^ Wilczek, Frank (1 Haziran 2012). "Happy Birthday, Electron". Scientific American (İngilizce). ISSN 0036-8733. 1 Kasım 2013 tarihinde kaynağından arşivlendi. Erişim tarihi: 8 Ekim 2018.
- ^ Rechenberg, Helmut (2001). The Historical Development of Quantum Theory (İngilizce). Springer. s. 631. ISBN 038795175X.
- ^ Chmielewski, A. G.; Haji-Saeid, M. (Eylül-Ekim 2004). "Radiation technologies: past, present and future". Radiation Physics and Chemistry (İngilizce). 71 (1-2): 17-21. doi:10.1016/j.radphyschem.2004.05.040.
- ^ Trenn, T. J. (1976). "Rutherford on the Alpha-Beta-Gamma Classification of Radioactive Rays". Isis (İngilizce). 67 (1): 61-75. doi:10.1086/351545. JSTOR 231134.
- ^ Becquerel, Henri (1900). "Déviation du Rayonnement du Radium dans un Champ Électrique". Comptes rendus de l'Académie des sciences (Fransızca). 130: 809-815.
- ^ Buchwald, J. Z.; Warwick, A. (2001). Histories of the Electron (İngilizce). MIT Press. ss. 90-91. ISBN 978-0-262-52424-7.
- ^ Myers, W. G. (1976). "Becquerel's Discovery of Radioactivity in 1896". The Journal of Nuclear Medicine (İngilizce). 17 (7): 579-582. PMID 775027.
- ^ a b c d Thomson, J. J. (1897). "Cathode Rays". Philosophical Magazine (İngilizce). 44 (269): 293-316. doi:10.1080/14786449708621070.
- ^ O'Hara, J. G. (Mart 1975). "George Johnstone Stoney, F.R.S., and the concept of the electron". Notes and Records (İngilizce). 29 (2): 265-276. doi:10.1098/rsnr.1975.0018. JSTOR 531468.
- ^ Kikoin, İ. K.; Sominski, İ. S. (1961). "Abram Fedorovich Ioffe (on his eightieth birthday)". Soviet Physics Uspekhi (İngilizce). 3 (5): 798-809. Bibcode:1961SvPhU...3..798K. doi:10.1070/PU1961v003n05ABEH005812.
- ^ Das Gupta, N. N.; Ghosh, S. K. (1999). "A Report on the Wilson Cloud Chamber and Its Applications in Physics". Reviews of Modern Physics (İngilizce). 18 (2): 225-290. Bibcode:1946RvMP...18..225G. doi:10.1103/RevModPhys.18.225.
- ^ a b c Smirnov, B. M. (2003). Physics of Atoms and Ions (İngilizce). Springer. ss. 14-21. ISBN 978-0-387-95550-6.
- ^ Pais, Abraham (1991). Niels Bohr's Times, In Physics, Philosophy and Polity (İngilizce). Oxford: Clarendon Press. ss. 146-149. ISBN 978-0-19-852049-8.
- ^ Lewis, Gilbert (1916). "The Atom and the Molecule". Journal of the American Chemical Society (İngilizce). 38 (4): 762-786. doi:10.1021/ja02261a002.
- ^ Arabatzis, T.; Gavroglu, K. (1997). "The chemists' electron". European Journal of Physics (İngilizce). 18 (3): 150-163. Bibcode:1997EJPh...18..150A. doi:10.1088/0143-0807/18/3/005.
- ^ Langmuir, Irving (1919). "The arrangement of electrons in atoms and molecules". Journal of the American Chemical Society (İngilizce). 41 (6): 868-934. doi:10.1021/ja02227a002.
- ^ Scerri, E. R. (2007). The Periodic Table (İngilizce). Oxford University Press. ss. 205-226. ISBN 978-0-19-530573-9.
- ^ Massimi, Michela (2005). Pauli's Exclusion Principle (İngilizce). Cambridge University Press. ss. 7-8. ISBN 978-0-521-83911-2.
- ^ Uhlenbeck, G. E.; Goudsmith, S. (1925). "Ersetzung der Hypothese vom unmechanischen Zwang durch eine Forderung bezüglich des inneren Verhaltens jedes einzelnen Elektrons". Naturwissenschaften (Almanca). 13 (47): 953-954. Bibcode:1925NW.....13..953E. doi:10.1007/BF01558878.
- ^ Pauli, Wolfgang (1923). "Über die Gesetzmäßigkeiten des anomalen Zeemaneffektes". Zeitschrift für Physik (Almanca). 16 (1): 155-164. Bibcode:1923ZPhy...16..155P. doi:10.1007/BF01327386.
- ^ Karplus, Robert (1969). Introductory Physics (İngilizce). W. A. Cummings. s. 217. 21 Ağustos 2021 tarihinde kaynağından arşivlendi. Erişim tarihi: 3 Ekim 2019.
- ^ Falkenburg, Brigette (2007). Particle Metaphysics (İngilizce). Springer. s. 85. ISBN 978-3-540-33731-7.
- ^ Thomson, G. P.; Reid, A. (18 Haziran 1927). "Diffraction of Cathode Rays by a Thin Film". Nature (İngilizce). 119 (3007): 890. doi:10.1038/119890a0.
- ^ "Lester Halbert Germer". Encyclopædia Britannica (İngilizce). 23 Ocak 2019 tarihinde kaynağından arşivlendi. Erişim tarihi: 3 Ekim 2019.
- ^ Schrödinger, Erwin (1926). "Quantisierung als Eigenwertproblem". Annalen der Physik (Almanca). 385 (13): 437-490. Bibcode:1926AnP...385..437S. doi:10.1002/andp.19263851302.
- ^ Rigden, J. S. (2003). Hydrogen (İngilizce). Harvard University Press. ss. 59-86. ISBN 978-0-674-01252-3.
- ^ Reed, B. C. (2007). Quantum Mechanics (İngilizce). Jones & Bartlett Publishers. ss. 275-350. ISBN 978-0-7637-4451-9.
- ^ Dirac, P. A. M. (1928). "The quantum theory of the electron". Proceedings of the Royal Society A (İngilizce). 117 (778): 610-624. Bibcode:1928RSPSA.117..610D. doi:10.1098/rspa.1928.0023.
- ^ Dirac, Paul (1930). "A theory of electrons and protons". Proceedings of the Royal Society A (İngilizce). Royal Society Publishing. 126 (801): 360-365. Bibcode:1930RSPSA.126..360D. doi:10.1098/rspa.1930.0013. JSTOR 95359.
- ^ Greiner, Walter (2000). Relativistic Quantum Mechanics. Wave Equations (İngilizce) (3. bas.). Springer. ISBN 3-5406-74578. 22 Nisan 2019 tarihinde kaynağından arşivlendi. Erişim tarihi: 3 Ekim 2019.
- ^ Anderson, C. D. (1933). "The Positive Electron". Physical Review (İngilizce). 43 (6): 491-494. Bibcode:1933PhRv...43..491A. doi:10.1103/PhysRev.43.491.
- ^ Lamb, Willis E.; Retherford, Robert C. (1947). "Fine Structure of the Hydrogen Atom by a Microwave Method". Physical Review (İngilizce). 72 (3): 241-243. Bibcode:1947PhRv...72..241L. doi:10.1103/PhysRev.72.241.
- ^ Kusch, P.; Foley, H. M. (1948). "The Magnetic Moment of the Electron". Physical Review (İngilizce). 74: 250. Bibcode:1948PhRv...74..250R. doi:10.1103/PhysRev.74.250.
- ^ Schwinger, Julian (1948). "On Quantum-Electrodynamics and the Magnetic Moment of the Electron". Physical Review (İngilizce). 73 (4): 416. Bibcode:1948PhRv...73..416S. doi:10.1103/PhysRev.73.416.
- ^ Panofsky, Wolfgang K. H. (1997). "The Evolution of Particle Accelerators & Colliders" (PDF) (İngilizce). Stanford Üniversitesi. 3 Haziran 2016 tarihinde kaynağından arşivlendi (PDF). Erişim tarihi: 14 Ekim 2018.
- ^ Kerst, D. W. (1940). "Acceleration of Electrons by Magnetic Induction". Physical Review (İngilizce). 58 (9): 841. Bibcode:1940PhRv...58..841K. doi:10.1103/PhysRev.58.841.
- ^ Elder, F. R.; Gurewitsch, A. M.; Langmuir, R. V.; Pollock, H. C. (1947). "Radiation from Electrons in a Synchrotron". Physical Review (İngilizce). 71 (11): 829-830. Bibcode:1947PhRv...71..829E. doi:10.1103/PhysRev.71.829.5.
- ^ Hoddeson, Lillian; Brown, Laurie; Riordan, Michael; Dresden, Max, (Ed.) (1997). The Rise of the Standard Model (İngilizce). Cambridge University Press. ss. 25-26. ISBN 978-0-521-57816-5.
- ^ Bernardini, Carlo (2004). "AdA: The First Electron-Positron Collider". Physics in Perspective (İngilizce). 6 (2): 156-183. Bibcode:2004PhP.....6..156B. doi:10.1007/s00016-003-0202-y.
- ^ "Testing the Standard Model: The LEP experiments" (İngilizce). Avrupa Nükleer Araştırma Merkezi. 2008. 13 Şubat 2013 tarihinde kaynağından arşivlendi. Erişim tarihi: 14 Ekim 2018.
- ^ "LEP reaps a final harvest". CERN Courier (İngilizce). 40 (10). 2000. 21 Kasım 2010 tarihinde kaynağından arşivlendi. Erişim tarihi: 14 Ekim 2018.
- ^ Frampton; Hung, P. Q.; Sher, Marc (2000). "Quarks and leptons beyond the third generation". Physics Reports (İngilizce). 330 (5-6): 263-348. arXiv:hep-ph/9903387 $2. Bibcode:2000PhR...330..263F. doi:10.1016/S0370-1573(99)00095-2.
- ^ a b Raith, W.; Mulvey, T. (2001). Constituents of Matter (İngilizce). CRC Press. ss. 777-781. ISBN 978-0-8493-1202-1.
- ^ a b c d e f g h Tiesinga, Eite; Mohr, Peter J.; Newell, David B.; Taylor, Barry N. (2021). "CODATA Recommended Values of the Fundamental Physical Constants: 2018". Journal of Physical and Chemical Reference Data (İngilizce). 50: 033105. doi:10.1103/RevModPhys.93.025010.
- ^ Murphy, M. T. (2008). "Strong limit on a variable proton-to-electron mass ratio from molecules in the distant universe". Science (İngilizce). 320 (5883): 1611-1613. arXiv:0806.3081 $2. Bibcode:2008Sci...320.1611M. doi:10.1126/science.1156352. PMID 18566280.
- ^ Zorn, J. C.; Chamberlain, G. E.; Hughes, V. W. (1963). "Experimental limits for the electron-proton charge difference and for the charge of the neutron". Physical Review (İngilizce). 129 (6): 2566-2576. Bibcode:1963PhRv..129.2566Z. doi:10.1103/PhysRev.129.2566.
- ^ Gupta, M. C. (2001). Atomic and Molecular Spectroscopy (İngilizce). New Age Publishers. s. 81. ISBN 978-81-224-1300-7.
- ^ a b Odom, B. (2006). "New Measurement of the Electron Magnetic Moment Using a One-Electron Quantum Cyclotron". Physical Review Letters (İngilizce). 97 (3): 030801. Bibcode:2006PhRvL..97c0801O. doi:10.1103/PhysRevLett.97.030801. PMID 16907490.
- ^ Anastopoulos, C. (200). Particle or Wave (İngilizce). Princeton University Press. ss. 261-262. ISBN 978-0-691-13512-0.
- ^ Eichten, E. J.; Peskin, M. E.; Peskin, M. (1983). "New tests for quark and lepton substructure". Physical Review Letters (İngilizce). 50 (11): 811-814. Bibcode:1983PhRvL..50..811E. doi:10.1103/PhysRevLett.50.811.
- ^ Gabrielse, G. (2006). "New Determination of the Fine Structure Constant from the Electron g Value and QED". Physical Review Letters (İngilizce). 97 (3): 030802(1-4). Bibcode:2006PhRvL..97c0802G. doi:10.1103/PhysRevLett.97.030802. PMID 16907491.
- ^ a b Curtis, L. J. (2003). Atomic Structure and Lifetimes (İngilizce). Cambridge University Press. s. 74. ISBN 978-0-521-53635-6.
- ^ Dehmelt, H. (1988). "A Single Atomic Particle Forever Floating at Rest in Free Space: New Value for Electron Radius". Physica Scripta (İngilizce). T22: 102-110. Bibcode:1988PhST...22..102D. doi:10.1088/0031-8949/1988/T22/016.
- ^ Gabrielse, Gerald. "Limit on Electron Substructure" (İngilizce). Harvard Üniversitesi. 10 Nisan 2019 tarihinde kaynağından arşivlendi. Erişim tarihi: 7 Ekim 2019.
- ^ Meschede, D. (2004). Optics, Light and Lasers (İngilizce). Wiley-VCH. s. 168. ISBN 978-3-527-40364-6.
- ^ Haken, H.; Wolf, H. C.; Brewer, W. D. (2005). The Physics of Atoms and Quanta (İngilizce). Springer. s. 70. ISBN 978-3-540-67274-6.
- ^ Steinberg, R. I. (1999). "Experimental test of charge conservation and the stability of the electron". Physical Review D (İngilizce). 61 (2): 2582-2586. Bibcode:1975PhRvD..12.2582S. doi:10.1103/PhysRevD.12.2582.
- ^ Agostini, M.; ve diğerleri. (Borexino işbirliği) (2015). "Test of Electric Charge Conservation with Borexino". Physical Review Letters (İngilizce). 115 (23): 231802. arXiv:1509.01223 $2. Bibcode:2015PhRvL.115w1802A. doi:10.1103/PhysRevLett.115.231802. PMID 26684111.
- ^ Beringer, J. (Particle Data Group) (2012). "Review of Particle Physics: [electron properties]" (PDF). Physical Review D (İngilizce). 86 (1): 010001. Bibcode:2012PhRvD..86a0001B. doi:10.1103/PhysRevD.86.010001. 3 Mart 2016 tarihinde kaynağından arşivlendi (PDF). Erişim tarihi: 9 Kasım 2018.
- ^ Back, H. O. (2002). "Search for electron decay mode e → γ + ν with prototype of Borexino detector". Physics Letters B (İngilizce). 525 (1-2): 29-40. Bibcode:2002PhLB..525...29B. doi:10.1016/S0370-2693(01)01440-X.
- ^ Feynman, Richard P.; Leighton, Robert B.; Sands, Matthew (1965). The Feynman Lectures on Physics (İngilizce). 3. Addison-Wesley. s. 15. ISBN 978-0201021189.
- ^ a b c d Munowitz, M. (2005). Knowing, The Nature of Physical Law (İngilizce). Oxford University Press. ss. 162-218. ISBN 978-0-19-516737-5.
- ^ Kane, Gordon (9 Ekim 2006). "Are virtual particles really constantly popping in and out of existence? Or are they merely a mathematical bookkeeping device for quantum mechanics?". Scientific American (İngilizce). 19 Eylül 2019 tarihinde kaynağından arşivlendi. Erişim tarihi: 15 Ekim 2019.
- ^ Taylor, J. (1989). "Gauge Theories in Particle Physics". Davies, Paul (Ed.). The New Physics (İngilizce). Cambridge University Press. s. 464. ISBN 978-0-521-43831-5.
- ^ a b Genz, H. (2001). Nothingness (İngilizce). Da Capo Press. ss. 241-243, 245-247. ISBN 978-0-7382-0610-3.
- ^ Gribbin, J. (25 Ocak 1997). "More to electrons than meets the eye". New Scientist (İngilizce). 11 Şubat 2015 tarihinde kaynağından arşivlendi. Erişim tarihi: 21 Kasım 2018.
- ^ Levine, I. (1997). "Measurement of the Electromagnetic Coupling at Large Momentum Transfer". Physical Review Letters (İngilizce). 78 (3): 424-427. Bibcode:1997PhRvL..78..424L. doi:10.1103/PhysRevLett.78.424.
- ^ Murayama, H. (10-17 Mart 2006). Supersymmetry Breaking Made Easy, Viable and Generic. Proceedings of the XLIInd Rencontres de Moriond on Electroweak Interactions and Unified Theories (İngilizce). La Thuile. arXiv:0709.3041 $2. Bibcode:2007arXiv0709.3041M.
- ^ Schwinger, J. (1948). "On Quantum-Electrodynamics and the Magnetic Moment of the Electron". Physical Review (İngilizce). 73 (4): 416-417. Bibcode:1948PhRv...73..416S. doi:10.1103/PhysRev.73.416.
- ^ Foldy, L. L.; Wouthuysen, S. (1950). "On the Dirac Theory of Spin 1/2 Particles and Its Non-Relativistic Limit". Physical Review (İngilizce). 78 (1): 29-36. Bibcode:1950PhRv...78...29F. doi:10.1103/PhysRev.78.29.
- ^ Sidharth, B. G. (2009). "Revisiting Zitterbewegung". International Journal of Theoretical Physics (İngilizce). 48 (2): 497-506. arXiv:0806.0985 $2. Bibcode:2009IJTP...48..497S. doi:10.1007/s10773-008-9825-8.
- ^ Griffiths 1998, ss. 58-61.
- ^ Crowell, Benjamin (2000). Electricity and Magnetism (Light And Matter, Book 4) (İngilizce). Light and Matter. ss. 129-152. ISBN 978-0-9704670-4-1.
- ^ Griffiths 1998, s. 429-434.
- ^ Munowitz 2005, s. 160.
- ^ Mahadevan, R.; Narayan, R.; Yi, I. (1996). "Harmony in Electrons: Cyclotron and Synchrotron Emission by Thermal Electrons in a Magnetic Field". The Astrophysical Journal (İngilizce). 465: 327-337. arXiv:astro-ph/9601073 $2. Bibcode:1996ApJ...465..327M. doi:10.1086/177422.
- ^ Rohrlich, F. (1999). "The Self-Force and Radiation Reaction". American Journal of Physics (İngilizce). 68 (12): 1109-1112. Bibcode:2000AmJPh..68.1109R. doi:10.1119/1.1286430.
- ^ Georgi, H. (1989). "Grand Unified Theories". Davies, Paul (Ed.). The New Physics (İngilizce). Cambridge University Press. s. 427. ISBN 978-0-521-43831-5.
- ^ Blumenthal, G. J.; Gould, R. (1970). "Bremsstrahlung, Synchrotron Radiation, and Compton Scattering of High-Energy Electrons Traversing Dilute Gases". Reviews of Modern Physics (İngilizce). 42 (2): 237-270. Bibcode:1970RvMP...42..237B. doi:10.1103/RevModPhys.42.237.
- ^ Zombeck 2007, ss. 393, 396.
- ^ Chen, S. -Y.; Maksimchuk, A.; Umstadter, D. (1998). "Experimental observation of relativistic nonlinear Thomson scattering". Nature (İngilizce). 396 (6712): 653-655. arXiv:physics/9810036 $2. Bibcode:1998Natur.396..653C. doi:10.1038/25303.
- ^ Beringer, R.; Montgomery, C. G. (1942). "The Angular Distribution of Positron Annihilation Radiation". Physical Review (İngilizce). 61 (5-6): 222-224. Bibcode:1942PhRv...61..222B. doi:10.1103/PhysRev.61.222.
- ^ Buffa, A. (2000). College Physics (İngilizce) (4. bas.). Prentice Hall. s. 888. ISBN 978-0-13-082444-8.
- ^ Eichler, J. (2005). "Electron–positron pair production in relativistic ion–atom collisions". Physics Letters A (İngilizce). 347 (1-3): 67-72. Bibcode:2005PhLA..347...67E. doi:10.1016/j.physleta.2005.06.105.
- ^ Hubbell, J. H. (2006). "Electron positron pair production by photons: A historical overview". Radiation Physics and Chemistry (İngilizce). 75 (6): 614-623. Bibcode:2006RaPC...75..614H. doi:10.1016/j.radphyschem.2005.10.008.
- ^ Quigg, C. (4-30 Haziran 2000). The Electroweak Theory. TASI 2000: Flavor Physics for the Millennium (İngilizce). Boulder, Colorado. s. 80. arXiv:hep-ph/0204104 $2. Bibcode:2002hep.ph....4104Q.
- ^ Hall, Peter Joseph (1986). "The Pauli exclusion principle and the foundations of chemistry". Synthese (İngilizce). 69 (3): 267-272. doi:10.1007/BF00413974.
- ^ Mulliken, R. S. (1967). "Spectroscopy, Molecular Orbitals, and Chemical Bonding". Science (İngilizce). 157 (3784): 13-24. Bibcode:1967Sci...157...13M. doi:10.1126/science.157.3784.13. PMID 5338306.
- ^ Burhop, Eric (1952). The Auger Effect and Other Radiationless Transitions (İngilizce). Cambridge University Press. ss. 2-3. ISBN 978-0-88275-966-1.
- ^ a b Grupen, C. (2000). "Physics of Particle Detection". AIP Conference Proceedings (İngilizce). 536: 3-34. arXiv:physics/9906063 $2. doi:10.1063/1.1361756.
- ^ Jiles, D. (1998). Introduction to Magnetism and Magnetic Materials (İngilizce). CRC Press. ss. 280-287. ISBN 978-0-412-79860-3.
- ^ Löwdin, P. O.; Erkki Brändas, E.; Kryachko, E. S. (2003). Fundamental World of Quantum Chemistry (İngilizce). Springer. ss. 393-394. ISBN 978-1-4020-1290-7.
- ^ Pauling, L. C. (1960). The Nature of the Chemical Bond and the Structure of Molecules and Crystals (İngilizce) (3. bas.). Cornell University Press. ss. 4-10. ISBN 978-0-8014-0333-0.
- ^ McQuarrie, D. A.; Simon, J. D. (1997). Physical Chemistry (İngilizce). University Science Books. ss. 325-361. ISBN 978-0-935702-99-6.
- ^ Daudel, R. (1974). "The Electron Pair in Chemistry". Canadian Journal of Chemistry (İngilizce). 52 (8): 1310-1320. doi:10.1139/v74-201.
- ^ Rakov, V. A.; Uman, M. A. (2007). Lightning (İngilizce). Cambridge University Press. s. 4. ISBN 978-0-521-03541-5.
- ^ Freeman, G. R.; March, N. H. (1999). "Triboelectricity and some associated phenomena". Materials Science and Technology (İngilizce). 15 (12): 1454-1458. doi:10.1179/026708399101505464.
- ^ Forward, K. M.; Lacks, D. J.; Sankaran, R. M. (2009). "Methodology for studying particle–particle triboelectrification in granular materials". Journal of Electrostatics (İngilizce). 67 (2-3): 178-183. doi:10.1016/j.elstat.2008.12.002.
- ^ Weinberg, S. (2003). The Discovery of Subatomic Particles (İngilizce). Cambridge University Press. ss. 15-16. ISBN 978-0-521-82351-7.
- ^ Lou, L. -F. (2003). Introduction to Phonons and Electrons (İngilizce). World Scientific. ss. 162, 164. ISBN 978-981-238-461-4.
- ^ Guru, B. S.; Hızıroğlu, H. R. (2004). Electromagnetic Field Theory (İngilizce). Cambridge University Press. ss. 138, 276. ISBN 978-0-521-83016-4.
- ^ Achuthan, M. K.; Bhat, K. N. (2007). Fundamentals of Semiconductor Devices (İngilizce). Tata McGraw-Hill Education. ss. 49-67. ISBN 978-0-07-061220-4.
- ^ a b Ziman, J. M. (2001). Electrons and Phonons (İngilizce). Oxford University Press. s. 260. ISBN 978-0-19-850779-6.
- ^ Main, P. (12 Haziran 1993). "When electrons go with the flow: Remove the obstacles that create electrical resistance, and you get ballistic electrons and a quantum surprise". New Scientist (İngilizce). 1887: 30. 11 Şubat 2015 tarihinde kaynağından arşivlendi. Erişim tarihi: 8 Ocak 2019.
- ^ Blackwell, G. R. (2000). The Electronic Packaging Handbook (İngilizce). CRC Press. ss. 6.39-6.40. ISBN 978-0-8493-8591-9.
- ^ Durrant, A. (2000). Quantum Physics of Matter (İngilizce). CRC Press. ss. 43, 71-78. ISBN 978-0-7503-0721-5. 27 Mayıs 2016 tarihinde kaynağından arşivlendi. Erişim tarihi: 8 Ocak 2019.
- ^ Kadin, A. M. (2007). "Spatial Structure of the Cooper Pair". Journal of Superconductivity and Novel Magnetism (İngilizce). 20 (4): 285-292. arXiv:cond-mat/0510279 $2. doi:10.1007/s10948-006-0198-z.
- ^ "Discovery About Behavior Of Building Block Of Nature Could Lead To Computer Revolution". Science Daily (İngilizce). 31 Temmuz 2009. 3 Haziran 2019 tarihinde kaynağından arşivlendi. Erişim tarihi: 28 Ekim 2019.
- ^ Jompol, Y. (2009). "Probing Spin-Charge Separation in a Tomonaga-Luttinger Liquid". Science (İngilizce). 325 (5940): 597-601. arXiv:1002.2782 $2. Bibcode:2009Sci...325..597J. doi:10.1126/science.1171769. PMID 19644117.
- ^ Çerenkov, Pavel (1934). "Visible emission of clean liquids by action of γ radiation". Dokladı Akademii Nauk SSSR. 2: 451.
- ^ Tamm, I. E.; Frank, I. M. (1937). "Coherent radiation of fast electrons". Proceedings of the USSR Academy of Sciences (İngilizce). 14 (3): 107-112.
- ^ "Special Relativity" (İngilizce). SLAC Ulusal Hızlandırıcı Laboratuvarı. 26 Ağustos 2008. 12 Aralık 2011 tarihinde kaynağından arşivlendi. Erişim tarihi: 24 Ekim 2018.
- ^ Resnick, R.; Eisberg, R. (1985). Quantum Physics of Atoms, Molecules, Solids, Nuclei and Particles (İngilizce) (2. bas.). New York: John Wiley & Sons. ISBN 978-0-471-87373-0.
- ^ Adams, S. (2000). Frontiers (İngilizce). CRC Press. s. 215. ISBN 978-0-7484-0840-5.
- ^ Silk, J. (2000). The Big Bang (İngilizce) (3. bas.). Macmillan. ss. 110-112, 134-137. ISBN 978-0-8050-7256-3.
- ^ Kolb, E. W.; Wolfram, Stephen (1980). "The Development of Baryon Asymmetry in the Early Universe". Physics Letters B (İngilizce). 91 (2): 217-221. Bibcode:1980PhLB...91..217K. doi:10.1016/0370-2693(80)90435-9.
- ^ Sather, E. (1996) [İlkbahar-Yaz]. "The Mystery of Matter Asymmetry" (PDF). Beam Line (İngilizce). Stanford Üniversitesi. 20 Temmuz 2018 tarihinde kaynağından arşivlendi (PDF). Erişim tarihi: 30 Ekim 2019.
- ^ Burles, S.; Nollett, K. M.; Turner, M. S. (1999), Big-Bang Nucleosynthesis (İngilizce), arXiv:astro-ph/9903300 $2
- ^ Boesgaard, A. M.; Steigman, G. (1985). "Big bang nucleosynthesis – Theories and observations". Annual Review of Astronomy and Astrophysics (İngilizce). 23 (2): 319-378. Bibcode:1985ARA&A..23..319B. doi:10.1146/annurev.aa.23.090185.001535.
- ^ a b Barkana, R. (2006). "The First Stars in the Universe and Cosmic Reionization". Science (İngilizce). 313 (5789): 931-934. arXiv:astro-ph/0608450 $2. Bibcode:2006Sci...313..931B. CiteSeerX 10.1.1.256.7276 $2. doi:10.1126/science.1125644. PMID 16917052.
- ^ Burbidge, E. M. (1957). "Synthesis of Elements in Stars" (PDF). Reviews of Modern Physics (İngilizce). 29 (4): 548-647. Bibcode:1957RvMP...29..547B. doi:10.1103/RevModPhys.29.547. 23 Temmuz 2018 tarihinde kaynağından arşivlendi (PDF). Erişim tarihi: 31 Ekim 2019.
- ^ Rodberg, L. S.; Weisskopf, V. (1957). "Fall of Parity: Recent Discoveries Related to Symmetry of Laws of Nature". Science (İngilizce). 125 (3249): 627-633. Bibcode:1957Sci...125..627R. doi:10.1126/science.125.3249.627. PMID 17810563.
- ^ Fryer, C. L. (1999). "Mass Limits For Black Hole Formation". The Astrophysical Journal (İngilizce). 522 (1): 413-418. arXiv:astro-ph/9902315 $2. Bibcode:1999ApJ...522..413F. doi:10.1086/307647.
- ^ Hutchinson, John; Stojkovic, Dejan (2016). "Icezones instead of firewalls: extended entanglement beyond the event horizon and unitary evaporation of a black hole". Classical and Quantum Gravity (İngilizce). 33 (13): 135006. doi:10.1088/0264-9381/33/13/135006.
- ^ Parikh, M. K.; Wilczek, F. (2000). "Hawking Radiation As Tunneling". Physical Review Letters (İngilizce). 85 (24): 5042-5045. arXiv:hep-th/9907001 $2. Bibcode:2000PhRvL..85.5042P. doi:10.1103/PhysRevLett.85.5042. hdl:1874/17028. PMID 11102182.
- ^ Hawking, Stephen W. (1974). "Black hole explosions?". Nature (İngilizce). 248 (5443): 30-31. Bibcode:1974Natur.248...30H. doi:10.1038/248030a0.
- ^ Halzen, F.; Hooper, D. (2002). "High-energy neutrino astronomy: the cosmic ray connection". Reports on Progress in Physics (İngilizce). 66 (7): 1025-1078. arXiv:astro-ph/0204527 $2. Bibcode:2002RPPh...65.1025H. doi:10.1088/0034-4885/65/7/201.
- ^ Ziegler, J. F. (1998). "Terrestrial cosmic ray intensities". IBM Journal of Research and Development (İngilizce). 42 (1): 117-139. Bibcode:1998IBMJ...42..117Z. doi:10.1147/rd.421.0117.
- ^ Sutton, C. (4 Ağustos 1990). "Muons, pions and other strange particles". New Scientist (İngilizce). 11 Şubat 2015 tarihinde kaynağından arşivlendi. Erişim tarihi: 31 Ekim 2019.
- ^ Wolpert, Stuart (24 Temmuz 2008). "Scientists solve 30-year-old aurora borealis mystery" (İngilizce). Kaliforniya Üniversitesi. 17 Ağustos 2008 tarihinde kaynağından arşivlendi. Erişim tarihi: 31 Ekim 2019.
- ^ Gurnett, Donald A.; Anderson, Roger R. (1976). "Electron Plasma Oscillations Associated with Type III Radio Bursts". Science (İngilizce). 194 (4270): 1159-1162. Bibcode:1976Sci...194.1159G. doi:10.1126/science.194.4270.1159. PMID 17790910.
- ^ Martin, W. C.; Wiese, W. L. (2007). "Atomic Spectroscopy: A Compendium of Basic Ideas, Notation, Data, and Formulas" (İngilizce). Ulusal Standartlar ve Teknoloji Enstitüsü. 23 Şubat 2010 tarihinde kaynağından arşivlendi. Erişim tarihi: 1 Kasım 2019.
- ^ Fowles, Grant R. (1989). Introduction to Modern Optics (İngilizce). Courier Dover. ss. 227-233. ISBN 978-0-486-65957-2.
- ^ Wineland, David; Ekstrom, Philip (1980). "The isolated Electron". Scientific American (İngilizce). 243 (2): 91-101. Bibcode:1980SciAm.243b.104E. doi:10.1038/scientificamerican0880-104.
- ^ Mauritsson, J. (2008). "Coherent Electron Scattering Captured by an Attosecond Quantum Stroboscope". Physical Review Letters (İngilizce). 100 (7): 073003. arXiv:0708.1060 $2. Bibcode:2008PhRvL.100g3003M. doi:10.1103/PhysRevLett.100.073003. PMID 18352546.
- ^ Damascelli, Andrea (2004). "Probing the Electronic Structure of Complex Systems by ARPES". Physica Scripta (İngilizce). T109: 61-74. arXiv:cond-mat/0307085 $2. Bibcode:2004PhST..109...61D. doi:10.1238/Physica.Topical.109a00061.
- ^ "Image # L-1975-02972" (İngilizce). Langley Araştırma Merkezi, NASA. 4 Nisan 1975. 7 Aralık 2008 tarihinde kaynağından arşivlendi. Erişim tarihi: 5 Kasım 2019.
- ^ Elmer, J. (3 Mart 2008). "Standardizing the Art of Electron-Beam Welding" (İngilizce). Lawrence Livermore Ulusal Laboratuvarı. 29 Ağustos 2013 tarihinde kaynağından arşivlendi. Erişim tarihi: 5 Kasım 2019.
- ^ Schultz, H. (1993). Electron Beam Welding (İngilizce). Woodhead Publishing. ss. 2-3. ISBN 978-1-85573-050-2.
- ^ Benedict, G. F. (1987). Nontraditional Manufacturing Processes. Manufacturing engineering and materials processing (İngilizce). 19. CRC Press. s. 273. ISBN 978-0-8247-7352-6.
- ^ Özdemir, F. S. (25-27 Haziran 1979). Electron beam lithography. Proceedings of the 16th Conference on Design automation (İngilizce). San Diego, Kaliforniya: IEEE Press. ss. 383-391.
- ^ Madou, M. J. (2002). Fundamentals of Microfabrication (İngilizce) (2. bas.). CRC Press. ss. 53-54. ISBN 978-0-8493-0826-0.
- ^ Jongen, Y.; Herer, A. (2-5 Mayıs 1996). Electron Beam Scanning in Industrial Applications. APS/AAPT Joint Meeting (İngilizce). Amerikan Fizik Topluluğu. Bibcode:1996APS..MAY.H9902J.
- ^ Mobus, G. (2010). "Nano-scale quasi-melting of alkali-borosilicate glasses under electron irradiation". Journal of Nuclear Materials (İngilizce). 396 (2-3): 264-271. Bibcode:2010JNuM..396..264M. doi:10.1016/j.jnucmat.2009.11.020.
- ^ Beddar, A. S.; Domanovic, Mary Ann; Kubu, Mary Lou; Ellis, Rod J.; Sibata, Claudio H.; Kinsella, Timothy J. (2001). "Mobile linear accelerators for intraoperative radiation therapy". AORN Journal (İngilizce). 74 (5): 700-705. doi:10.1016/S0001-2092(06)61769-9.
- ^ Gazda, M. J.; Coia, L. R. (1 Haziran 2007). "Principles of Radiation Therapy" (PDF) (İngilizce). 5 Ekim 2018 tarihinde kaynağından (PDF) arşivlendi. Erişim tarihi: 6 Kasım 2019.
- ^ Chao, A. W.; Tigner, M. (1999). Handbook of Accelerator Physics and Engineering (İngilizce). World Scientific. ss. 155, 188. ISBN 978-981-02-3500-0.
- ^ Oura, K. (2003). Surface Science (İngilizce). Springer. ss. 1-45. ISBN 978-3-540-00545-2.
- ^ Ichimiya, A.; Cohen, P. I. (2004). Reflection High-energy Electron Diffraction (İngilizce). Cambridge University Press. s. 1. ISBN 978-0-521-45373-8.
- ^ Heppell, T. A. (1967). "A combined low energy and reflection high energy electron diffraction apparatus". Journal of Scientific Instruments (İngilizce). 44 (9): 686-688. Bibcode:1967JScI...44..686H. doi:10.1088/0950-7671/44/9/311.
- ^ McMullan, D. (1993). "Scanning Electron Microscopy" (İngilizce). Cambridge Üniversitesi. 14 Mayıs 2019 tarihinde kaynağından arşivlendi. Erişim tarihi: 8 Kasım 2019.
- ^ Slayter, H. S. (1992). Light and Electron Microscopy (İngilizce). Cambridge University Press. s. 1. ISBN 978-0-521-33948-3.
- ^ Cember, H. (1996). Introduction to Health Physics (İngilizce). McGraw-Hill Professional. ss. 42-43. ISBN 978-0-07-105461-4.
- ^ Erni, R. (2009). "Atomic-Resolution Imaging with a Sub-50-pm Electron Probe". Physical Review Letters (İngilizce). 102 (9): 096101. Bibcode:2009PhRvL.102i6101E. doi:10.1103/PhysRevLett.102.096101. PMID 19392535.
- ^ Bozzola, J. J.; Russell, L. D. (1999). Electron Microscopy (İngilizce). Jones & Bartlett Publishers. ss. 12, 197-199. ISBN 978-0-7637-0192-5.
- ^ Flegler, S. L.; Heckman Jr., J. W.; Klomparens, K. L. (1995). Scanning and Transmission Electron Microscopy (İngilizce) (yeniden bas.). Oxford University Press. ss. 43-45. ISBN 978-0-19-510751-7.
- ^ Bozzola, J. J.; Russell, L. D. (1999). Electron Microscopy (İngilizce) (2. bas.). Jones & Bartlett Publishers. s. 9. ISBN 978-0-7637-0192-5.
- ^ Freund, H. P.; Antonsen, T. (1996). Principles of Free-Electron Lasers (İngilizce). Springer. ss. 1-30. ISBN 978-0-412-72540-1.
- ^ Kitzmiller, J. W. (1995). Television Picture Tubes and Other Cathode-Ray Tubes (İngilizce). Diane Publishing. ss. 3-5. ISBN 978-0-7881-2100-5.
- ^ Sclater, N. (1999). Electronic Technology Handbook (İngilizce). McGraw-Hill Professional. ss. 227-228. ISBN 978-0-07-058048-0.
- ^ Navarro Sosa, Estanislao. "Electron tube". Encyclopædia Britannica (İngilizce). 14 Nisan 2020 tarihinde kaynağından arşivlendi. Erişim tarihi: 20 Kasım 2019.
- Genel
- Griffiths, David J. (1998). Introduction to Electrodynamics (İngilizce) (3. bas.). Prentice Hall. ISBN 978-0-13-805326-0.
- Zombeck, M. V. (2007). Handbook of Space Astronomy and Astrophysics (İngilizce) (3. bas.). Cambridge University Press. ISBN 978-0-521-78242-5.