Paritet av noll

Pariteten av noll är jämn. Det betyder att i valet mellan jämn och udda, är noll ett jämnt tal.
Det enklaste sättet att bevisa detta är att undersöka hur talet 0 stämmer in på definitionen för jämna tal: Det är en heltalsmultipel av 2, nämligen 0 × 2.[1] Som följd av detta har noll alla de egenskaper som kännetecknar jämna tal: Det är delbart med 2,[2] det är granne på båda sidor med udda nummer (-1 och 1), 0 är summan av ett heltal taget två gånger (0+0=0) och 0 kan delas i två lika stora delar, se bilden till höger.[3]
Varför noll är jämnt
[redigera | redigera wikitext]Standarddefinitionen av jämna tal kan direkt användas för att bevisa att talet noll är jämnt. Ett tal är jämnt om det är en heltalsmultipel av 2. Exempelvis är talet 10 jämnt eftersom det är lika med 5 · 2. På samma sätt är noll jämnt eftersom det är lika med 0 · 2.[4] Ekvivalent med den definitionen är att ett tal är jämnt om man kan dela det i två grupper med lika många i varje. Talet noll är då jämnt eftersom man kan dela det i två grupper med noll i varje.[5]
Man kan också förklara varför noll är jämnt utan att hänvisa till den formella definitionen.[6] Följande förklaringar hänvisar till fundamentala egenskaper hos tal för att beskriva jämna tal och hur de kan appliceras på noll.
Grundläggande förklaringar
[redigera | redigera wikitext]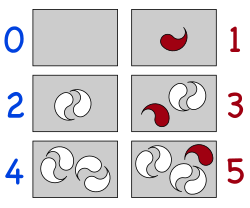
Om man har ett antal objekt kan man använda tal för att beskriva hur många objekten är. Talet noll beskriver då att man inte har några objekt alls. Mer formellt beskriver det den tomma mängden. Om man då kan dela upp objekten i två grupper är talet jämnt när det inte blir något objekt över. Blir det ett objekt över är talet istället udda. Om man har noll objekt kan de delas i två grupper där båda grupperna innehåller noll objekt och det inte heller blir något objekt över, alltså är noll ett jämnt tal.[8] Detta kan illustreras genom att rita objekten i par. Det kan vara svårt att illustrera noll grupper av par eller att det inte då blir något objekt över. Därför kan man rita flera olika antal och jämföra dem med noll. Till exempel för talet fem blir det två par och en som blir över. Alltså är fem udda. För fyra blir det också två par men inget objekt över och fyra är ett jämnt tal. För talet ett blir det inga par men ett objekt över så ett är udda. För noll blir det inget objekt över så noll är jämnt.[9]
Tal kan också visas på en tallinje. Om då udda och jämna tal särskiljs syns tydligt ett mönster, särskilt om också de negativa talen tas med:

Eftersom jämna och udda tal alternerar kan man om man börjar med ett jämnt tal räkna upp eller ner med två i taget alltid nå andra jämna tal och då också noll. Samma sak gäller för udda tal, men då kan noll inte nås.[10]
Livliga diskussioner om det jämna talet noll
[redigera | redigera wikitext]Det har tidvis rått livliga diskussioner på internet och i media om nollan som jämnt tal. Emellanåt blir resultaten av diskussionerna rätt godtyckliga.[11][12][13]
Den amerikanske lingvisten Joseph Grimes menar att frågan "Är noll ett jämnt eller udda tal?" är en bra fråga att ställa till gifta par, om man vill få dem att gräla.[14]
Personer som menar att noll varken är jämnt eller udda använder bevisen för att noll är ett jämnt tal som bevis på att varje regel har sitt undantag.[15][16][17]
Vid millennieskiftet kom ett par ovanliga milstolpar i medialt fokus. Det gällde "1999-11-19" som var det sista datum som inom överskådlig tid bestod av enbart udda siffror. Det gällde vidare "2000-02-02" som var det första datum med enbart jämna siffror som skulle inträffa, på mer än ett årtusende.[18][19][20]
Eftersom dessa påståenden baserades på att noll är ett jämnt tal, opponerade sig många läsare, till exempel:[21]
| ” | … enligt matematiker är noll tillsammans med negativa tal varken udda eller jämnt. | „ |
| ” | Jag håller med om att noll är ett jämnt tal, men räcker det verkligen att säga att beviset är att 0=2x0? Enligt den logiken från en filosofie doktor i matematik, så är noll också udda, eftersom 0=0x1! | „ |
I prov- och testsituationer är det klokt att komma ihåg att noll är ett jämnt tal.[22]

I länder där ransonering enligt udda–jämnt-metoden förekommer, blir frågan om nollan som jämnt tal viktig. Metoden för ransonering används för att halvera förbrukningen, till exempel av drivmedel till bilar. I det fallet får registreringsskylten avgöra. För att fördela drivmedel till halva fordonsparken är det givet att låta 0, 2, 4, 6, 8 på jämnt datum följas av 1, 3, 5, 7, 9 på udda, med noll naturligt placerat bland de jämna talen.
Men 1977 ledde systemet vid en ransonering i Paris till att polisen avvisade förare med registreringsskyltar som slutade med siffran 0, eftersom de var osäkra på om noll var ett jämnt tal.[23][24]
För att undvika sådan förvirring lagstiftar länder ibland att nollan är ett jämnt tal. Det har skett i bland annat Maryland i östra USA och i Nya Sydwales i Australien.[21][25]
På amerikanska flottans fartyg är hytterna på babords sida numrerade med jämna nummer. Noll är dock reserverat för hytter efter centrumlinjen.[26]
I roulette räknas nollan varken som jämn eller udda och ger kasinot en liten fördel.[27] På samma sätt kan regeln om nollan ska räknas som jämnt tal eller inte inverka på oddsen i ett antal olika hasardspel.[28][29][30]
Också leken “Udda och jämnt” påverkas: Om båda spelarna visar noll fingrar blir det totala antalet fingrar noll, varför den spelare som valt jämnt vinner.[31]
Referenser
[redigera | redigera wikitext]- Den här artikeln är helt eller delvis baserad på material från engelskspråkiga Wikipedia, Parity of zero, 7 januari 2015.
- ^ Penner, Robert C. (1999) (på engelska). Discrete Mathematics: Proof Techniques and Mathematical Structures. River Edje: World Scientific. sid. 34. ISBN 981-02-4088-0
- ^ Christer O Kiselman (1993). Jämnt tal. Bokförlaget Bra Böcker AB, Höganäs. sid. 275. ISBN 91-7024-619-X. http://www.ne.se/uppslagsverk/encyklopedi/l%C3%A5ng/j%C3%A4mnt-tal. Läst 15 januari 2015
- ^ Ball, Deborah Loewenberg; Lewis, Jennifer; Thames, Mark Hoover (2008). ”Making mathematics work in school” (på engelska). Journal for Research in Mathematics Education M14: sid. 15. http://www-personal.umich.edu/~dball/articles/BallLewisThames08.pdf. Läst 15 januari 2015.
- ^ Penner 1999, s. 34: Lemma B.2.2, The integer 0 is even and is not odd. Penner uses the mathematical symbol ∃, the existential quantifier, to state the proof: "To see that 0 is even, we must prove that ∃k (0 = 2k), and this follows from the equality 0 = 2 ⋅ 0."
- ^ Dickerson & Pitman 2012, sid. 191.
- ^ Ball, Lewis & Thames (2008, p. 15) discuss this challenge for the elementary-grades teacher, who wants to give mathematical reasons for mathematical facts, but whose students neither use the same definition, nor would understand it if it were introduced.
- ^ Compare Lichtenberg (1972, p. 535) Fig. 1
- ^ Lichtenberg 1972, s. 535–536. "...numbers answer the question How many? for the set of objects ... zero is the number property of the empty set ... If the elements of each set are marked off in groups of two ... then the number of that set is an even number."
- ^ Lichtenberg 1972, s. 535–536. "Zero groups of two stars are circled. No stars are left. Therefore, zero is an even number."
- ^ Lichtenberg 1972, s. 537; compare her Fig. 3. "If the even numbers are identified in some special way ... there is no reason at all to omit zero from the pattern."
- ^ The Math Forum participants (2000). ”A question around zero” (på engelska). Math Forum » Discussions » History » Historia-Matematica. Drexel University. http://mathforum.org/kb/message.jspa?messageID=1178542. Läst 16 januari 2015.
- ^ Straight Dope Science Advisory Board (1999). ”Is zero odd or even?” (på engelska). The Straight Dope Mailbag. http://www.straightdope.com/columns/read/1723/is-zero-odd-or-even. Läst 16 januari 2015.
- ^ Doctor Rick (2001). ”Is Zero Even?” (på engelska). Ask Dr. Math. The Math Forum. http://mathforum.org/library/drmath/view/57188.html. Läst 16 januari 2015.
- ^ Grimes, Joseph E. (1975). The Thread of Discourse. Walter de Gruyter. ISBN 90-279-3164-X
- ^ Anthony Wilden, Rhonda Hammer (1987). The rules are no game: the strategy of communication. Routledge Kegan & Paul. sid. 104. ISBN 0-7100-9868-5
- ^ Snow, Tony (23 februari 2001). ”Bubba's fools” (på engelska). Jewish World Review. http://www.jewishworldreview.com/tony/snow022301.asp. Läst 16 januari 2015.
- ^ Morgan, Frank (5 april 2001). ”Old Coins” (på engelska). Frank Morgan's Math Chat. The Mathematical Association of America. Arkiverad från originalet den 8 januari 2009. https://web.archive.org/web/20090108053212/http://www.maa.org/features/mathchat/mathchat_4_5_01.html. Läst 16 januari 2015.
- ^ Steinberg, Neil (30 november 1999). ”Even år, odd facts”. ss. 50.
- ^ Siegel, Robert (19 november 1999). ”Analysis: Today's datum is signified in abbreviations using only odd numbers. 1-1, 1-9, 1-9-9-9” (på engelska). All Things Considered. National Public Radio. http://www.npr.org/templates/story/story.php?storyId=1066881. Läst 16 januari 2015.
- ^ Stingl, Jim (5 april 2006) (på engelska). 01:02:03 04/05/06; We can count on some things in life. sid. B1. Arkiverad från originalet den 27 april 2006. https://web.archive.org/web/20060427002610/http://www.jsonline.com/story/index.aspx?id=413306. Läst 16 januari 2015. Arkiverad 27 april 2006 hämtat från the Wayback Machine.
- ^ [a b] Bill Sones, Rich Sones (8 maj 2002). ”To hide your age, button your lips” (på engelska). Deseret News. sid. C07. http://www.deseretnews.com/article/912430/To-hide-your-age-button-your-lips.html?pg=all. Läst 16 januari 2015.
- ^ Kaplan Staff (2004) (på engelska). Kaplan SAT 2400, 2005 Edition. Simon and Schuster. ISBN 0-7432-6035-X
- ^ Arsham, Hossein (januari 2002) (på engelska). Zero in Four Dimensions: Historical, Psychological, Cultural, and Logical Perspectives. http://www.pantaneto.co.uk/issue5/arsham.htm. Läst 16 januari 2015 Arkiverad 25 september 2007 hämtat från the Wayback Machine.
- ^ Crumpacker, Bunny (2007). Perfect Figures: The Lore of Numbers and How We Learned to Count. Macmillan. sid. 165. ISBN 0-312-36005-3
- ^ Department of Legislative Reference (1974) (på engelska). Laws of the State of Maryland, Volume 2. https://books.google.se/books?id=nOhGAQAAIAAJ&q=%22ham+radio+operator+plates.+Zero+is+an+even+number%22&dq=%22ham+radio+operator+plates.+Zero+is+an+even+number%22&hl=sv&sa=X&ei=AEW5VMCJN8WZygPKrIHQBw&ved=0CCEQ6AEwAA. Läst 16 januari 2015
- ^ Cutler, Thomas J. (2008) (på engelska). The Bluejacket's Manual: United States Navy. Naval Institute Press. sid. 237-238. ISBN 1-55750-221-8
- ^ Brisman, Andrew (2004) (på engelska). Mensa Guide to Casino Gambling: Winning Ways. Sterling. sid. 153. ISBN 1-4027-1300-2
- ^ Smock, Doug (6 februari 2006). ”The odd bets: Hines Ward vs. Tiger Woods” (på engelska). ss. P1B.
- ^ Hohmann, George (25 oktober 2007). ”Companies let market determine new name” (på engelska). ss. P1C.
- ^ Turner, Julian (13 juli 1996). ”Sports Betting – For Lytham Look to the South Pacific” (på engelska). ss. 23.
- ^ Diagram Group (1983) (på engelska). The Official World Encyclopedia of Sports and Games. Paddington Press. sid. 213. ISBN 0-448-22202-7
Externa länkar
[redigera | redigera wikitext] Wikimedia Commons har media som rör Paritet av noll.
Wikimedia Commons har media som rör Paritet av noll. Wiktionary har ett uppslag om noll.
Wiktionary har ett uppslag om noll.
- Is Zero Even? - Numberphile, En film med Dr. James Grime, University of Nottingham (engelska)