Matrika razdalj

Matrika razdalj je matrika, ki vsebuje razdalje med posameznimi elementi množice. Matrika ima razsežnost $n\times n\,$ , kjer je $n\,$ število elementov množice, oziroma število vozlišč, če se hoče prikazati graf. Razdalje med vozlišči se lahko meri v poljubnih enotah za merjenje razdalj.

Zgleda

1. zgled

Včasih matrika razdalj opisuje tudi število povezav med dvema vozliščema. To je zelo primerno za prikazovanje števila povezav med atomi v molekuli.

To se lahko prikaže kot matriko razdalj.

{\begin{bmatrix}0&1&2&3&4&5&3&4\\1&0&1&2&3&4&2&3\\2&1&0&1&2&3&1&2\\3&2&1&0&1&2&2&3\\4&3&2&1&0&1&3&4\\5&4&3&2&1&0&4&5\\3&2&1&2&3&4&0&1\\4&3&2&3&4&5&1&0\end{bmatrix}}

.

Matrika razdalj je simetrična.

2. zgled

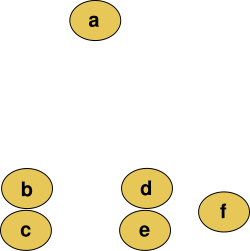
V tem zgledu pa so razdalje prikazane kot število pikslov, ki pripadajo posameznim razdaljam med točkami. Pripadajočo matriko razdalj se lahko prikaže kot

	a	b	c	d	e	f
a	0	184	222	177	216	231
b	184	0	45	123	128	200
c	222	45	0	129	121	203
d	177	123	129	0	46	83
e	216	128	121	46	0	83
f	231	200	203	83	83	0

kjer so v prvi vrstici in prvem stolpcu naštete točke. V matriki pa so podane razdalje med njimi v pikslih.

Primerjava z drugimi matrikami

Matrika razdalj je sorodna matriki sosednosti. Od nje se razlikuje v tem, da matrika sosednosti prikazuje samo povezave, ne prikazuje pa razdalj med vozlišči. Druga razlika je v tem, da je v matriki razdalj, manjša razdalja med vozlišči tudi prikazana kot manjša.

V nasprotju z matriko evklidskih razdalj matrika razdalj ni vedno simetrična

Glej tudi

Zunanje povezave

Weisstein, Eric Wolfgang. »Graph Distance Matrix«. MathWorld.