Шар

Шар — геометрическое тело; совокупность всех точек пространства, находящихся от центра на расстоянии, не больше заданного. Это расстояние называется радиусом шара. Шар образуется вращением полукруга (или круга) вокруг его неподвижного диаметра. Этот диаметр называется осью шара, а оба конца указанного диаметра — полюсами шара. Поверхность шара называется сферой: замкнутый шар включает эту сферу, открытый шар — исключает.

Шар

Поверхность шара — сфера
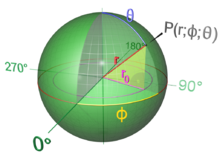
r — радиус шара

Связанные определения

Если секущая плоскость проходит через центр шара, то сечение шара называется большим кругом. Другие плоские сечения шара называются малыми кругами. Площадь этих сечений вычисляется по формуле πR².

Основные геометрические формулы

Площадь поверхности $S$ и объём $V$ шара радиуса $r$ (и диаметром $d=2r$) определяются формулами:

• $S=\ 4\pi r^{2}$

  $S=\ \pi d^{2}$

  $V={\frac {4}{3}}\pi r^{3}$

Доказательство

Возьмём четверть круга радиуса R с центром в точке $\left(0;0\right)$. Уравнение окружности этого круга : $x^{2}+y^{2}=R^{2}$, откуда $y^{2}=R^{2}-x^{2}$.

Функция $y={\sqrt {R^{2}-x^{2}}},x\in (0;R)$ непрерывная, убывающая, неотрицательная. При вращении четверти круга вокруг оси Ox образуется полушар, следовательно:

${1 \over 2}V=\pi \int \limits _{0}^{R}(R^{2}-x^{2})dx=\pi \cdot {\Bigl .}\left(R^{2}x-{\frac {x^{3}}{3}}\right){\Bigr |}_{0}^{R}=\pi \cdot (R^{3}-{\frac {R^{3}}{3}})={\frac {2}{3}}\pi R^{3}$

Откуда $V={\frac {4}{3}}\pi R^{3}$ Ч. т. д.

• $V={\frac {\pi d^{3}}{6}}$

Доказательство

$d=2r,V={4 \over 3}\pi r^{3}={4 \over 3}\pi \left({d \over 2}\right)^{3}={4 \over 3}\pi {\frac {d^{3}}{8}}={\frac {\pi d^{3}}{6}}$ Ч. т. д.

Понятие шара в метрическом пространстве естественно обобщает понятие шара в евклидовой геометрии.

Определения

Пусть дано метрическое пространство $(X,\rho )$. Тогда

• Шаром (или открытым шаром) с центром в точке $x_{0}\in X$ и радиусом $r>0$ называется множество

$B_{r}(x_{0})=\{x\in X\mid \rho (x,x_{0})<r\}.$

• Замкнутым шаром с центром в $x_{0}$ и радиусом $r$ называется множество

$D_{r}(x_{0})=\{x\in X\mid \rho (x,x_{0})\leqslant r\}.$

Замечания

Шар радиуса $r$ с центром $x_{0}$ также называют $r$-окрестностью точки $x_{0}$.

Свойства

• Шар является открытым множеством в топологии, порождённой метрикой $\rho$.
• Замкнутый шар — замкнутым множеством в топологии, порождённой метрикой $\rho$.
• По определению такой топологии открытые шары с центрами в любой точке $X$ являют собой её базу.
• Очевидно, $B_{r}(x_{0})\subset D_{r}(x_{0})$. Однако, вообще говоря, замыкание открытого шара может не совпадать с замкнутым шаром: ${\overline {B_{r}(x_{0})}}\neq D_{r}(x_{0}).$
  • Например: пусть $(X,\rho )$ — дискретное метрическое пространство, и $X$ состоит из более, чем двух точек. Тогда для любого $x\in X$ имеем:

$B_{1}(x)=\{x\},\;{\overline {B_{1}(x)}}=\{x\},\;D_{1}(x)=X.$

Объём

Объём n-мерного шара радиуса R в n-мерном евклидовом пространстве:

$V_{n}(R)={\frac {\pi ^{n/2}}{\Gamma ({\frac {n}{2}}+1)}}R^{n},$

где Γ — это эйлеровская гамма-функция (которая является расширением факториала на поле действительных и комплексных чисел). Используя частные представления гамма-функции для целых и полуцелых значений, можно получить формулы объёма n-мерного шара, которые не требуют гамма-функции:

$V_{2k}(R)={\frac {\pi ^{k}}{k!}}R^{2k}$,

$V_{2k+1}(R)={\frac {2^{k+1}\pi ^{k}}{(2k+1)!!}}R^{2k+1}={\frac {2(k!)(4\pi )^{k}}{(2k+1)!}}R^{2k+1}$.

Знаком !! здесь обозначен двойной факториал.

Эти формулы также можно свести в одну общую:

$V_{n}(R)={\frac {2^{\left[{\frac {n+1}{2}}\right]}\pi ^{\left[{\frac {n}{2}}\right]}}{n!!}}R^{n}$.

Обратная функция для выражения зависимости радиуса от объёма:

$R_{n}(V)={\frac {\Gamma (n/2+1)^{1/n}}{\sqrt {\pi }}}V^{1/n}$.

Эта формула также может быть разделена на две: для пространств с чётным и нечётным количеством размерностей, используя факториал и двойной факториал вместо гамма-функции:

$R_{2k}(V)={\frac {(k!V)^{1/2k}}{\sqrt {\pi }}}$,

$R_{2k+1}(V)=\left({\frac {(2k+1)!!V}{2^{k+1}\pi ^{k}}}\right)^{1/(2k+1)}$.

Рекурсия

Формулу объёма также можно выразить в виде рекурсивной функции. Эти формулы могут быть доказаны непосредственно или выведены из основной формулы, представленной выше. Проще всего выразить объём n-мерного шара через объём шара размерности $n-2$ (при условии, что они имеют одинаковый радиус):

$V_{n}(R)={\frac {2\pi R^{2}}{n}}V_{n-2}(R)$.

Также существует формула объёма n-мерного шара в зависимости от объёма (n−1)-мерного шара того же радиуса:

$V_{n}(R)=R{\sqrt {\pi }}{\frac {\Gamma ({\frac {n+1}{2}})}{\Gamma ({\frac {n}{2}}+1)}}V_{n-1}(R)$.

То же без гамма-функции:

${\begin{aligned}V_{2k}(R)&=R\pi {\frac {(2k-1)!!}{2^{k}k!}}V_{2k-1}(R)=R\pi {\frac {(2k-1)(2k-3)\cdots 5\cdot 3\cdot 1}{(2k)(2k-2)\cdots 6\cdot 4\cdot 2}}V_{2k-1}(R),\\V_{2k+1}(R)&=2R{\frac {2^{k}k!}{(2k+1)!!}}V_{2k}(R)=2R{\frac {(2k)(2k-2)\cdots 6\cdot 4\cdot 2}{(2k+1)(2k-1)\cdots 5\cdot 3\cdot 1}}V_{2k}(R).\end{aligned}}$

Пространства младших размерностей

Формулы объёма для некоторых пространств младших размерностей:

Кол-во измерений	Объём шара радиуса R	Радиус шара объёма V
1	$2R$	$V/2$
2	$\pi R^{2}$	${\frac {V^{1/2}}{\sqrt {\pi }}}$
3	${\frac {4\pi }{3}}R^{3}$	$\left({\frac {3V}{4\pi }}\right)^{1/3}$
4	${\frac {\pi ^{2}}{2}}R^{4}$	${\frac {(2V)^{1/4}}{\sqrt {\pi }}}$
5	${\frac {8\pi ^{2}}{15}}R^{5}$	$\left({\frac {15V}{8\pi ^{2}}}\right)^{1/5}$
6	${\frac {\pi ^{3}}{6}}R^{6}$	${\frac {(6V)^{1/6}}{\sqrt {\pi }}}$
7	${\frac {16\pi ^{3}}{105}}R^{7}$	$\left({\frac {105V}{16\pi ^{3}}}\right)^{1/7}$
8	${\frac {\pi ^{4}}{24}}R^{8}$	${\frac {(24V)^{1/8}}{\sqrt {\pi }}}$
9	${\frac {32\pi ^{4}}{945}}R^{9}$	$\left({\frac {945V}{32\pi ^{4}}}\right)^{1/9}$
10	${\frac {\pi ^{5}}{120}}R^{10}$	${\frac {(120V)^{1/10}}{\sqrt {\pi }}}$

Пространства старших размерностей

Объём гипершара размерности n единичного радиуса в зависимости от n.

При стремлении количества размерностей к бесконечности объём шара единичного радиуса стремится к нулю. Это может быть выведено из рекурсивного представления формулы объёма.

Примеры

• Пусть $\mathbb {R} ^{d}$ — евклидово пространство с обычным евклидовым расстоянием. Тогда

• если $d=1$ (пространство — прямая), то

$B_{r}(x_{0})=\{x\in \mathbb {R} \mid |x-x_{0}|<r\}=\left(x_{0}-{r},x_{0}+{r}\right),$

$D_{r}(x_{0})=\{x\in \mathbb {R} \mid |x-x_{0}|\leq r\}=\left[x_{0}-{r},x_{0}+{r}\right].$

 — открытый и замкнутый отрезок соответственно.

• если $d=2$ (пространство — плоскость), то

  $B_{r}((x_{0},y_{0}))=\left\{(x,y)\in \mathbb {R} ^{2}\mid {\sqrt {(x-x_{0})^{2}+(y-y_{0})^{2}}}<r\right\},$

  $D_{r}((x_{0},y_{0}))=\left\{(x,y)\in \mathbb {R} ^{2}\mid {\sqrt {(x-x_{0})^{2}+(y-y_{0})^{2}}}\leq r\right\}$

 — открытый и замкнутый диск соответственно.

• если $d=3$, то

  $B_{r}((x_{0},y_{0},z_{0}))=\left\{(x,y,z)\in \mathbb {R} ^{3}\mid {\sqrt {(x-x_{0})^{2}+(y-y_{0})^{2}+(z-z_{0})^{2}}}<r\right\},$

  $D_{r}((x_{0},y_{0},z_{0}))=\left\{(x,y,z)\in \mathbb {R} ^{3}\mid {\sqrt {(x-x_{0})^{2}+(y-y_{0})^{2}+(z-z_{0})^{2}}}\leq r\right\}$

 — открытый и замкнутый стереометрический шар соответственно.

• В иных метриках шар может иметь иную геометрическую форму. Например, определим в евклидовом пространстве $\mathbb {R} ^{d}$ метрику следующим образом:

  $\rho (x,y)=\sum \limits _{i=1}^{d}\|x_{i}-y_{i}\|,\quad x=(x_{1},\ldots ,x_{d})^{\top },y=(y_{1},\ldots ,y_{d})^{\top }\in \mathbb {R} ^{d}.$

Тогда

• если $d=2$, то $U_{r}(x_{0})$ — это открытый квадрат с центром в точке $x_{0}$ и сторонами длины ${\sqrt {2}}$, расположенными по диагонали к координатным осям.
• если $d=3$, то $U_{r}(x_{0})$ — это открытый трёхмерный октаэдр.

См. также

• Шаровой слой
• Гиперсфера
• Сферический слой

Литература

• Шар, геометрическое тело // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). — СПб., 1890—1907.

Ссылки на онлайн калькуляторы

• Вычисление объема и площади шара  (неопр.). Дата обращения: 12 марта 2012. Архивировано из оригинала 8 августа 2011 года.
• Онлайн-калькуляторы  (неопр.). Дата обращения: 2 июля 2019. Архивировано из оригинала 9 января 2019 года.
• Математические этюды  (неопр.). Дата обращения: 20 октября 2011. Архивировано из оригинала 18 октября 2011 года. Мультфильм про объём шара