Endecagramă
| Endecagramă regulată | |
 Cele patru stelări ale endecagonului regulat | |
| Tip | figură poligonală regulată |
|---|---|
| Laturi și vârfuri | 11 |
| Simbol Schläfli | {11/2}, {11/3}, {11/4}, {11/5} |
| Diagramă Coxeter | |
| Grup de simetrie | Diedrală (D11), ordin 22 |
| Unghi interior (grade) | ≈114,545° {11/2} ≈81,8182° {11/3} ≈49,0909° {11/4} ≈16,3636° {11/5} |
| Proprietăți | poligon stelat, echilateral, izogonal, izotoxal |
În geometrie o endecagramă este un poligon stelat cu unsprezece vârfuri,[1] cu simbolurile Schläfli {11/2}, {11/3}, {11/4}, respectiv {11/5}.
Denumirea endecagramă combină prefixul numeric endeca-[2] cu sufixul -gramă, care derivă din greacă γραμμῆ, care înseamnă o dreaptă.[3]
Endecagrame regulate
[modificare | modificare sursă]Există patru endecagrame regulate,[4] care pot fi descrise de simbolurile Schläfli {11/2} (mica endecagramă), {11/3} (endecagramă [mediană]), {11/4} (marea endecagramă), respectiv {11/5} (larga endecagramă), în care primul număr este numărul vârfurilor, iar cel de după bara oblică este pasul stelării endecagonului regulat.[5]
Deoarece 11 este un număr prim, toate endecagramele sunt poligoane stelate, nu compuși poligonali.
Construcție
[modificare | modificare sursă]Ca și în cazul tuturor poligoanelor regulate cu un număr impar de laturi și poligoanelor stelate ale căror ordin nu sunt produse de numere Fermat prime distincte, endecagramele regulate nu pot fi construite cu rigla și compasul.[6] Totuși, există metode de a construi endecagramele {11/3}, {11/4} și {11/5} din benzi de hârtie împăturite.[7]
Aplicații
[modificare | modificare sursă]Prismele endecagramice {11/3} și {11/4} pot fi folosite pentru a aproxima forma moleculelor de ADN.[8]

Sulul Topkapı conține imagini ale unei stele girih cu 11 colțuri, folosită în arta islamică. Steaua din acest sul nu este una dintre formele obișnuite ale endecagramei, ci folosește drepte care leagă vârfurile unui endecagon cu punctele din mijloacele laturilor aproape opuse ale endecagonului.[9] Steaua girih cu 11 colțuri se regăsește pe exteriorul Mausoleului Momine Khatun (în română Mausoleul Doamnei Momine). Eric Broug scrie că acest model „poate fi considerat un punct culminant în desenul geometric islamic”.[10]
Camera de ardere (spațiul gol) de la propulsoarele cu combustibil solid ale navetelor spațiale americane avea o secțiune în formă de stea cu 11 colțuri. Această formă a oferit o suprafață mai mare și o tracțiune mai mare la începutul lansării și o rată de ardere mai lentă, respectiv o tracțiune mai mică după ce părțile stelei dinspre mijloc au fost arse, aproximativ după ce naveta a trecut de bariera sunetului.[11]
Poliedre endecagramice
[modificare | modificare sursă]Pe baza celor patru endecagrame se pot construi prismele, antiprismele și retroprismele endecagramice corespunzătoare.
 Prismă 11-2 |
 Prismă 11-3 |
 Prismă 11-4 |
 Prismă 11-5 |
 Antiprismă 11-2 |
 Antiprismă 11-3 |
 Antiprismă 11-4 |
 Antiprismă 11-5 |
 Retroprismă 11-7 |
 Retroprismă 11-6 |
Note
[modificare | modificare sursă]- ^ en „Between a square rock and a hard pentagon: Fractional polygons”. .
- ^ „endeca” la DEX online
- ^ en Liddell, Henry George; Scott, Robert (), A Greek-English Lexicon: γραμμή, Oxford: Clarendon Press
- ^ en O'Daffer, Phares G.; Clemens, Stanley R. (), Geometry: an investigative approach
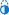 , Addison-Wesley, Exercise 7, p. 62, ISBN 9780201054200
, Addison-Wesley, Exercise 7, p. 62, ISBN 9780201054200
- ^ en Agricola, Ilka; Friedrich, Thomas (), Elementary Geometry, Student mathematical library, 43, American Mathematical Society, p. 96, ISBN 9780821890677
- ^ en Carstensen, Celine; Fine, Benjamin; Rosenberger, Gerhard (), Abstract Algebra: Applications to Galois Theory, Algebraic Geometry, and Cryptography, Sigma series in pure mathematics, 11, Walter de Gruyter, p. 88, ISBN 9783110250084,
On the other hand a regular 11-gon is not constructible.
- ^ en Hilton, Peter; Pedersen, Jean (), „Symmetry in mathematics”, Computers & Mathematics with Applications, 12 (1-2): 315–328, doi:10.1016/0898-1221(86)90157-4, MR 0838152
- ^ en Janner, Aloysio (iunie 2001), „DNA enclosing forms from scaled growth forms of snow crystals”, Crystal Engineering, 4 (2–3): 119–129, doi:10.1016/S1463-0184(01)00005-3
- ^ en Bodner, B. Lynn (), „The eleven–pointed star polygon design of the Topkapı Scroll”, Bridges 2009: Mathematics, Music, Art, Architecture, Culture (PDF), pp. 147–154
- ^ en Broug, Eric (), Islamic Geometric Design, Thames & Hudson, p. 182
- ^ en Angelo, Joseph A. (), Encyclopedia of Space and Astronomy, Infobase Publishing, p. 511, ISBN 9781438110189
Bibliografie
[modificare | modificare sursă]- en John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, The Symmetries of Things 2008, ISBN: 978-1-56881-220-5 (Chapter 26. pp. 404: Regular star-polytopes Dimension 2)