Epicykel

Epicykels zijn hulpcirkels, meestal bedoeld om de schijnbare bewegingen van de planeten aan het hemelgewelf te kunnen verklaren.

Door de epicykel wordt een retrograde planeetbeweging gesimuleerd. Dit model is té eenvoudig: de lussen die de astronoom meet zijn niet alle even groot

Basiselementen van het Ptolemaeïsch systeem

Deze hulpcirkels zijn bedacht door Apollonios van Pergē (ca. 200 v.Chr.), en werden overgenomen door latere astronomen zoals Claudius Ptolemaeus. In zijn tijd ging men ervan uit dat de aarde in het middelpunt van het zonnestelsel stond, en dat de zon, maan en planeten eromheen draaiden. Naar het model van de Aristotelische wetenschappen, waaraan de Kerk zijn uitgangspunten over wetenschap heeft ontleend, moesten alle banen in het bovenmaanse perfect zijn: cirkelvormig. Men kon met zuiver cirkelvormige banen de beweging van de planeten aan het firmament niet verklaren.

Een eerste probleem was de soms retrograde (schijnbaar terugwaartse) beweging van de planeten (lussen). Dit probleem kon worden opgelost met een enkele epicykel die dezelfde middellijn heeft als de baan van de zon om de aarde. De planeten zouden in een perfecte cirkel om het middelpunt van een epicykel draaien. Het middelpunt van die epicykel beweegt zich op een grotere cirkelbaan met constante snelheid (eenparig). Deze denkbeeldige baan werd de deferent genoemd.

Na deze verbetering doet zich een tweede probleem voor: men observeert dat de lussen van de epicykels niet even groot zijn (zoals in het eerste diagram; té eenvoudig dus) en dat de gemeten snelheid van de planeten onregelmatig is: Ptolemaeus plaatste daarom de aarde opzij van het middelpunt van de deferent (zie figuur; het middelpunt is een kruisje) en berekende de snelheid van het middelpunt van de epicykel niet meer constant (eenparig) om het middelpunt, maar eenparig om de equant (of vereffeningspunt (het zwarte punt), aan de andere kant van het middelpunt). Hierdoor werden de planeetbanen beter voorspelbaar: de variabele snelheid en de onregelmatige groottes van de lussen waren opgelost. De ingrediënten van het model zijn dan: een middelpunt, aan weerszijden een aardpositie en een equant, een deferent en een epicykel; een berekening kan Ptolemaeus dan maken door op een begintijdstip een startpunt op de deferent en op de epicykel te kennen, en door daaraan de hoeksnelheid op de epicykel (eenvoudig: een volle cirkel per jaar) en de hoeksnelheid vanuit de equant (afhankelijk van de planeet), beide vermenigvuldigd met de tijd sinds het begintijdstip toe te voegen. De berekening kon gebeuren met Ptolemaeus' tabellen, en met een "analoge rekenmachine" (een "volvelle"). Het resultaat is een coördinaat op de ecliptica (bv. 8 graden in Saggitarius), afleesbaar met een touwtje op de buitenste cirkel.

Een volvelle, samengesteld uit papieren schijven en touwtjes, dat op eenvoudige manier de positie van Mars (planeet) met de methode van Ptolemaeus laat berekenen. Uit Astronomicum Caesareum van Petrus Apianus uit 1540.

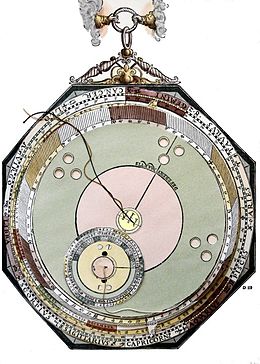
De epicykels zijn even groot als de baan van de zon om de aarde. Bovendien is de omloop in de epicykels synchroon met de zon.

Zo kon de schijnbare beweging van de planeten aan de hemel worden verklaard, inclusief de lusvorming die inhoudt dat een planeet schijnbaar achterwaarts beweegt.

Toen Nicolaus Copernicus een ander model maakte van het zonnestelsel (zie Heliocentrische theorie), met daarin de zon in het middelpunt, had hij de eerste epicykel niet meer nodig. Hij ging echter nog steeds uit van perfect cirkelvormige banen: daardoor waren tientallen epicykels nodig om correcties aan te brengen.

Pas toen Johannes Kepler met zijn drie Wetten van Kepler definitief met de perfect cirkelvormige banen afrekende en elliptische banen voorstelde, kon eens en voor altijd worden afgerekend met de epicykels. Deze "nekslag" voor het model van Ptolemaeus brengt ook de genialiteit van het ptolemaeïsch model aan het licht: door de aarde in een punt opzij van de deferent te plaatsen, en de eenparige snelheid van de planeet vanuit het vereffeningspunt aan te drijven, had hij in feite een ellips gesimuleerd (aarde en equant zijn de brandpunten van die ellips)) - zonder te moeten toegeven dat het om een ellips ging. Door deze "stiekeme" ellips was het Ptolemaeïsch model ook ná Copernicus (die perfecte cirkels postuleerde, en strijdig was met de toenmalige fysica en observaties) voor de astronomen nog steeds een beter model.

Externe link

• Animatie van epicykels met instelbare parameters en voorgeconfigureerde parameters van een aantal planeten (Engels) (nota: om te visualiseren dat de lussen van de epicykels niet altijd even groot zijn, moet men "path duration" op maximum instellen; stel ook de eccentriciteit (de "ellipsvorm") maximaal in om het effect te zien).

Bronnen, noten en/of referenties