Shape that a bending rod makes

Question

I recently found that a rope suspended from two points forms the shape of a catenary curve, which brought me to another question:

What is the shape made by a rod of uniform density when only one of its ends is held horizontally?

Obviously the material and width would affect the strength of the rod and thus the shape it makes, however I assume they must all resemble the same curve. (similar to how all shapes and sizes of ropes will resemble a catenary curve when held at two points)

I would love any help with this question!

Answer 1

There is a whole theory for this, namely the Euler–Bernoulli beam theory. The Wikipedia page is very rich.

To summarize it very roughly, if you call $w(x)$ the vertical displacement of the beam at position $x$, then $w$ satisfies the (static) differential equation: $$ EI \frac{\mathrm{d}^4 w}{\mathrm{d}x^4} (x) = q(x), $$ where $EI$ is a constant, the flexural rigidity, and $q(x)$ denotes the load at point $x$. You then have to supplement this fourth-order differential equation with 4 boundary conditions. A typical setting is to have a fixed end at $x = 0$, which corresponds to $w(0) = w'(0) = 0$ and a free end at $x = L$ which corresponds to $w''(L) = w'''(L) = 0$.

You can compute explicit solutions in many cases. A very important feature is the maximal displacement at the endpoint. For example for the above boundary conditions (called cantilever beam) and with a uniform load, it is given by $$ w(L) = \frac{q}{8EI} L^4, $$ which scales like $L^4$, giving a solid ground to the intuition that $w(L)$ increases very rapidly with $L$.

Answer 2

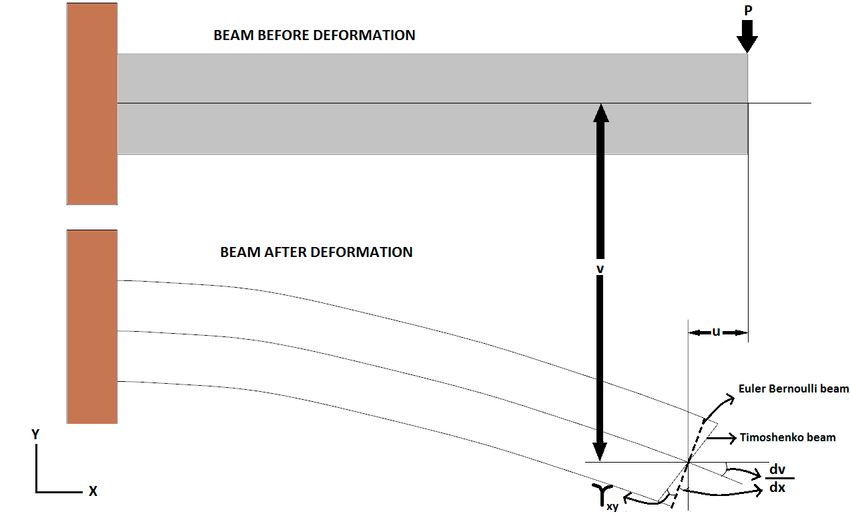
When the rod is thick Euler's theory fails to decribe properly the deformation, in these case we refer to Timoshenko beam theory. In this case, the governing equations are the following coupled system of ordinary differential equations:

$$ \frac{d^2}{d x^2}\left(EI\frac{d \varphi}{d x}\right) = q(x) \\ \frac{d w}{d x} = \varphi - \frac{1}{\kappa AG} \frac{d}{d x}\left(EI\frac{d \varphi}{d x}\right) $$

where

• $L$ is the length of the beam.
• $A$ is the cross section area.
• $E$ is the elastic modulus.
• $G$ is the shear modulus.
• $I$ is the second moment of area.
• $\kappa$, called the Timoshenko shear coefficient, depends on the geometry ($\kappa = 5/6$ for a rectangular section).
• $q(x)$ is a distributed load (force per length).

Timoshenko beam theory for the static case is equivalent to the Euler–Bernoulli beam theory when the last term above is neglected, an approximation that is valid when $\frac{3EI}{\kappa L^2 A G} \ll 1$, that is when the beam is sufficiently slender.

Combining the two equations gives, for a homogeneous beam of constant cross-section, the differential equation

$$ EI\frac{d^4 w}{d x^4} = q(x) - \frac{EI}{\kappa A G}\frac{d^2 q}{d x^2}$$

which leads to a different shape and a larger deflection with respect to the approximate Euler's theory.

(credits)