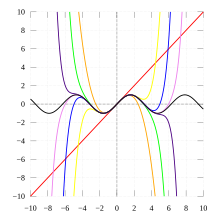
사인 함수 와 그 테일러 다항식 들은 모두 홀함수이다. 그림은 사인 함수와 그 1, 3, 5, 7, 9, 11, 13차 테일러 다항식의 그래프.코사인 함수 와 그 테일러 다항식들은 모두 짝함수이다. 그림은 코사인 함수와 그 4차 테일러 다항식의 그래프.수학 에서 홀함수 (영어 : odd function ) 또는 기함수 (奇函數)는 서로 덧셈 역원 의 상이 서로 덧셈 역원인 실수 함수 이다. 짝함수 (영어 : even function ) 또는 우함수 (偶函數)는 서로 덧셈 역원의 상이 서로 같은 실수 함수이다. 해석학 의 테일러 급수 와 푸리에 급수 이론에서 중요하게 사용되는 개념이다. 멱함수 의 홀짝성이 그 지수의 홀짝성과 일치한다는 데에서 이름을 따왔다.
실수 함수
f
:
D
→
R
{\displaystyle f\colon D\to \mathbb {R} }
D
⊆
R
{\displaystyle D\subseteq \mathbb {R} }
−
D
=
D
{\displaystyle -D=D}
구간 이라고 하자.
만약 임의의
x
∈
D
{\displaystyle x\in D}
f
(
−
x
)
=
−
f
(
x
)
{\displaystyle f(-x)=-f(x)}
f
{\displaystyle f}
홀함수 라고 한다.
만약 임의의
x
∈
D
{\displaystyle x\in D}
f
(
−
x
)
=
f
(
x
)
{\displaystyle f(-x)=f(x)}
f
{\displaystyle f}
짝함수 라고 한다. 홀함수이자 짝함수는 영함수밖에 없다. 이는 항상
f
(
x
)
=
(
f
(
−
x
)
+
(
−
f
(
−
x
)
)
)
/
2
=
0
{\displaystyle f(x)=(f(-x)+(-f(-x)))/2=0}
홀함수도 짝함수도 아닌 함수는 존재한다. 예를 들어,
f
(
x
)
=
x
+
1
{\displaystyle f(x)=x+1}
f
(
−
1
)
=
0
≠
±
2
=
±
f
(
1
)
{\displaystyle f(-1)=0\neq \pm 2=\pm f(1)}
홀함수는 다음과 같은 꼴의 함수와 동치 이다.
x
f
(
x
2
)
(
f
:
D
→
R
)
{\displaystyle xf(x^{2})\qquad (f\colon D\to \mathbb {R} )}
짝함수는 다음과 같은 꼴의 함수와 동치이다.
f
(
x
2
)
(
f
:
D
→
R
)
{\displaystyle f(x^{2})\qquad (f\colon D\to \mathbb {R} )}
함수는 항상 짝함수와 홀함수의 합으로 유일하게 나타낼 수 있다. 이는 다음과 같다.
f
(
x
)
=
f
(
x
)
+
f
(
−
x
)
2
+
f
(
x
)
−
f
(
−
x
)
2
{\displaystyle f(x)={\frac {f(x)+f(-x)}{2}}+{\frac {f(x)-f(-x)}{2}}}
짝함수
R
→
R
{\displaystyle \mathbb {R} \to \mathbb {R} }
R
{\displaystyle \mathbb {R} }
대수 를 이루며, 홀함수
R
→
R
{\displaystyle \mathbb {R} \to \mathbb {R} }
R
{\displaystyle \mathbb {R} }
벡터 공간 을 이룬다. 함수
R
→
R
{\displaystyle \mathbb {R} \to \mathbb {R} }
직합 이다.
R
R
=
{
f
∈
R
R
:
f
(
−
x
)
=
f
(
x
)
}
⊕
{
f
∈
R
R
:
f
(
−
x
)
=
−
f
(
x
)
}
{\displaystyle \mathbb {R} ^{\mathbb {R} }=\{f\in \mathbb {R} ^{\mathbb {R} }\colon f(-x)=f(x)\}\oplus \{f\in \mathbb {R} ^{\mathbb {R} }\colon f(-x)=-f(x)\}}
홀짝성이 주어진 함수의 사칙 연산의 홀짝성에 대하여, 다음 성질들이 성립한다.
홀함수와 홀함수의 합·차는 홀함수이다.
짝함수와 짝함수의 합·차는 짝함수이다.
영이 아닌 홀함수와 영이 아닌 짝함수의 합·차는 홀함수도 짝함수도 아니다.
홀함수와 홀함수의 곱·몫은 짝함수이다.
홀함수와 짝함수의 곱·몫은 홀함수이다. 특히, 홀함수의 상수곱은 홀함수이다.
짝함수와 짝함수의 곱·몫은 짝함수이다. 특히, 짝함수의 상수곱은 짝함수이다. 미분 가능 함수 의 경우, 다음 성질들이 성립한다.
홀함수의 미분 은 짝함수이다.
짝함수의 미분은 홀함수이다. 어떤 함수가 짝함수의 필요 충분 조건은, 그래프 가
y
{\displaystyle y}
어떤 함수가 홀함수일 필요 충분 조건은, 그래프가 원점에 대하여 대칭인 것이다.
홀함수
f
:
[
−
a
,
a
]
→
R
{\displaystyle f\colon [-a,a]\to \mathbb {R} }
적분 은 다음과 같다.
∫
−
a
a
f
(
x
)
d
x
=
0
{\displaystyle \int _{-a}^{a}f(x)\mathrm {d} x=0}
짝함수
f
:
[
−
a
,
a
]
→
R
{\displaystyle f\colon [-a,a]\to \mathbb {R} }
∫
−
a
a
f
(
x
)
d
x
=
2
∫
0
a
f
(
x
)
d
x
{\displaystyle \int _{-a}^{a}f(x)\mathrm {d} x=2\int _{0}^{a}f(x)\mathrm {d} x}
짝함수의 매클로린 급수 는 차수가 짝수인 항으로만 구성된다. 홀함수의 테일러 급수는 차수가 홀수인 항으로만 구성된다.
짝 주기 함수 의 푸리에 급수 는 코사인 항으로만 구성된다. 즉, 다음과 같은 꼴이다.
f
(
x
)
=
a
0
+
∑
n
=
1
∞
a
n
cos
2
n
π
T
x
{\displaystyle f(x)=a_{0}+\sum \limits _{n=1}^{\infty }{a_{n}\cos {\frac {2n\pi }{T}}x}}
홀 주기 함수의 푸리에 급수는 사인 항으로만 구성된다. 즉, 다음과 같은 꼴이다.
f
(
x
)
=
∑
n
=
1
∞
b
n
sin
2
n
π
T
x
{\displaystyle f\left(x\right)=\sum \limits _{n=1}^{\infty }{b_{n}\sin {\frac {2n\pi }{T}}x}}
함수
f
(
x
)
=
x
2
{\displaystyle f(x)=x^{2}}
함수
f
(
x
)
=
x
3
{\displaystyle f(x)=x^{3}}
함수
f
(
x
)
=
x
3
+
1
{\displaystyle f(x)=x^{3}+1}
홀함수의 몇 가지 예는 다음과 같다.
(항등 함수 )
x
{\displaystyle x}
(홀수차 멱함수)
x
3
{\displaystyle x^{3}}
(사인 )
sin
x
{\displaystyle \sin x}
(쌍곡선 사인 )
sinh
x
{\displaystyle \sinh x}
(오차 함수 )
erf
x
{\displaystyle \operatorname {erf} x}
짝함수의 몇 가지 예는 다음과 같다.
(상수 함수 )
c
{\displaystyle c}
(짝수차 멱함수)
x
2
{\displaystyle x^{2}}
(절댓값 )
|
x
|
{\displaystyle |x|}
(코사인 )
cos
x
{\displaystyle \cos x}
(쌍곡선 코사인 )
cosh
x
{\displaystyle \cosh x}
(가우스 곡선 )
exp
(
−
x
2
/
2
)
{\displaystyle \exp(-x^{2}/2)}