Gerarchia di massa dei neutrini
La gerarchia di massa dei neutrini si riferisce al modo in cui sono ordinate le masse dei neutrini in funzione della loro generazione. I quark e i leptoni carichi (elettrone, muone e tau) sono a massa crescente al crescere della loro generazione, vale a dire che i quark up e down, di prima generazione, sono più leggeri dei quark charm e strange, di seconda generazione, che a loro volta sono più leggeri dei quark top e bottom, di terza generazione. Lo stesso per l'elettrone, prima generazione, il muone, seconda generazione, e il tau, terza generazione.
Le masse dei neutrini non sono state ancora misurate ed in linea di principio possono non seguire l'ordinamento degli altri fermioni del modello standard.
Storia
[modifica | modifica wikitesto]La scoperta delle oscillazioni di neutrini è stata premiata con il Premio Nobel per la Fisica 2015 "per la scoperta dell'oscillazione dei neutrini, che dimostra che il Neutrino ha massa".[1][2]
Le oscillazioni dei neutrini possono avvenire solo se la massa dei neutrini è maggiore di zero, ma non sono in grado di dare informazioni sui valori delle masse, perché dipendono dalle differenze dei quadrati delle masse , con ma non dai valori delle singole masse mi.
La misura della massa dei neutrini rimane uno dei temi principali della fisica delle alte energie[3], e può essere ottenuta con misure dirette come studi dettagliati dello spettro dei decadimenti beta e la ricerca dei doppi decadimenti beta senza neutrini o con misure cosmologiche. Nessuno di questi approcci è stato finora in grado di misurare le masse dei neutrini, e al momento sono stati ottenuti solo limiti superiori ai valori delle masse.[4]
Descrizione
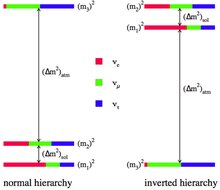
[modifica | modifica wikitesto]Il fatto che gli autostati di "sapore" dei neutrini, (neutrino elettronico, muonico e tauonico rispettivamente) siano mescolati agli autostati di massa attraverso le oscillazioni di neutrini, fa in modo che una misura di massa diretta si riferisca ad una particolare combinazione delle tre masse m1, m2, m3, relative ai tre autostati di massa . Ad esempio i decadimenti doppio beta senza neutrini misurano la combinazione , dove θ12 e θ13 sono due angoli di mixing misurati dalle oscillazioni di neutrini e α1 e α2 sono due fasi caratteristiche dei neutrini di Majorana. Nella formula compare una ulteriore indeterminazione, legata al fatto che la massa m1 può essere la più leggera o la più pesante delle tre masse, variabile definita come gerarchia di massa dei neutrini. Le oscillazioni dei neutrini solari hanno già permesso di determinare che , resta da determinare se o . Il primo caso () viene chiamato gerarchia normale (in questa configurazione le masse dei neutrini sarebbero ordinate come le masse misurate dei quark), il secondo gerarchia inversa. Per determinare univocamente il valore di ognuno dei tre autostati di massa dei neutrini è quindi necessario misurare la gerarchia di massa oltre al suo valore assoluto ottenibile con una misura diretta.
Riassumendo quanto detto prima: la misura della massa dei neutrini è uno degli obiettivi principali della fisica delle alte energie, le oscillazioni di neutrini hanno dimostrato che la massa non è nulla ma non sono in grado di fornire valori assoluti. Per questi servono misure dirette, che però non saranno in grado di ricostruire le singole masse dei tre neutrini. Per ottenere queste informazioni sarà necessario combinare le informazioni delle misure dirette e delle oscillazioni, queste ultime hanno già misurato molti parametri, il parametro mancante è la gerarchia di massa.
Approcci Sperimentali
[modifica | modifica wikitesto]Sperimentalmente la determinazione della gerarchia di massa si traduce nella misura del segno di , (), che può assumere i valori di +/- 1, in corrispondenza della gerarchia normale ed inversa, rispettivamente. Le oscillazioni nel vuoto dei neutrini muonici, non sono in grado di determinare perché ogni termine che dipende da si trova nella forma [5], e quindi ogni dipendenza da viene persa.
Sono comunque possibili almeno tre approcci per misurare la gerarchia di massa:
- Le oscillazioni nella materia[6], a differenza delle oscillazioni nel vuoto, sono sensibili a e quindi gli esperimenti long-baseline (esperimenti agli acceleratori a lunghe distanze), dove i neutrini attraversano lunghi tragitti nella materia, possono misurare la gerarchia di massa. Gli esperimenti attuali, T2K e NOvA[7] , non hanno comunque sufficiente sensibilità per decidere quale sia la gerarchia di massa. Gli esperimenti di nuova generazione, DUNE[8] e Hyper-Kamiokande, saranno in grado di determinare con grande significanza statistica la gerarchia di massa. Queste misure sono rese difficili dal fatto che gli effetti di materia contribuiscono marginalmente alla probabilità totale di oscillazione, con frazioni fra il 5% e il 15% a seconda della configurazione. Gli effetti indotti dalle oscillazioni nella materia avvengono inoltre ad energie simili a quelli indotti dagli effetti di CP, e producono effetti simili. Per questo motivo gli esperimenti di nuova generazione dovranno misurare con precisione l'energia dei neutrini per poter distinguere gli effetti di materia dagli effetti di violazione di CP, e quindi misurare senza ambiguità sia che ẟCP.
- Misure di scomparsa di antineutrini dell'elettrone generati da reattori nucleari. Se queste vengono effettuate al massimo di oscillazione, quindi al valore di L/E delle oscillazioni solari: , sono in grado di misurare la gerarchia di massa attraverso l'interferenza dei termini solari ed atmosferici, come proposto inizialmente da Choubey et al. nel 2003[9]. Questo è il tipo di misura seguito dall'esperimento JUNO[10][11] in Cina, che si prevede che comincerà la presa dati nel 2025. La difficoltà di questo approccio è l'estrema risoluzione energetica richiesta per poter identificare la gerarchia di massa. JUNO dovrà raggiungere la risoluzione energetica del 3% (ad 1 MeV) per misurare la gerarchia di massa, risoluzione mai ottenuta dai precedenti esperimenti di neutrini a scintillatore liquido (molto più piccoli). La sensibilità potrebbe migliorare se i futuri esperimenti di oscillazione forniranno misure più precise di , come discusso in [12].
- I neutrini atmosferici possono attraversare tutta la Terra prima di arrivare al rivelatore. Come discusso la prima volta da S. Petcov nel 1998 [13] (si veda anche Akhmedov et al. 2013[14]), esistono effetti di risonanza delle oscillazioni particolarmente importanti ad angoli zenitali cos(θz) compresi fra -0.6 e -0.8 (dove i neutrini attraversano il nucleo terrestre) ed energie comprese fra 4 e 8 GeV, dove la gerarchia di massa induce differenze misurabili di oscillazione fra neutrini ed antineutrini. Questo permette a Telescopi di Neutrini come IceCube, Orca[15] e Hyper-Kamiokande di misurare la gerarchia di massa. Queste misure sono rese difficili dal fatto che i Telescopi di Neutrini non sono in grado di distinguere i neutrini dagli antineutrini (e devono ricorrere ad effetti secondari come le differenze fra le sezioni d'urto per separarli) e devono comunque raggiungere risoluzioni energetiche accettabili per misurare gli effetti.
La misura della gerarchia di massa dei neutrini è quindi uno degli scopi principali della prossima generazione di esperimenti di oscillazione dei neutrini e rimane una misura fondamentale per chiarire il problema del valore delle masse dei neutrini. È comunque una sfida sperimentale per gli esperimenti di prossima generazione.
Note
[modifica | modifica wikitesto]- ^ (EN) The Nobel Prize in Physics 2015, su NobelPrize.org.
- ^ Marco Galeota, Premio Nobel per la Fisica 2015, su Laboratori Nazionali del Gran Sasso, 2015. URL consultato l'8 maggio 2024.
- ^ Francesco Vissani, Con passo leggero, su Asimmetrie, 2013. URL consultato l'8 maggio 2024.
- ^ (EN) Particle Data Group, su Particle Data Group.
- ^ (EN) Carlo Giunti e Chung W. Kim, Fundamentals of Neutrino Physics and Astrophysics, Oxford University Press, 15 marzo 2007, DOI:10.1093/acprof:oso/9780198508717.001.0001, ISBN 978-0-19-170886-2.
- ^ (EN) Mikheyev, S. P. e Smirnov, A. Yu., Resonance Amplification of Oscillations in Matter and Spectroscopy of Solar Neutrinos, in Sov. J. Nucl. Phys., vol. 42, 1985, p. 913--917.
- ^ (EN) NOvA, su novaexperiment.fnal.gov. URL consultato il 9 maggio 2024.
- ^ (EN) Deep Underground Neutrino Experiment, su dunescience.org. URL consultato il 9 maggio 2024.
- ^ (EN) Sandhya Choubey, S. T. Petcov e M. Piai, Precision neutrino oscillation physics with an intermediate baseline reactor neutrino experiment, in Physical Review D, vol. 68, n. 11, 30 dicembre 2003, pp. 113006, DOI:10.1103/PhysRevD.68.113006.
- ^ (EN) Jiangmen Underground Neutrino Observatory, su juno.ihep.cas.cn. URL consultato il 9 maggio 2024.
- ^ JUNO collaboration, Potential to Identify the Neutrino Mass Ordering with Reactor Antineutrinos in JUNO, in arXiv, vol. 2405.18008.
- ^ (EN) Hiroshi Nunokawa, Stephen Parke e Renata Zukanovich Funchal, Another possible way to determine the neutrino mass hierarchy, in Physical Review D, vol. 72, n. 1, 29 luglio 2005, pp. 013009, DOI:10.1103/PhysRevD.72.013009.
- ^ S.T. Petcov, Diffractive-like (or parametric-resonance-like?) enhancement of the Earth (day-night) effect for solar neutrinos crossing the Earth core, in Physics Letters B, vol. 434, n. 3-4, 1998-08, pp. 321–332, DOI:10.1016/s0370-2693(98)00742-4.
- ^ (EN) E. Kh. Akhmedov, Soebur Razzaque e A. Yu. Smirnov, Mass hierarchy, 2-3 mixing and CP-phase with huge atmospheric neutrino detectors, in Journal of High Energy Physics, vol. 2013, n. 2, 14 febbraio 2013, pp. 82, DOI:10.1007/JHEP02(2013)082.
- ^ (EN) S. Aiello, et al., Determining the neutrino mass ordering and oscillation parameters with KM3NeT/ORCA, in The European Physical Journal C, vol. 82, n. 1, 2022, pp. 26, DOI:10.1140/epjc/s10052-021-09893-0.
Collegamenti esterni
[modifica | modifica wikitesto]- (EN) massive-neutrino hypothesis, su Enciclopedia Britannica, Encyclopædia Britannica, Inc.