Kerékgráf

Kerékgráf
Példák kerékgráfokra
Csúcsok száma	n
Élek száma	2(n − 1)
Átmérő	2, ha n>4 1, ha n=4
Derékbőség	3
Kromatikus szám	3, ha n páratlan 4, ha n páros
Spektrum	$\{2\cos(2k\pi /(n-1))^{1};$ $k=1,\ldots ,n-2\}$$\cup \{1\pm {\sqrt {n}}\}$
Egyéb	Hamiltoni Önduális Síkgráf
Jelölés	Wn

A matematika, azon belül a gráfelmélet területén egy kerékgráf (wheel graph) olyan gráf, amit egy körgráf univerzális csúccsal való bővítésével kapunk. Az n csúcsú kerékgráf tekinthető az (n−1)-szögű gúla 1-vázának is. Egyes szerzők W_n-nel jelölik az n csúcsú (n ≥ 4) kerékgráfokat; más szerzők viszont az n „küllőjű”, azaz n+1 csúcsú (n ≥ 3) kerékgráfot jelölik W_n-nel. Ebben a szócikkben a két jelölés közül az elsőt használjuk.

Konstrukció

Az {1,2,3,…,v} csúcshalmazt tekintve a kerékgráf élhalmaza a következő felsorolással adható meg: {{1,2},{1,3},…,{1,v},{2,3},{3,4},…,{v-1,v},{v,2}}.

Tulajdonságai

A kerékgráfok síkgráfok, továbbá Halin-gráfok. Önduálisak: bármely kerékgráf duálisa egy vele izomorf gráf. Minden maximális síkgráf részgráfként tartalmazza vagy a W₅, vagy a W₆ kerékgráfot; a K₄ = W₄ esettől eltekintve.

A kerékgráf mindig tartalmaz Hamilton-kört, továbbá a W_n-ben pontosan $n^{2}-3n+3$ kör található (A002061 sorozat az OEIS-ben).

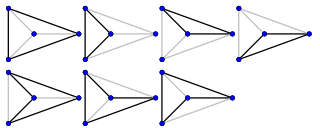A W4 kerékgráf 7 köre.

Páratlan n-ekre a W_n perfekt gráf, kromatikus száma 3: a kör szélén lévő csúcsok váltakozva két színnel színezhetők, a közepének pedig egy harmadik színt kell adni. Páros n-ekre a W_n kromatikus száma 4, és (ha n ≥ 6) nem perfekt. A W₇ az egyetlen kerékgráf, ami az euklideszi síkon egységtávolsággráf.

A W_n kerékgráf kromatikus polinomja:

$P_{W_{n}}(x)=x((x-2)^{(n-1)}-(-1)^{n}(x-2)).$

A matroidok elméletében a „kerékmatroidok” (wheel matroids) és az „örvénymatroidok” (whirl matroids) két különösen fontos matroidosztályt alkotnak – mindkettő a kerékgráfokból származik. A k-kerék matroid a W_k+1 kerék grafikus matroidja, míg a k-örvény matroid a k-kerékből származik, ha a kerék külső körét és annak összes feszítőfáját függetlennek tekintjük.

A W₆ kerékgráf Erdős Pál egy Ramsey-elméleti sejtésére szolgáltatott ellenpéldát: Erdős úgy sejtette, hogy az azonos kromatikus számú gráfok közül a teljes gráfnak legkisebb a Ramsey-száma, de Faudree és McKay (1993) megmutatták, hogy a W₆ Ramsey-száma 17, míg a vele azonos kromatikus számú K₄ teljes gráf Ramsey-száma 18. Tehát bármely 17 csúcsú G gráf esetében vagy G-nek vagy a komplementerének tartalmaznia kell a W₆-t részgráfként, míg például sem a 17 csúcsú Paley-gráf, sem a komplementere nem tartalmaz K₄-et.

Fordítás

• Ez a szócikk részben vagy egészben a Wheel graph című angol Wikipédia-szócikk ezen változatának fordításán alapul. Az eredeti cikk szerkesztőit annak laptörténete sorolja fel. Ez a jelzés csupán a megfogalmazás eredetét és a szerzői jogokat jelzi, nem szolgál a cikkben szereplő információk forrásmegjelöléseként.