Patróns de moiré

En física, matemáticas, arte e artes gráficas os patróns moiré ou de moiré son uns patróns de interferencia que ocorren cando se pode atopar un patrón opaco con ocos ou baleiros transparentes sobre outro patrón semellante. Para que apareza tal interferencia, os dous patróns non deben de ser completamente idénticos, senón estaren máis ben desprazados, rotados ou cun ton lixeiramente diferentes.

• 
  Efecto moiré cando superposición de dous patróns de puntos do mesmo ton, pero desprazados

As liñas poden ser as fibras dun tecido de moiré (as que lle dan nome ao efecto), liñas simples na pantalla do ordenador, ou en acetatos, en liñas de varas etc. O sistema visual humano crea a ilusión de bandas escuras e claras que se superpoñen ás liñas finas que realmente forman o trazado.

• 
  Patrón de Moiré que aparece nas capturas de pantalla LCD
• 
  Detalle dun micrómetro
• 
  A distancia entre os dous valados da ponte crea o patrón moiré.

Estes patróns aparecen en situacións moi diversas. Na impresión sobre papel ou outros soportes, o patrón en puntos pode interferir coa imaxe. Na foto dixital e na televisión, o patrón dun obxecto fotografado pode interferir coa forma dos sensores de luz e xerar artefactos non desexados. Ás veces pódense crear deliberadamente: en micrómetros (instrumentos de medida) úsanse para amplificar efectos de movementos moi pequenos. Tamén se poden formar patróns complexos superpoñendo figuras de liñas curvas e entrelazadas.

• 
  As liñas que forman o ceo crean patróns cando se mostran nalgunhas resolucións.
• 
  Moiré ben visible nesta fotografía das plumas dun papagaio (máis pronunciado na imaxe a tamaño completo)
• 
  Moiré visto nunha gaiola no zoo de San Francisco
• 
  Patrón de Moiré visto nun reloxo dixital
• 
  Dous conxuntos de paralelas, inclinados 5º entre si.
• 
  Moiré na porta dun garaxe.]]
• 
  Efecto de moiré nos ladrillos.

Os patróns de moiré poden considerarse 'artefactos' no contexto de gráficos por computadora e de infografías, xa que poden aparecer durante o proceso de captura dunha imaxe dixital (por exemplo, durante a dixitalización ou escaneo dunha imaxe con moito detalle) ou durante a xeración dunha imaxe sintética en 3D.

Produto de dúas «pistas de bips» de velocidades lixeiramente diferentes, que superpostas producen un patrón de moiré acústico (ver: phase music)

En física, a súa manifestación é a interferencia de ondas como a que se ve no experimento de dobre fenda e o fenómeno da batida acústica. Os patróns de moiré tamén poden ser útiles no contexto do estudo da fatiga material. Unha reixa obtida a partir dun material intacto pode superpoñerse a outra obtida a partir do mesmo material baixo tensión e grazas aos patróns de moiré pódense facer pequenos cambios, xa que o patrón de moiré é moito máis ostensíbel do que as diferenzas elásticas do material.

Etimoloxía

O termo orixínase na palabra francesa moiré (pronunciado [mwaˈʀe] ), un tipo de téxtil, tradicionalmente seda pero tamén de algodón ou fibra sintética, cun aspecto ondulado ou regado. O moiré, ou «téxtil regado», faise premendo dúas capas de téxtil cando está mollado. A disposición similar pero non exactamente coincidente dos fíos crea un patrón característico que permanece ao secar o tecido.

• 
  Tecido de moiré
• 
  Pedro o Grande cunha banda de moiré.

En francés, o adxectivo moiré (documentado desde 1823) deriva do verbo "moirer", que á súa vez é unha variación do inglés mohair (en uso desde 1570). Mohair provén do árabe mukhayyar (مُخَيَّر, lit. "escollido"), pano feito coa lan da cabra de Angora, que se entende no sentido de "pano excelente ".

A formación do moiré

Os patróns de moiré adoitan seren imaxes producidas accidentalmente ou a propósito por varias técnicas de imaxe dixital e gráficos por computadora, por exemplo cando se escanea unha imaxe de semitón ou un patrón de raios dun plano a cadros (este último é un caso especial de aliasing). Isto pódese superar no mapeo de texturas empregando mapas MIP e filtrado anisotrópico.

• 
  Imaxe que mostra como os mapas MIP reducen o aliasing a longas distancias. Vexa o patrón de moire na imaxe da esquerda

As liñas poderían representar fibras da seda moiré, ou liñas debuxadas en papel, ou nun monitor. A interacción non lineal dos patróns ópticos crea un patrón real e visible de bandas escuras e claras aproximadamente paralelas, superposto ás liñas.

O efecto moiré tamén se produce entre obxectos transparentes ou translúcidos superpostos. Por exemplo, unha máscara de fase invisible consiste nun polímero transparente cun perfil de espesor ondulado. A medida que a luz pasa a través de dúas máscaras superpostas de patróns de fase similares, prodúcese un amplo patrón de moiré nun ecrán ou pantalla a determinada distancia. Este efecto de fase e máis o clásico efecto moire de liña opaca son dous extremos dun espectro continuo en óptica, chamado efecto moiré universal .

• 
  Liña de Moiré cun movemento lento da capa de desenvolvemento cara arriba
• 
  Patrón de Moiré creado superpoñendo dous conxuntos de círculos concéntricos
• 
  Figura de Moiré
• 
  Curvas de Moiré modificando os patróns das capas
• 
  interferencias variando co xiro entre 0º e 6º.

O efecto moiré de fase é a base dun tipo de interferómetro de banda ancha en aplicacións de raios X e ondas de partículas, que tamén ofrece un xeito de revelar patróns ocultos en capas invisibles.

Liña Moiré

É un tipo de patrón que aparece cando se superpoñen dúas capas transparentes con patróns opacos correlacionados. É o caso cando os patróns superpostos comprenden liñas rectas ou curvas. Ao mover a capa, os patróns transfórmanse ou móvense a unha velocidade máis rápida. Este efecto chámase aceleración óptica moiré. Créanse patróns de liña moiré máis complexos se as liñas son curvas ou non son exactamente paralelas.

Figura de moiré

É un tipo de patrón que demostra o fenómeno do moiré ascendente. A figura 1D é o caso particular simplificado da figura 2D. Os patróns unidimensionais poden aparecer cando unha capa opaca con pequenas liñas horizontais transparentes se superpón sobre outra que contén unha forma complexa repetida periodicamente no eixo vertical. Os patróns de moiré que revelan figuras complexas ou secuencias de símbolos nunha das capas (na maneira de formas comprimidas repetidas periodicamente) créanse con figuras de moiré, tamén chamadas patróns de bandas de moiré. Unha das propiedades máis importantes da figura de moiré é a súa capacidade para aumentar pequenas formas ao longo dun ou ambos eixes, é dicir, de estirarse. Un exemplo 2D común de aumento de moiré ocorre cando se visualiza unha malla metálica a través dunha segunda malla de deseño idéntico. A fina estrutura do deseño pódese ver mesmo a grandes distancias.

Redución do patrón moiré

Varios patróns de moiré segundo a relación entre os píxeles e os puntos da imaxe inicial (retrato de Sarah Bernhardt de Felix Nadar, 1864)

É posible reducir o patrón de moiré aplicando filtros ou con algúns trucos. Nas dixitalizacións de documentos pódense limitar xirando a imaxe. Debido a que xa non se fai nos mesmos eixes, pódese reducir ou amplificar o efecto. A filtración cun filtro gaussiano limita o patrón sen erradicalo por completo. Resultados similares tamén se poden obter cun filtro medio .

Os drivers dos escáneres adoitan ter a opción de eliminar o moiré. O método habitual é ampliar a imaxe mediante interpolación e aplicar un desenfoque gaussiano nesta versión sobre-mostrada. Despois pódese reducir o tamaño da imaxe para que as dimensións coincidan co orixinal. Tamén se pode aplicar un filtro de "acento" para resaltar os detalles.

Un filtrado máis avanzado aproveita o feito de que o patrón de moiré ten algunha frecuencia cun predominio nun eixo particular. Cos filtros de paso de banda, é posible eliminar do espectro as frecuencias relacionadas co moiré. Non obstante, este problema segue a ser difícil na práctica porque o fenómeno é a miúdo non lineal (imaxes dun sistema analóxico) ou perturbado polo ruído.

Cálculos

Patróns de moiré paralelos

Enfoque xeométrico

Sexan dous patróns feitos de liñas paralelas e equidistantes, por exemplo, liñas verticais. A distancia entre liñas do primeiro patrón é p, e do segundo patrón é p + δp, con 0 < δp < p. Se as liñas dos patróns se superpoñen á esquerda da figura, o desprazamento aumenta a medida que se vai á dereita. Despois dun determinado número de liñas, os patróns opóñense: as liñas do segundo patrón atópanse entre as do primeiro patrón. Se se mira de lonxe, tens a sensación de áreas pálidas cando as liñas se superpoñen (hai branco entre as liñas) e áreas escuras cando as liñas son "opostas" .

• 
  Os patróns superpoñen a parte media da figura
• 
  Moire obtido superpoñendo dous patróns similares xirados por un ángulo

O centro da primeira zona escura é cando o desprazamento é igual a p/2 . A n liña do segundo patrón móvese por n δp en comparación coa n liña do primeiro patrón. Isto corresponde á metade da primeira zona escura.$$n\cdot \delta p={\frac {p}{2}}$$

Isto é,$$n={\frac {p}{2\delta p}}.$$A distancia d está entre unha zona pálida e unha zona escura$$d=n\cdot (p+\delta p)={\frac {p^{2}}{2\delta p}}+{\frac {p}{2}}$$a distancia entre o medio de dúas zonas escuras, que tamén é a distancia entre dúas zonas pálidas, é$$2d={\frac {p^{2}}{\delta p}}+p$$Desta fórmula pode verse que:

• canto maior é a distancia entre liñas, maior é a distancia entre áreas pálidas e escuras;
• canto maior é a discrepancia δp, máis próximas son as zonas escuras e claras; un grande espazo entre ambas significa que os patróns teñen moi pequenas as distancias entre as liñas.

O principio do moiré é similar á escala de Vernier.

Enfoque con funcións matemáticas

A esencia do efecto é a sensación (principalmente a percepción visual) dun terceiro patrón distinto causado pola superposición imprecisa de dous motivos similares. A representación matemática destes patróns non se obtén de xeito trivial. Nesta sección daremos un exemplo matemático de dous patróns paralelos cuxa superposición forma un patrón moiré e amosaremos dun xeito (de moitas maneiras posíbeis) de que estes patróns e o efecto moiré poidan representarse matematicamente.

Patrón de moiré (abaixo) creado superpoñendo dúas cuadrículas (arriba e medio)

A visibilidade destes patróns depende do soporte ou substrato sobre o que aparezan e poden ser opacas (coma no papel ) ou transparentes (como nunha película de plástico). Para o debate, imos supoñer que os dous patróns principais están impresos en tinta de escala de grises nunha folla branca, onde a opacidade (por exemplo, tonalidade gris) da parte impresa vén dada por un valor entre 0 (branco) e 1 ( negro) incluído, con 1/2 representando o gris neutro. Calquera valor inferior a 0 ou superior a 1 que use esta escala de grises é esencialmente «non imprimible».

Tamén elixiremos representar a opacidade do patrón resultante de imprimir un patrón encima do outro nun determinado punto do papel como a media (é dicir, a media aritmética ) da opacidade de cada patrón nesta posición, que é a metade da súa suma e, segundo o cálculo, non supera 1 (esta opción non é única. Tamén servirá calquera outro método para combinar funcións que satisfaga manter o valor da función resultante dentro dos límites [0,1]; a media aritmética ten a virtude da simplicidade, co menor dano posible nos conceptos do proceso de gravación).

Agora consideramos a "impresión" da superposición de dous patróns de escala de grises case similares, que varían sinusoidalmente, para amosar como producen un efecto moiré imprimindo primeiro un patrón no papel e logo imprimindo o outro patrón no primeiro, mantendo o seu eixe de coordenadas no rexistro. Representamos a intensidade gris de cada patrón por unha función de opacidade de distancia positiva ao longo dunha dirección fixa (por exemplo, a coordenada x) no plano do papel, na forma$$f={\frac {1+\sin(kx)}{2}}$$ onde a presenza de 1 mantén a función positiva definida e a división por 2 impide valores de función superiores a 1.

A cantidade k representa a variación periódica (é dicir, a frecuencia espacial) da intensidade gris do patrón, medida como o número de ciclos de intensidade por unidade de distancia. Dado que a función seno é cíclica por encima dos cambios de argumentos de 2π, o aumento da distancia Δx por ciclo de intensidade (a lonxitude de onda ) obtense cando k Δx = 2π, ou Δx = 2π/k .

Imos considerar agora estes dous patróns, nos que un ten unha variación periódica lixeiramente diferente do outro:$${\begin{aligned}f_{1}&={\frac {1+\sin(k_{1}x)}{2}}\\[4pt]f_{2}&={\frac {1+\sin(k_{2}x)}{2}}\end{aligned}}$$tal que k₁ ≈ k₂ .

A media destas dúas funcións, que representa a imaxe impresa superposta, avalíase do seguinte xeito:$${\begin{aligned}f_{3}&={\frac {f_{1}+f_{2}}{2}}\\[5pt]&={\frac {1}{2}}+{\frac {\sin(k_{1}x)+\sin(k_{2}x)}{4}}\\[5pt]&={\frac {1+\sin(Ax)\cos(Bx)}{2}}\end{aligned}}$$onde se demostra facilmente que$$A={\frac {k_{1}+k_{2}}{2}}$$e$$B={\frac {k_{1}-k_{2}}{2}}.$$Esta función media, f₃, está claramente no rango [0,1]. Dado que a variación periódica A é a media e, polo tanto, próxima a k₁ e k₂, o efecto moiré demóstrase de maneira distintiva pola función "latexo" da envoltura do cos(Bx) sinusoidal cos(Bx), cuxa variación periódica é a metade da diferenza das variacións periódicas k₁ e k₂ (e, obviamente, moito menor en frecuencia).

Outros efectos moiré unidimensionais inclúen o clásico latexo do ton de frecuencia que se escoita cando dúas notas puras de ton case idéntico soan simultaneamente. É unha versión acústica do efecto moiré na única dimensión do tempo: as dúas notas orixinais seguen presentes, pero a percepción do oínte é de dous tons que son a diferenza da media das frecuencias das dúas notas. O aliasing na mostraxe de sinais que varían no tempo tamén pertence a este paradigma moiré.

Enfoque sinusoidal

Se xa non consideramos patróns de liñas de alto contraste, senón patróns transparentes con contraste $\mathrm {I}$ que varían continuamente de xeito sinusoidal

$\mathrm {I} _{1}(x)=\mathrm {I} _{0}\cdot \sin(2\pi \cdot k_{1}\cdot x)$

$\mathrm {I} _{2}(x)=\mathrm {I} _{0}\cdot \sin(2\pi \cdot k_{2}\cdot x)$

(os pasos son respectivamente p ₁ = 1 / k ₁ e p ₂ = 1 / k ₂ ), a intensidade cando os dous patróns se superpoñen é entón

$\mathrm {I} (x)=\mathrm {I} _{0}\cdot (\sin(2\pi \cdot k_{1}\cdot x)+\sin(2\pi \cdot k_{2}\cdot x))$

ou, segundo a fórmula da suma de dous senos derivados das fórmulas de Euler:

$\mathrm {I} (x)=\mathrm {I} _{0}\cdot 2\cos \left(2\pi {\frac {(k_{1}-k_{2})}{2}}\cdot x\right)\cdot \sin \left(2\pi {\frac {(k_{1}+k_{2})}{2}}\cdot x\right)$

• 
  A interferencia de localización latexa nun momento dado, cunha diferenza de lonxitude de onda do 1%
• 
  Superposición de dous patróns con densidade de gris sinusoidal de lonxitude de onda lixeiramente diferente

Polo tanto, pódese ver que a intensidade resultante consiste nun sinusoide que ten unha alta " frecuencia espacial " (número de onda) que é a media das frecuencias espaciais dos dous patróns e unha sinusoide cunha frecuencia espacial.

Baixa que é a metade a diferenza nas frecuencias espaciais dos dous patróns. Este segundo compoñente é un "envoltorio" para o outro sinusoide. A lonxitude de onda λ deste compoñente é a inversa da frecuencia espacial

${\frac {1}{\lambda }}={\frac {k_{1}-k_{2}}{2}}={\frac {1}{2}}\cdot \left({\frac {1}{p_{1}}}-{\frac {1}{p_{2}}}\right)$

se o poñemos p ₁ = p e p ₂ = p + δ p :

$\lambda =2{\frac {p_{1}p_{2}}{p_{2}-p_{1}}}\Leftrightarrow {\frac {\lambda }{2}}={\frac {p^{2}}{\delta p}}+p$ .

Os ceros desta envoltura están espazados λ / 2 e os máximos de amplitude en valor absoluto están igualmente espazados λ / 2; polo tanto, atopamos o resultado do enfoque clásico. Este fenómeno é similar á estroboscopia temporal ou á produción de ritmos sonoros.

Rotación do patrón

Consideremos dous patróns coa mesma distancia entre as liñas p, pero o segundo patrón xira un ángulo α . Visto de lonxe, tamén podemos ver liñas máis escuras e claras: as liñas máis claras corresponden ás liñas de nodos, é dicir, as liñas que pasan polas interseccións dos dous patróns.

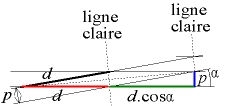
Se considerarmos unha cela da rede formada, poderemos ver que é un rombo cos catro lados iguais a d = p/sin α ; (temos un triángulo rectángulo cuxa hipotenusa é d e o lado oposto ao ángulo α é p ).

• 
  Unidade de cela da "rede" ; "Ligne claire" significa "liña clara"
• 
  Efecto do cambio de ángulo

As liñas claras corresponden á pequena diagonal do rombo. Dado que as diagonais son as mediatrices dos lados veciños, podemos ver que a liña pálida fai un ángulo igual a α/2 coa perpendicular da liña de cada patrón. Ademais, o espazo entre dúas liñas claras é D, a metade da longa diagonal. A longa diagonal 2D é a hipotenusa dun triángulo rectángulo e os lados do ángulo recto son d(1 + cos α) e p . O teorema de Pitágoras dá:$$(2D)^{2}=d^{2}(1+\cos \alpha )^{2}+p^{2}$$isto é:$${\begin{aligned}(2D)^{2}&={\frac {p^{2}}{\sin ^{2}\alpha }}(1+\cos \alpha )^{2}+p^{2}\\[5pt]&=p^{2}\cdot \left({\frac {(1+\cos \alpha )^{2}}{\sin ^{2}\alpha }}+1\right)\end{aligned}}$$así$${\begin{aligned}(2D)^{2}&=2p^{2}\cdot {\frac {1+\cos \alpha }{\sin ^{2}\alpha }}\\[5pt]D&={\frac {\frac {p}{2}}{\sin {\frac {\alpha }{2}}}}.\end{aligned}}$$

• 
• 
• 

Cando α é moi pequeno ( α < π/6 ) pódense facer as seguintes aproximacións para pequenos ángulos: $${\begin{aligned}\sin \alpha &\approx \alpha \\\cos \alpha &\approx 1\end{aligned}}$$así$$D\approx {\frac {p}{\alpha }}.$$Podemos ver que canto menor α, é dicir, canto máis lonxe están as liñas claras; cando os dous patróns son paralelos ( α = 0 ), o espazo entre as liñas claras é infinito (non hai ningunha liña clara). Polo tanto, hai dúas formas de determinar α : pola orientación das liñas claras e pola súa separación$$\alpha \approx {\frac {p}{D}}$$Se decidirmos medir o ángulo, o erro final é proporcional ao erro de medición. Se o que se decide medir é a separación, o erro final é proporcional á inversa da separación. Polo tanto, para pequenos ángulos, é mellor medir a separación.

Implicacións e aplicacións

Impresión de imaxes a toda cor

En artes gráficas e preimpresión, a tecnoloxía habitual para imprimir imaxes a toda cor implica a superposición de pantallas de semitón. Estes son patróns regulares de puntos rectangulares, moitas veces catro, impresos en ciano, amarelo, maxenta e negro. Algúns patróns de moiré son inevitables, pero en circunstancias favorables o patrón está "axustado"; é dicir, a frecuencia espacial do mouré é tan alta que non se nota.

• 
  x
• 
  Exemplos de ángulos de pantalla CMYK de semitonos típicos
• 
  Este primeiro plano dunha impresión de semitonos mostra como o maxenta na parte superior do amarelo aparece como laranxa / vermello e o cian na parte superior do amarelo aparece como verde.

Nas artes gráficas, o termo moiré significa un patrón excesivamente visible de moiré. Parte da preimpresión é seleccionar ángulos de pantalla e frecuencias de semitonos que minimizan o moiré. A visibilidade do moiré non é totalmente predicíbel. O mesmo conxunto de pantallas pode producir bos resultados con algunhas imaxes, pero moiré visíbel con outras.

Móbil, Eusebio Sempere, 1972; escultura ao aire libre explorando o efecto moiré (Madrid)

Tamén hai obras de artistas que usan o efecto dun xeito buscado e deliberado, en especial os do Op-Art, un vínculo entre as Matemáticas e a Arte

Pantallas de TV e fotografías

Os patróns de moiré vense normalmente nas pantallas de televisión cando unha persoa leva unha camisa ou chaqueta dun tecido ou patrón en particular. Isto débese á exploración entrelazada de televisores e cámaras non cinematográficas, coñecida como twister interline, a medida que a persoa se move, o patrón de moiré nótase bastante. Por esta razón, os medios de comunicación e outros profesionais que aparecen regularmente na televisión reciben instrucións para evitar a roupa que poida causar este efecto.

• 
  Efecto "pinta"
• 
  Demostración de dixitalización entrelazada e o chamado twister interline

As fotografías dunha pantalla de televisión tomadas cunha cámara dixital adoitan presentar patróns de moiré. Debido a que tanto a pantalla do televisor como a cámara dixital utilizan unha técnica de dixitalización para producir ou capturar imaxes con liñas de escaneo horizontais, os conxuntos de liñas en conflito provocan patróns de moiré. Para evitar o efecto, a cámara dixital pode orientarse cun ángulo de 30 graos respecto á pantalla do televisor.

Moiré dixital

Na cadea de procesamento dixital dunha imaxe, pode aparecer un patrón na fase de dixitalización ou na pantalla.

• 
  Este deseño de píxeles atópase nas pantallas LCD S-IPS. A> forma úsase para ampliar o cono da pantalla
• 
  Moire dobre: pantalla clara / escura e artefacto de dixitalización RGB
• 
  Filtro de mosaico Bayer

No primeiro caso, o patrón moiré aparece debido á interferencia entre o cadro do sensor ( escáner ou matriz ) e o do obxecto dixitalizado. No caso dos sensores de cor, tamén pode xerar efectos de cor nunha imaxe que normalmente falta.

No segundo caso, o patrón de moiré aparece debido á interferencia entre a matriz de píxeles da pantalla e o cadro do obxecto mostrado. Este problema é similar aos efectos de impresión de semitons analóxicos descritos anteriormente.

Navegación marítima

O efecto moire úsase en balizas costeiras chamadas "luces de Inogon", fabricadas por Inogon Licens AB, Suecia, para designar a ruta de viaxe máis segura para os buques con destino a portos deportivos, portos etc. Indica riscos subacuáticos (como tubos ou cables). O efecto moiré crea frechas que apuntan nunha liña imaxinaria que marca o perigo ou a liña de paso seguro; a medida que os navegantes pasan por riba da liña, as frechas do faro parecen converterse en bandas verticais antes de volver ás frechas que apuntan na dirección oposta. Un exemplo pódese atopar no Reino Unido, na beira leste de Southampton, fronte á refinaría de petróleo Fawley. Pódense usar balizas similares de efecto moiré para guiar aos mariñeiros cara ao punto central dunha ponte que se achega; cando o buque está aliñado coa liña central, vense liñas verticais. Nos aeroportos despréganse luces Inogon para axudar aos pilotos no chan a permanecer na liña central das pistas.

Medición da deformación

Véxase tamén: Mecánica do sólido deformábel, Teoría da tensión infinitesimal e Interferometria holográfica.

Nas industrias manufactureiras, estes patróns úsanse para estudar a deformación microscópica en materiais: deformando unha reixa con respecto a unha rede de referencia e medindo o patrón de moiré, pódense deducir niveis de tensión e patróns. Esta técnica é atractiva porque a escala do patrón moiré é moito maior que o flechado que o provoca, o que facilita a medición. O efecto moiré pódese usar na medición de deformacións: o operador só ten que debuxar un patrón sobre o obxecto e superpoñer o patrón de referencia ao patrón deformado do obxecto deformado.

Uso do efecto moiré na medida das deformacións: caso de tracción uniaxial (superior) e cisalla pura (inferior); as liñas dos patróns son inicialmente horizontais nos dous casos

Pódese obter un efecto similar superpoñendo unha imaxe holográfica do obxecto sobre o propio obxecto: o holograma é o paso de referencia e a diferenza co obxecto son as deformacións, que aparecen como liñas pálidas e escuras.

Tracción uniaxial

Considere unha parte de lonxitude l sobre a que se traza unha rede de pasos p, cuxas liñas son perpendiculares ao eixo de tracción.

Baixo tensión, a peza ten unha lonxitude l · (1 + ε), onde ε é a deformación (elongación relativa). O paso da rede convértese en p · (1 + ε), de onde se obtén δp = p · ε.

Vemos que o espazo entre dúas áreas escuras é:$2d={\frac {p}{\varepsilon }}$ polo tanto, este espazo permite determinar a deformación. Non obstante, a medición da distancia entre dúas áreas escuras é imprecisa, debido ao ancho dunha área. Podemos estar satisfeitos contando o número N de liñas escuras que vemos: sobre unha lonxitude l, temos

$N={\frac {l\cdot \varepsilon }{p}}$

é dicir

$\varepsilon =N\cdot {\frac {p}{l}}$

A precisión é a deformación que separa dúas aparicións de liñas, é dicir: $\Delta \varepsilon ={\frac {p}{l}}$

Cisalla pura

No caso da cisalla pura, é suficiente trazar unha rede perpendicular ás forzas de escisión. A rede da parte deformada xírase entón co ángulo de corte γ respecto á rede de referencia (a parte non deformada). En canto á tensión uniaxial, pódese satisfacer contando o número de liñas, sempre que γ sexa moi baixo, que a parte sexa rectangular e que as forzas sexan paralelas aos lados (as liñas claras son case paralelas aos lados da peza).

Se o ancho da peza (perpendicular ás forzas) é l, o número de liñas N é igual a:

$N=l/D=l\cdot \gamma /p$

é dicir: $\gamma =N\cdot {\frac {p}{l}}$ co erro do anterior

$\Delta \gamma ={\frac {p}{l}}$

Procesamento de imaxes

Algúns programas de escáner de imaxes por ordenador proporcionan un filtro opcional, chamado filtro "descreen", para eliminar os artefactos do patrón moire.

Desprazamento das liñas de moiré co desprazamento dun patrón con respecto a outro

Medición de pequenos desprazamentos

Consideramos un patrón fixado nunha parte, observado a través dunha retícula coa distancia entre liñas lixeiramente diferente, considerada fixa. Temos por tanto un patrón de moiré. A medida que se move a peza, tamén o fan as liñas escuras e claras do patrón de moire; para un desprazamento de δp, as liñas móvense por p, na dirección oposta ao movemento. Atopamos o comportamento do vernier. Polo tanto, temos un factor de amplificación de p / δp. Isto permite medir pequenos movementos e velocidades baixas.

Billetes

Moitos billetes aproveitan a tendencia dos escáneres a produciren moiré incluíndo deseños circulares ou ondulados, de xeito que aparece un patrón cando se escanea ou imprime, dificultando a súa falsificación.

Microscopía

Na microscopía de super resolución, o patrón moire pode usarse para obter imaxes cunha resolución superior ao límite de difracción, usando unha técnica coñecida como microscopía de iluminación estruturada.

Na microscopía de efecto túnel, as tiras de moiré aparecen se as capas atómicas superficiais teñen unha estrutura cristalina diferente á do cristal. Isto pode deberse, por exemplo, á reconstrución superficial do cristal ou cando hai unha fina capa dun segundo cristal na superficie (por exemplo, monocapa de grafeno, dobre capa de grafeno, Heteroestructura de Van der Waals de grafeno e hBN ( nitruro de boro hexagonal) ou nanoestruturas de bismuto e antimonio

En Microscopía eléctrica de Transmiss (MET ou TEM polo nome en inglés), as raias moiré traslacionais poden ser vistas como liñas paralelas formadas no contraste de imaxes TEM de contraste pola interferencia dos planos da rede cristalina difratante que se sobrepoñen e poden ter un espazo e / ou orientación diferente. A maioría das observacións de contraste moiré descritas obtéñense empregando imaxes TEM de contraste de fase de alta resolución. Con todo, de usarse a imaxe dun microscopio de varrido electrónico corrixido por aberración de gran angular de campo escuro anular  (HAADF-STEM), obtense unha interpretación máis directa da estrutura cristalina en termos de tipos e posicións de átomos.

Ciencia dos materiais e física da materia condensada

Na física da materia condensada, o fenómeno moiré adoita estar en materiais bidimensionais. O efecto prodúcese cando hai un desaxuste entre o parámetro de retícula (ou o ángulo da capa 2D) e o do substrato subxacente (ou outra capa 2D), como nas heteroestructuras de materiais 2D. O fenómeno explótase como un medio de enxeñaría da estrutura electrónica ou propiedades ópticas dos materiais, que algúns chaman materiais moire. A miúdo cambios significativos nas propiedades electrónicas ao torcer dúas capas atómicas e a posibilidade de aplicacións electrónicas levaron ao nome de twistronics neste campo. Un exemplo destacado atópase na dobre capa de grafeno retorcido, que forma un patrón de moiré e cun ángulo máxico particular presenta supercondutividade e outras importantes propiedades electrónicas.

• 
  Superposición das redes hexagonais do grafeno cultivado na superficie (111) do iridio
• 
  Patrón de Moiré xurdido da superposición de dúas cuadrículas de grafeno xiradas 4 °

Na ciencia dos materiais, exemplos coñecidos de contraste moiré son, por exemplo, láminas finas ou nanopartículas tipo MX (M = Ti, Nb ; X = C, N ) superpostas cunha matriz austenítica. As dúas fases, MX e a matriz, teñen unha estrutura cristalina cúbica centrada na cara e unha relación de orientación cubo sobre cubo. Non obstante, presentan un importante desaxuste de rede entre o 20 e o 24% (baseado na composición química da aliaxe ), o que produce un efecto moire.

Véxase tamén

Bibliografía

• Sincerbox, Glenn T. (1991). Counterfeit deterrent features for the next-generation currency design (en inglés). Washington, DC.: National Materials Advisory Board. ISBN 9780309050289. 
• Figueiredo, Mário; Zerubia, Josiane; Jain, Anil K., eds. (2001). Energy Minimization Methods in Computer Vision and Pattern Recognition (en inglés). Berlín: Springer. ISBN 3-540-42523-3. 
• Kazda, Antonín; Caves, Robert (2015). Airport design and operation (en inglés). Bingley, England: Emerald. ISBN 9781784418700. 
• Williams, David B.; Carter, C. Barry (2009). Transmission electron microscopy: a textbook for materials science (en inglés). Nova York / Londres: Springer. ISBN 9780387765013. OCLC 876600051. 

Ligazóns externas

• O patrón infinito que NUNCA se repite, vídeo de YouTube coa explicación dos patróns de Penrose en base ao efecto moiré (en inglés e castelán).
• Unha serie de pinturas ao óleo baseadas nos principios do patrón moire da artista británica Pip Dickens
• Unha demostración do efecto moire causado pola interferencia entre círculos Arquivado 26 de abril de 2021 en Wayback Machine.
• Un exemplo interactivo de varios patróns de moire
• Efecto moire de fase: patrón de moire nunha pantalla detrás de dúas máscaras de fase transparentes cando a pantalla se afasta
• Persoal descentrado en operadores de Laplacia
• The Moire Effect Lights That Guide Home Ships, un vídeo de YouTube Tom Scott, en luz Inogon Southampton (en inglés).